|
DER HARMONIK
Die harmonischen Typen des chromatischen
Systems, d.h.
sind dadurch charakterisiert, daß sie die Spannung der Fibonacci-Reihe mit der Geschlossenheit des Zwölftonsystems vereinigen. Die typischsten chromatischen Melodien und Harmonien von Bartók und Kodály gehorchen den Proportionen der Fibonacci-Sequenz. Zählt man Halbtöne, so bezeichnet
In Wirklichkeit drücken diese Zahlen
jedoch Proportionen aus, und nicht Halbtonschritte.
So wie Mozart und Haydn vor allem Dur- und Moll-Dreiklänge benutzten, und so wie wir uns an Septakkorde in der romantischen Musik gewöhnt haben, so wurde die Verwendung von auf die Fibonacci-Reihe gegründeten Harmonien in den Werken von Bartók und Kodály ebenfalls üblich und vorherrschend. Bsp. 26
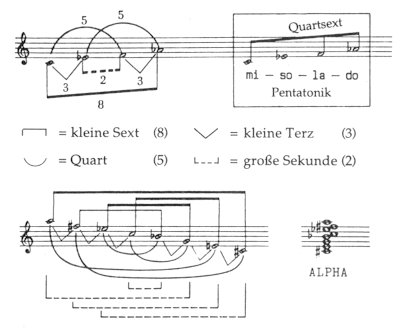
Wir benennen diesen Akkordtyp mit einer zusammenfassenden Bezeichnung als alpha-Harmonie; seine verschiedenen Ausschnitte können dann mit den Buchstaben beta, gamma, delta und epsilon unterschieden werden. Der alpha-Akkord besteht aus zwei Schichten. Um eine Tonart zu etablieren, müssen wenigstens zwei Noten vorhanden sein: der Grundton (hier c) und einer seiner Obertöne, d.h. die Quint (g) oder die große Terz (e). In diesem einfachen Fall verstärken g oder e das c – obwohl sowohl g als auch e in sich ”dominantische” Bedeutung haben. Der alpha-Typ hat einen stark tonalen, sogar funktionalen Charakter. Wenn Kodály z.B. in der Hauptkadenz seiner ”Anwerbung” (Háry) vor dem tonikalen E-Dur nach einem dominantischen alpha-Akkord sucht, dann gestaltet er dessen obere Schicht aus der Melodie selbst (h-gis-f-d) und dessen untere, begleitende Schicht aus dem verminderten Septakkord c-dis-fis-a: Bsp. 27
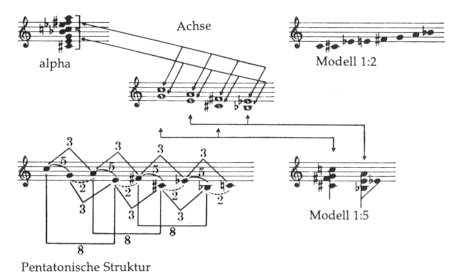
Damit ist der alpha-Typ nichts Geringeres als die ”Achsen”-Anpassung der einfachen Beziehung c-e-g oder c-g. Das Fehlen der Quint und großen Terz (g und e), das einen unstabilen Tonartcharakter bewirkt, ist auch der Grund, warum der Typ epsilon selten in Erscheinung tritt. Die einzige Bedingung für den alpha-Akkord ist, daß er aus zwei Schichten (zwei ”Achsen”) gebildet sein sollte. Der alpha-Typ erfüllt zwei Voraussetzungen. (1) Einerseits ist er aus der Pentatonik ableitbar; die Intervalle 2, 3, 5 und 8 (oder ihre Oktaven) erklingen überall im Akkord. Bsp. 28
Auf diese Weise erscheint in einem von Bartóks Chören das pentatonische DO-SO-LA-MI-Motiv in gamma- und delta-Harmonien verwandelt: Bsp. 29
(2) Andererseits sind alpha-Harmonien Achsen-Modelle und drücken als solche die polymodalen und polaren Spannungen des Achsensystems aus (siehe hierzu Bsp. 34.) Hier wäre hinzuzufügen: Die Spannung der alpha-Harmonien kann am einfachsten und effektvollsten durch die Symbole der Polymodalität ausgedrückt werden. Bsp. 30
Beispiele aus Bartóks Werken Bsp. 31
Durch die chromatische Gegenüberstellung der Intervalle
2, oder 3, oder 5 entstehen ”geschlossene” Tonleitern: bei periodischer
Wiederholung der Intervalle wird man zum Ausgangspunkt zurückgeführt.
Bsp. 32
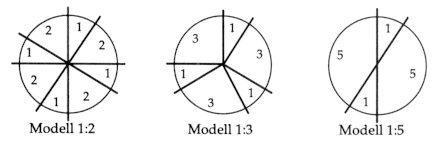
Das Modell 1:2 sollte als ”Grundtonleiter” des Achsensystems verstanden werden. Innerhalb des Zwölftonbereichs können drei verschiedene 1:2 Modelle aufgestellt werden, in Übereinstimmung mit den drei Funktionen: eine Tonika, eine Dominante und eine Subdominante. Jede weitere Version stimmt mit einem dieser Modelle überein; z.B. in C-Tonalität: Bsp. 33
Alle Akkorde und Modelle, die derselben Achse zugehören, konstituieren eine funktionale Einheit.
Die c-es-fis-a Achse*)
Beispiele aus Bartóks Werken Bsp. 35
Harmonische Wendungen innerhalb des Modells 1:2 **) Wenn wir einen Dur-Septakkord (z.B. c-e-g-b) mit eine kleine Terz höher liegenden Submoll-Akkord kombinieren, so erhalten wir das Modell 1:2. Diese Kombination wurde unter den Romantikern geläufig. Bsp. 36
Im ersten Akt des Tristan wird
die ”innere” Welt mit dem ”Tristan-Akkord” (f-submoll) verkörpert,
die ”äußere” Welt dagegen durch den Chor des Schiffsvolks, der
stets in der Form eines ”D-Dur-Septakkords” erscheint.
Bsp. 37
Das Modell 1:5 repräsentiert eine weitere typische Achsensequenz: es beruht auf polaren Beziehungen. Bsp. 38
Beispiele aus Bartóks Werken Bsp. 39
Das Modell 1:2 kann aus zwei 1:5 Modellen zusammengesetzt werden. Bsp. 40
Im Mikrokosmos-Stück Auf der Insel Bali spielen sowohl die linke als auch die rechte Hand 1:5-Modelle, die dann zusammen ein vollständiges 1:2 Modell ergeben. Bsp. 41
Die Schlußakkorde vereinigen diese vier Elemente: Bsp. 42
Im letzten Akkord sind zwei Dreiklänge miteinander verschmolzen: der Unterschied zwischen den beiden Dreiklängen durch sechs Vorzeichen bewirkt eine polare Spannung, und die beiden Dreiklänge verbinden sich zu einer perfekten alpha-Harmonie: Bsp. 43
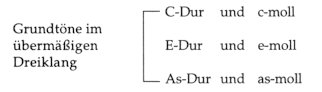
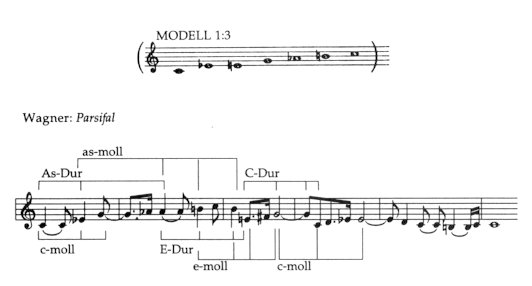
Während die Modelle 1:2 und 1:5 einen ausgeprägt ”tonalen” Charakter haben, hebt das 1:3 Modell das Gefühl für Tonalität auf. Dies geschieht aufgrund seiner auf dem übermäßigen Dreiklang fußenden Struktur. So beinhaltet z.B. das 1:3 Modell c-es-e-g-as-h die folgenden Dreiklänge:
Die ”schwebende” Eigenschaft des 1:3 Modells wurde schon von Liszt und Wagner erkannt.
Beispiele aus Bartóks Werken Bsp. 45
Komplementäre (einander aufhebende) Tonarten Ein 1:3 Modell kann kreiert werden, indem man ein Dur-Dreiklang mit dem eine Großterz tieferen Moll-Dreiklang verbindet. In diesem Fall neutralisiert der eine Dreiklang den anderen, da ihre Noten zusammengenommen ein 1:3 Modell ergeben. Dies ist auch der Grund, warum diese Akkorde als Ausdruck kontrastierenden Gehalts empfunden werden.
Die Idee der gegenseitigen ”Aufhebung” geht auf romantische Modelle zurück. Wenn Wotan im großen Monolog in der Walküre die Götterdämmerung prophezeit, evozieren seine Worte ”Das Ende! Das Ende!” E-Dur und c-moll Dreiklänge, die sich tonal gegenseitig zerstören.
Eine besonders merkwürdige Manifestation der Idee von gegenseitiger Aufhebung findet sich in Webern’s berühmter Reihe, in der zwei 1:3 Modelle verschmolzen sind: Bsp. 48
Z.B. übersetzt Kodály in seinem Chorwerk Die Alten den Leben-und-Tod-Symbolismus des Stückes in der Sprache der Musik mit Hilfe komplementärer Tonarten: G-Dur und es-moll, dann b-moll und D-Dur: Bsp. 49
Die gesamte tonale Anlage von Herzog Blaubarts Burg beruht auf derartigen komplementären Beziehungen. Fis-moll ist die Tonart der Nacht und C-Dur die des Lichts. C-Dur kann mit Hilfe der Tonart as-moll zerstört werden – daher ist die letztere mit dem Symbolismus des Todes assoziiert. Andererseits kann das fis-moll der Nacht durch B-Dur besiegt werden – und dieses wurde daher zum Symbol der Liebe. Zusammengenommen schließen die vier Dreiklänge alle Stufen der chromatischen Tonleiter ein: ”Licht” : c-e-g——————— ”Tod” : as-ces-es ”Nacht” : fis-a-cis —————— ”Liebe” : b-d-f Die Grundtonart in Kodálys Psalmus Hungaricus, a-moll, steht für Weinen, Flehen, Verzweiflung und Fluch. Das ”dénouement” innerhalb der Handlung, andererseits, findet in der komplementären Tonart Des=Cis-Dur statt. Die Aufgabe von Des-Dur ist es, vom Gewicht des Fluchs freizusprechen: ”Er nimmt der Seele alle, alle Erdennot”. Cis-Dur wird zu Tonart der Erhebung und Apotheose: ”Herrlich und jubelnd, mächtig hebst Du ihn hoch”. Komplementäre Tonarten können auch in versteckter Form auftreten. Das ”Sündenqualmotiv” des Parsifal hat einen quälenden Effekt, weil die authentische Sequenz (die Akkordfolge, die sich in authentischer Richtung am Quintenzirkel entlang bewegt) von komplementären Akkorden gefärbt wird: F-Dur und des-moll in Takt 1, Des-Dur und a-moll in Takt 2, usw. Bsp. 50
Geschlossene Sequenzen können jedoch
durch einfachere Mittel erzeugt werden, nämlich durch die Zusammensetzung
äquidistanter Skalen basierend auf den Fibonacci-Intervallen 2, 3,
5, 8. So entsteht
QUARTENAKKORDE**) Aufgrund der starken Volkslied-Einflüsse kommt es in Bartóks und Kodálys Werken besonders häufig vor, daß Themenbildung und Harmonisierung auf Quartenakkorden fußen. ”Die charakteristische Quartenhäufung in unseren alten Melodien regte uns zur Bildung von Quartenakkorden an; wir haben dabei die horizontale Sukzession in vertikale Simultaneität projiziert” schreibt Bartók in einem Artikel. Hier ist ein Beispiel, wie er in seinem Violinkonzert die quartenreiche Melodie in Quartenharmonik umwandelt: Bsp. 51
TONIKA/ANTITONIKA-BEZIEHUNGEN INNERHALB PENTATONISCHER SKALEN So stammen also Quartenakkorde in Bartóks
und Kodálys Kompositionen aus der Volksmusik, und in Übereinstimmung
mit diesem Volkslied-Einfluß machen sich auch in der Verbindung der
Quartenakkorde die inneren Gesetze der Pentatonik bemerkbar.
Bsp. 52
Im Beispiel unten ist das ”Tonika”-Modell durch die Quartenstufen c-f-b repräsentiert, das ”Antitonika”-Modell durch die Quartenstufen b-es-as. Bsp. 53
Die Anziehungskraft zwischen Tonika und Antitonika hat ihren Ursprung in der Kadenz SO-RE ® MI (DO-SO ® LA), die in der Volksliedmelodik so häufig ist: SO-RE hält die Spannung aufrecht, während MI der Auflösung in die Tonika entspricht: Bsp. 54
Die Tatsache, daß wir es hier mit einem Zwei-Funktionen-System (und nicht, wie in der klassischen Harmonik, mit einem Drei-Funktionen-System) zu tun haben, verdient besondere Aufmerksamkeit. Übrigens haben Akkorde, die auf der Struktur SO-LA-DO-RE basieren, eine schwebende, emporstrebende Wirkung, da die Beziehung zwischen Tonika und Antitonika (RE-LA und DO-SO) nicht die untere, sondern die obere Note stützt:
In meinen Analysen bezeichnet der Buchstabe omega die Ganztonleiter. Ich habe mit Absicht den Buchstaben gewählt, der am weitesten von alpha entfernt ist, da Bartók selbst sie als Gegensätze benutzte. Alpha ist im Charakter ”angespannt”, omega ist ”aufgelöst”. Diese Eigenschaft wird offensichtlich darin, daß die Ganztonleiter, im Gegensatz zu alpha- und pentatonischen Strukturen, nicht eine einzige reine Quart (noch auch eine reine Quint) enthält. Ohne sie wird jedoch der tonale Charakter des Akkords unstabil. Im Zwölfton-System kann man zwei omega-Skalen unterscheiden (6+6 Noten); sie stehen zu einander im Verhältnis ”geometrischer Dominanten” (c-d-e-fis-gis-ais und des-es-f-g-a-h): w1 and w2.
Kodálys Chorwerk Fancy schließt mit einer vollständigen omega-Harmonie, und stellt so das Glockengeläut dar: Bsp. 57
Dank ihres fließenden Charakters eignet sich die omega-Harmonie besonders gut zur Tonmalerei oder Landschaftsmalerei. Wir geben hier ein Beispiel von Kodály:
Die direkte Gegenüberstellung der alpha- und omega-Klänge ist wegen des Gegensatzes sehr wirkungsvoll. Im dritten Satz der Musik für Saiteninstrumente, Schlagzeug und Celesta verwendet das von einem hohen Becken begleitete zentrale ”Licht”-Thema diese Dualität. Das Motiv ist um die Note c zentriert. Je nachdem, ob es in Grundstellung oder Umkehrung auftritt, kann es mit omega-Akkorden (siehe Bsp. 56 oben) oder mit alpha-Akkorden begleitet sein.
Durch die periodische Wiederholung verminderter Dreiklänge entsteht eine geschlossene alpha-Struktur:
* In der Praxis verschmelzen die verschiedenen Fibonacci-Modelle – d.h. alpha- und Achsen-Harmonien, 1:2, 1:3, 1:5 Modelle und äquidistante Skalen – miteinander. Das Beispiel unten zitiert das Jagd-ostinato aus dem chromatischen ersten Satz von Bartóks Sonate für zwei Klaviere und Schlagzeug:
In den zwölf Noten des ostinato ist die gesamte chromatische Tonleiter enthalten. Zwischen den Anfangs- und Schlußnoten (Oberstimme a und es, Unterstimme fis und c) besteht eine Pol-Gegenpol-Beziehung; so wird die Achsen-Anordnung fis-a-c-es gebildet. Die Oberstimme ist aus der omega-Skala a-h-des-es-f-g gewonnen, deren Formel 2+2+2+2+2+2 ist; die Unterstimme dagegen aus der komplementären omega-Skala fis-gis-b-c-d-e. Die beiden Stimmen bewegen sich in parallelen kleinen Terzen (3). Motivisch ist jede Stimme aus kleinen Sexten (8) zusammengesetzt: die Oberstimme aus den übermäßigen Dreiklängen a-f-des und h-g-es und die Unterstimme aus den übermäßigen Dreiklängen fis-d-b und gis-e-c (8+8+8). Der harmonische Charakter des ostinato is durch gamma-Akkorde (3+5+3) und 1:3 Modelle definiert:
Die beiden 1:3 Modelle passen chromatisch ineinander.
Alle Strukturelemente sind also ”Fibonacci-Formeln”.
Die Grundform des diatonischen Systems ist die sogenannte akustische Skala: die DO-Leiter mit FI und TA. (Der Ausdruck ”akustische Skala” stammt von mir und wurde zuerst 1947 benutzt.) Auf c als Grundton ergibt sich: c – d – e– fis – g – a – b – c Die entsprechende akustische Harmonie besteht z.B. aus einem C-Dur-Dreiklang mit kleiner Sept b, akustischer Quart fis, und großer Sext a (”pastorale” Sext). Diese Harmonie wird akustische genannt, weil alle Noten ihren Ursprung in der natürlichen Obertonreihe haben:
Beispiele aus Bartóks Werken Bsp. 64
(Andere Beispiele finden sich später
unter Bsp. 90b und 109.)
Der akustische Charakter wird noch wirkungsvoller,
wenn er das Ergebnis einer Ausdehnung ist. Die Jagd-Fuge in Bartóks
Cantata
profana wird so explosiv, weil ihre kleine Terz sich zur großen
Terz verändert und schließlich zur akustischen Quart ausbricht
(MA-MI-FI):
Das Rahmenintervall der reinen Quint, das dieses Thema umschließt, und seine zwei ”Punkte” – die akustische Quart (FI) beim Halbschluß und der akustische MI-TA-Schritt am Schluß – verstärken nur die Natur-Atmosphäre der Szene. Der akustische Akkord enthält auch eine Ganztonleiter (omega), der nur ein Ton fehlt: b-c-d-e-fis. Daher kann der akustische Akkord leicht mit der omega-Skala gefärbt werden: Bsp. 66
Auch in Kodálys Musik ist die akustische Harmonik bekannt, obgleich er eine Vorliebe für den helleren lydischen Modus hatte: Bsp. 67
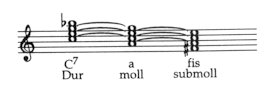
In Kodálys Musik besteht oft sehr wenig Unterschied zwischen der akustischen und der polaren Harmonik. So ist, zum Beispiel, der erste Akkord im oben zitierten Beispiel eine Kombination aus einem B-Dur-Septakkord und einem E-Dur-Septakkord. Der später unter Bsp. 87b gegebene akustische Akkord setzt sich aus den Gegenpolen C-Dur und Fis-Dur zusammen. Wir wollen nun versuchen, einen neuen Weg zu finden, um die akustische Harmonik abzuleiten. Dabei sollten wir von folgenden Beobachtungen ausgehen: die Paralleltonart zu C-Dur ist a-moll, und die zu a-moll ist fis-submoll (siehe S. 91):
Die Töne sind symmetrisch angeordnet – um das imaginäre Symmetrie-Zentrum RE (=d)! Wenn man die Töne der drei Akkorde kombiniert, erhält man eine akustische Harmonie. In beiden Fällen sind FI und TA charakterbestimmend. Und was wiederum offensichtlich ist: FI und TA sind exakte Spiegelungen von einander mit Bezug auf das Symmetrie-Zentrum RE. Die akustische Skala wurde zum statischen
”Farbakkord”, weil sie die beiden empfindsamen Noten, die den Dur-Charakter
bestimmen, vermissen läßt: anstelle von FA und TI (f und
h)
erscheinen FI und TA (fis und b). Was das Regenbogen-Farbspektrum
für die Optik ist, das ist die natürliche Obertonreihe für
die Musik.
Wenn Bartók oder Kodály die akustische Harmonie mit mehr ”Licht” ausstatten wollen, wird die kleine Sept des akustischen Akkords zur großen Sept erhöht. Bsp. 69
Wir werden diesen Akkordtyp – den Durakkord mit der großen Sept – als Hyper-Dur-Harmonie bezeichnen.
Das Hyper-Dur verkörpert den erhabensten Klangtyp in Bartóks und Kodálys Musik; so sind die Anfangsakkorde des Psalmus Hungaricus und des Te Deum Hyper-Dur-Harmonien. Dieser Akkord ist zum charakteristischen Begleitumstand der Apotheose geworden. Der Ursprung der bekannten ”Bartók-Signatur” geht auf das Hyper-Dur zurück: Bsp. 71
Das Hyper-Dur verdankt sein Licht nicht nur seinem Durcharakter und seiner großen Sept, sondern vor allem der Tatsache, daß es aus zwei reinen Quinten besteht (siehe Bsp. 70 oben). In den malerischsten Momenten verbindet sich die Hyper-Dur-Harmonie mit der akustischen Quart (FI): Bsp. 72
Das Hyper-Dur hat ein Gegenstück im Hyper-Moll. Dieser Akkord baut sich aus einem Molldreiklang mit großer Sept auf. Der übermäßige Dreiklang es-g-h trägt dabei viel zur individuellen Farbgebung bei:
”Ihr Leitmotiv”, schrieb Bartók in einem Brief an Stefi Geyer. Dieser Akkord findet sich überall dort, wo der Text von Schmerz und Leidenschaft spricht (siehe Bsp. oben). Durch Umkehrung von Bartóks ”Liebes-Leitmotiv” entsteht ein merkwürdiger Akkord, der in Bartóks Werk mit dem Symbolgehalt des Todes assoziiert wird: ”Eros dreht seine Fackel nach unten!” Bsp. 74
Diese Umkehrung des Hyper-Moll-Akkords erscheint, wann immer eine Sehnsucht erfüllt ist und, als Folge der Erfüllung, die Leidenschaft verebbt. In der Umkehrung wandert der übermäßige Dreiklang (es-g-h im vorangehenden Beispiel) in den unteren Teil des Akkords: a-f-cis: dies ist der Ursprung der neutralisierenden Wirkung. Der Schlußakkord in Herzog Blaubarts Burg ist ebenfalls eine Hyper-Moll-Umkehrung; die gesamte Oper endet also mit dem Symbol des Todes: Bsp. 75
Wenn es stimmt, daß das diatonische System lediglich ein Spiegelbild des chromatischen Systems***) ist, dann können diatonische Klangtypen erzeugt werden, indem die Schichten der alpha-Harmonien umgekehrt werden. Bsp. 76
Der diatonische Eindruck ist das unmittelbare Resultat der Tatsache, daß die alpha-Umkehrung von Quinten, großen Terzen und kleinen Septen (d.h. den nächsten Obertönen) bestimmt wird, die von den alpha-Harmonien selbst ausgeschlossen werden. Seltsamerweise legt die Harmonie mit einer Durterz über dem Grundton und einer Mollterz unter ihm den ”breitesten” Eindruck nahe. Bsp. 77
Und um die Querbeziehungen zu einem Ende zu bringen: die alpha-Umkehrung trägt in sich auch den Keim für die akustische Harmonie: Bsp. 78
Indem man die Noten c und fis vertauscht, kann eine polare Beziehung hergestellt werden (Sept- oder Nonakkorde auf C und Fis). Das Reprisen-Thema in Kodálys Háry-Vorspiel (siehe unten Bsp. 87b) kann als akustische Harmonie sowohl auf c wie auf fis aufgefaßt werden. Diese viertönige, polare Formel begann schon in der romantischen Musik an Boden zu gewinnen. So kann der tonale Kern der zehnten Kreuzwegstation in Liszt’s Via crucis, oder der fortissimo-Ausbruch, der in Verdis Otello das große Ensemble des dritten Aktes einleitet, folgendermaßen interpretiert werden: Bsp. 79
* Fassen wir hier die Grundtypen der beiden harmonischen
Systeme zusammen:
* Sich dem materialschaffenden Genius Bartóks und Kodálys zu nähern,
bedeutet, die der musikalischen Materie selbsttätig innewohnenden Gesetze besser zu erkennen.
*) Hierzu gehären auch Submoll-Akkorde verminderter Dreiklang mit kleiner Sept; siehe S. 91. (Hrsg.) ***) Siehe hierzu ausführlicher S. 56-58
|