

Next: Classification of Subgroups of
Up: A Symmetry Classification of
Previous: Introduction
Symmetries of Columns
We define a column by a real-valued function f on the cylinder
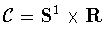 .
Let .
Let
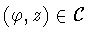 .
The function .
The function
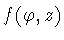 measures the height of the column in the direction normal to the cylinder
at the point
measures the height of the column in the direction normal to the cylinder
at the point
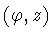 . .
The group of symmetries of the cylinder is
where 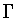 acts on
acts on
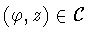 by
by
Multiplication in 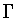 follows from the definition of the action.
Suppose that
follows from the definition of the action.
Suppose that
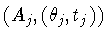 is in
is in 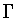 for j=1,2, where
for j=1,2, where
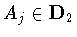 , ,
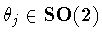 and
and
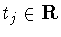 .
Then multiplication is given by .
Then multiplication is given by
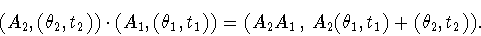 |
(1) |
We wish to classify columns by their symmetries. A symmetry of the
column
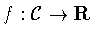 is
is
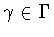 such that
such that
The symmetry group
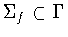 is the collection of all
symmetries of f. We classify
all subgroups
is the collection of all
symmetries of f. We classify
all subgroups 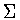 which are symmetry subgroups for some column f.
which are symmetry subgroups for some column f.
Our classification proceeds as follows. To each subgroup
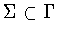 ,
we can associate the normal subgroup ,
we can associate the normal subgroup
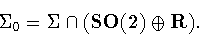 |
(2) |
(So 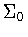 consists of the pure `translations' in
consists of the pure `translations' in 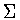 .)
Thus it suffices to .)
Thus it suffices to
- (i)
- classify the closed subgroups
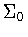 of
of
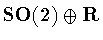 , ,
- (ii)
- for each subgroup
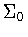 in (i), compute the subgroups
in (i), compute the subgroups
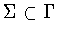 that satisfy (2.2).
that satisfy (2.2).
The calculation in (ii) is simplified by observing that 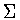 is
contained in the normalizer of
is
contained in the normalizer of 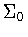 . .
As usual, we identify conjugate subgroups of 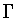 .
In addition, we identify subgroups that are related by axial scalings.
More precisely, we define the scaling transformation .
In addition, we identify subgroups that are related by axial scalings.
More precisely, we define the scaling transformation
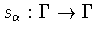 by
by
Provided
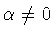 ,
this is an isomorphism. We say that two subgroups ,
this is an isomorphism. We say that two subgroups
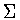 , ,
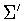 are related by a scaling if
are related by a scaling if
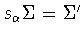 for some nonzero for some nonzero 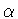 . .


Next: Classification of Subgroups of
Up: A Symmetry Classification of
Previous: Introduction
Marty Golubitsky
2001-01-29
|