

Next: Twisted Symmetry
Groups Up: Symmetries of
Columns Previous: Classification
of Subgroups of
Suppose that 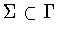 is a symmetry group. Then
is a symmetry group. Then
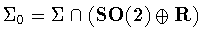 is one of the subgroups listed in Table
1. We say that
is one of the subgroups listed in Table
1. We say that 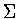 is an untwisted subgroup of
is an untwisted subgroup of 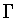 if
if 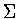 is conjugate to a subgroup of the form
is conjugate to a subgroup of the form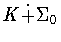 where K is contained in the subgroup H given in Table
1. The untwisted symmetry groups are listed in Table
2.
where K is contained in the subgroup H given in Table
1. The untwisted symmetry groups are listed in Table
2.
Table:The 22 untwisted symmetry groups
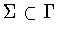
 |
It is not the case that every subgroup
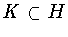 produces a symmetry group. For example, when
produces a symmetry group. For example, when
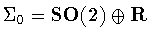 ,the only symmetry group
,the only symmetry group 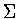 corresponding to
corresponding to 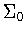 is
is 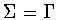 .(This isindependent of the restriction to untwisted symmetry groups.) To
verify this point, observe that
.(This isindependent of the restriction to untwisted symmetry groups.) To
verify this point, observe that
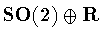 acts transitively on the cylinder
acts transitively on the cylinder 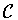 .Hence if
.Hence if 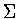 is the symmetry group of a function
is the symmetry group of a function
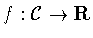 ,then f is the constant function.It follows that f is invariant
under
,then f is the constant function.It follows that f is invariant
under 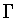 ,and that the symmetrysubgroup
,and that the symmetrysubgroup 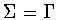 .
.
When 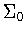 contains
contains 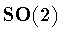 ,the function f isconstant on each horizontal cross-section of
,the function f isconstant on each horizontal cross-section of 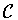 and hence automaticallyhas the symmetry
and hence automaticallyhas the symmetry 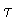 .In these cases, the only possibilities are
.In these cases, the only possibilities are
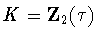 and
and 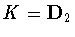 .Similarly, when
.Similarly, when 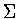 contains
contains 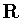 then automatically
then automatically 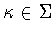 and the only possibilities are
and the only possibilities are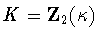 and
and 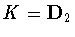 .
.
In all other cases, there are no restrictions on K other
than thecondition 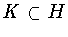 .
.


Next: Twisted Symmetry
Groups Up: Symmetries of
Columns Previous: Classification
of Subgroups of
Marty Golubitsky
2001-01-29
|
