

Next: Classification
of Columns Up: Symmetries
of Columns Previous: Untwisted
Symmetry Groups
We continue to suppose that 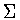 is a symmetry group with
is a symmetry group with
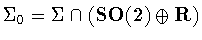 .We have
.We have  where H is given in Table 1
. The canonical projection
where H is given in Table 1
. The canonical projection 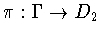 induces a projection
induces a projection 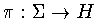 .
.
We say that a symmetry group
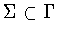 is twisted if it is not conjugate to an untwisted symmetry group.
Equivalently, there exists an
is twisted if it is not conjugate to an untwisted symmetry group.
Equivalently, there exists an 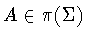 such that
such that 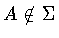 .
.
The next lemma states that, without loss of generality, we can always
supposethat the element 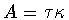 is not responsible for twisting.
is not responsible for twisting.
Lemma 2.5 Suppose that 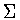
is a symmetry group and that 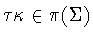
.Then there is a subgroup of 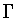
that is conjugate to 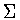
and contains 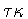
.The conjugacy leaves 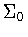
unchanged.
Proof: Recall that 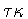 acts as -I on
acts as -I on 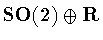 .By assumption
.By assumption 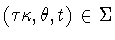 for some
for some .We conjugate by the element
.We conjugate by the element
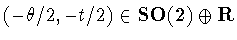 .Compute that
.Compute that
as required.
Proposition 2.6 Let 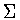
be a twisted symmetry group. Then either
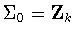
, 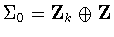
or 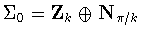
.In addition, 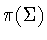
is one of the three subgroups 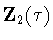
, 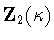
and 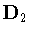
.
Remark: The possibility
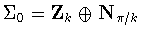 will be eliminated in the proof of Theorem
2.7.
will be eliminated in the proof of Theorem
2.7.
Proof: It follows from Lemma
2.5 that we can eliminate the subgroups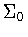 for which
for which 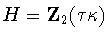 ,that is we can eliminate
,that is we can eliminate 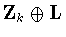 and
and 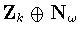 .
.
Next, suppose that 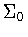 contains
contains 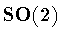 .As observed in theprevious subsection,
.As observed in theprevious subsection, 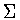 contains
contains 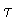 .If
.If 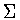 is larger than
is larger than 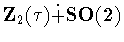 ,then
,then 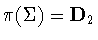 .It follows from Lemma 2.5 that
.It follows from Lemma 2.5 that
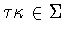 and hence
and hence 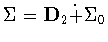 .In either case,
.In either case, 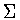 is untwisted. The possibility that
is untwisted. The possibility that 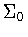 contains
contains 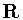 can be eliminated similarly. This completes the proof that
can be eliminated similarly. This completes the proof that 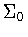 is one of the groups
is one of the groups 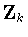 ,
,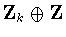 or
or 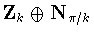 .
.
Recall that 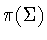 is a subgroup of
is a subgroup of 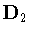 .If
.If 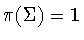 ,then
,then 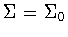 .If
.If 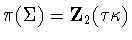 ,then
,then 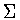 is conjugate to
is conjugate to 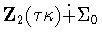 by Lemma 2.5. Hence, for
by Lemma 2.5. Hence, for 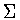 to be twisted,
to be twisted, 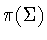 must be one of the three remaining subgroups of
must be one of the three remaining subgroups of 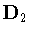 .
.
Theorem 2.7 Up to conjugacy
and scaling, there are seven twisted symmetry groups in 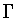
.These are as listed in Table 3
.
Table:The 7 twisted symmetry groups
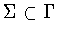 .
.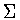 is generated by
is generated by 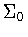 together with the generatorsof
together with the generatorsof 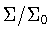 .Notation:
.Notation: 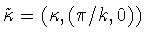 ,
,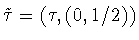
 |
Proof: By Proposition
2.6, we can assume that 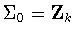 ,
,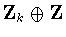 or
or 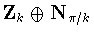 and that
and that 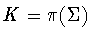 is one of the subgroups
is one of the subgroups 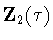 ,
,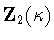 or
or 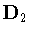 .We consider the three possibilities for K in turn.
.We consider the three possibilities for K in turn.
Suppose that 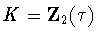 .Then
.Then 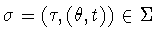 for some
for some  .Conjugating by
.Conjugating by
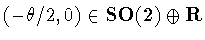 ,we can set
,we can set 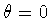 .Note that
.Note that
When 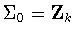 ,it follows that t=0 in which case
,it follows that t=0 in which case 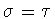 ,and there is no twisting. When
,and there is no twisting. When
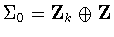 ,there is the additional possibility that
,there is the additional possibility that 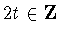 but
but 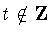 .Since
.Since 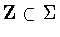 ,this reduces to the case t=1/2.The argument is more complicated when
,this reduces to the case t=1/2.The argument is more complicated when
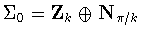 .Squaring yields the condition
.Squaring yields the condition
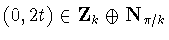 .Workingmodulo
.Workingmodulo 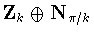 ,we can choose
,we can choose 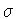 so that t=1. But still working modulo
so that t=1. But still working modulo
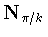 ,we can replace
,we can replace 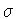 by
by 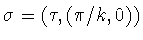 .Conjugating once again, we have
.Conjugating once again, we have 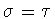 and there is no twisting.
and there is no twisting.
The case 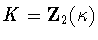 is similar. Conjugation reduces to
is similar. Conjugation reduces to
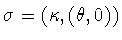 and squaring yields the condition
and squaring yields the condition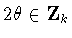 .Twisting occurs when
.Twisting occurs when 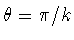 but onlyfor
but onlyfor 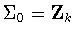 and
and 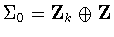 . Finally, suppose that
. Finally, suppose that 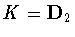 .We concentrate attention on the twogenerators
.We concentrate attention on the twogenerators
of 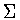 modulo
modulo 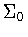 .Since the reflections are orthogonal, we can simultaneously conjugate so
that
.Since the reflections are orthogonal, we can simultaneously conjugate so
that 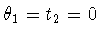 .Squaring the generators, we obtain that
.Squaring the generators, we obtain that
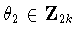 and either t1=0,
and either t1=0, 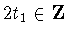 or
or 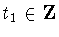 dependingon whether
dependingon whether 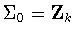 ,
,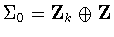 or
or 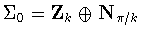 .The various combinations of generators yieldone untwisted subgroup and one
twisted subgroup for
.The various combinations of generators yieldone untwisted subgroup and one
twisted subgroup for 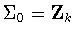 ,and one untwisted subgroup and three twisted subgroups for
,and one untwisted subgroup and three twisted subgroups for
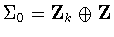 .Once again, there is no twisting when
.Once again, there is no twisting when
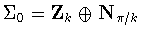 .The arguments are similar to the previous cases of K; we replace
.The arguments are similar to the previous cases of K; we replace
 by untwisted group elements.
by untwisted group elements.


Next: Classification
of Columns Up: Symmetries
of Columns Previous: Untwisted
Symmetry Groups
Marty Golubitsky
2001-01-29
|
