”Wir schaffen nach der Natur.” 
(Bartók)
 
 

DER GOLDENE SCHNITT
 
 

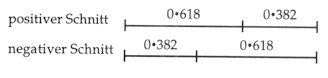
Praktisch bedeutet dies: wenn das Ganze als 1 angenommen wird, so ist das größere Segment mit etwa 0.618 anzusetzen und das kleinere mit etwa 0.382.

Bsp. 16

Unter strukturellem Aspekt betrachtet sind Bartóks größte Werke wahre Repräsentanten des Prinzips des goldenen Schnitts – oft vom Gesamt der Großform bis hinunter zum kleinsten Segment. So besteht z.B. der erste Satz der Sonate für zwei Klaviere und Schlagzeug aus 443 Takten. Multipliziert man 443 mit der Schlüsselzahl des goldenen Schnitts (d.h. mit 0.618), so erhält man 274 – und tatsächlich fällt in diesen Takt das Gravitätszentrum des Satzes: der Beginn der Reprise. 

Die Gesamtheit aller Sätze der Sonate für zwei Klaviere und Schlagzeug umfaßt 6432 Achtelwerte. Bezieht man den formalen Aufbau mit der Satzfolge

in die Überlegungen mit ein, so ergibt sich, daß der goldene Schnitt – nach 3975 Achtelwerten – genau auf den Beginn des zweiten, langsamen Satzes fällt. 

Der erste Satz in Bartóks Kontraste zählt 93 Takte. Sein goldener Schnitt – 93 mal   0.618 – markiert den Beginn der Reprise in der Mitte  von Takt 57. Der erste Satz des Divertimento enthält 563 Trioleneinheiten (aufgrund der wechselnden Taktangaben haben wir es hier nicht mit der Anzahl von Takten zu tun) und sein goldener Schnitt – 563 mal 0.618 – trifft ebenfalls auf dem Eintritt der Reprise (bei der 348. Trioleneinheit).

Bei oberflächlicher Betrachtung mag es unlogisch erscheinen, daß Wechsel im Tempo keinen Einfluß auf die Position der Schnittpunkte haben sollen. Der Widerspruch löst sich jedoch rasch auf, wenn wir uns klarmachen, daß der ”Herzschlag” der Musik ihr metrischer Puls ist, und nicht die absolute Dauer meßbarer Zeit, und daß diese metrischen Impulse weit energischer und emphatischer wirken als der Zeitabschnitt, in dem die Musik stattfindet. Subjektiv empfunden scheint Zeit mit schnellen Schlägen fiebrischer zu vergehen und sich mit langsamen mehr in die Länge zu ziehen.

Der goldene Schnitt kann sich auf zwei Weisen manifestieren: ”positiv” oder ”negativ”, je nachdem ob der größere Abschnitt dem kleineren vorangeht oder umgekehrt. Die Kombination aus lang + kurz stellt dabei die ”positive”, und die aus kurz + lang die ”negative” Konstellation dar:

Bsp. 17

Ein besonders gutes Beispiel für das Ausmaß, in dem Proportionen nach dem goldenen Schnitt musikalische Strukturen beherrschen können, findet sich in den sechzehn einleitenden Takten des ersten Satzes aus Bartóks Sonate für zwei Klaviere und Schlagzeug. (Um genauer zu sein: hier ist die Rede von Takt 2-17, da die organische Entwicklung des Werks tatsächlich von Takt 2 ihren Ausgang nimmt.)

Bsp. 18

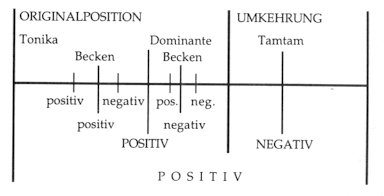
Hier ist eine Erläuterung dessen, was strukturell geschieht:
 

Durch die Unterteilung nach ”positiven” und ”negativen” Proportionen des goldenen Schnitts werden – ähnlich wie in der klassischen Epoche – musikalische Frage-Antwort Situationen geschaffen. Sowohl hinsichtlich der übergreifenden größeren als auch bezüglich der kleineren Bausteine erscheinen Fragen und Antworten, d.h. ”positive” und ”negative” Abschnitte, in symmetrischer Kombination, und zwar derart, daß sich die kleineren Abschnitte schließlich in einem ”positiven” Hauptabschnitt zusammenschließen. Das ist der Grund warum die Form – ähnlich einer dynamischen Schwellung – sich von pianissimo zu fortissimo hin entwickelt!
 

Es erübrigt sich anzumerken, daß der goldene Schnitt nicht als eine mathematische Regel auftritt. Es wäre sinnlos, in diesen Strukturen nach einer mathematischen Logik zu suchen.

Hier sollte auch hinzugefügt werden, daß es in Bartóks und Kodálys ”asymmetrisch-polyphoner” Kompositionstechnik nicht die Anzahl der Takte, sondern die der musikalischen Impulse ist, die die Proportionen bestimmt. Um ein typisches Beispiel zu geben: ganz am Schluß des Vierten Streichquartetts, beginnend von Takt 365, entsteht ganz klar der Eindruck, daß drei motivische ”Wellen” von fünf motivischen ”Wellen” (T. 365-374 und 375-385) beantwortet werden. Ebenso wird im Háry János-Vorspiel der vierfache Einsatz des Hauptthemas beantwortet mit sechs Themeneinsätzen – unabhängig vom Abstand der einzelnen Einsätze.

Hinsichtlich der Genauigkeit ist es entscheidend, sich klarzumachen, daß die Genauigkeit, die durch die Wahrnehmung kontrolliert wird, und jene Genauigkeit, die durch Rechnenarbeit nachgeprüft werden kann, zwei Seiten sind, die getrennt gehalten werden sollten. So habe ich selbst zum Beispiel den goldenen Schnitt intuitiv und empirisch entdeckt: meine Beobachtungen basierten auf tatsächlicher Erfahrung.

Wo endet Präzision und beginnt Ungenauigkeit? Als Beurteilungsgrundlage gebe ich folgende Erwägungen zu bedenken:
        (a) Die Abweichung zwischen den Systemen natürlicher Obertöne und temperierter Stimmung ist oft mehr als 1 % — und wird dennoch nicht entdeckt.
        (b) Das Vibrato sowohl einer Singstimme als auch eines Streichinstruments kann bis zu 2 % betragen — und wird doch im allgemeinen nicht als Ungenauigkeit betrachtet.
       (c) Da hinsichtlich des formalen Aufbaus in Bartóks Musik der goldene Schnitt die ”horizontale” Manifestation eines ”vertikalen” (harmonischen) Prinzips darstellt, sollte dieselbe Abweichung auch hinsichtlich der formalen Struktur erlaubt sein.

Der goldene Schnitt beruht auf drei Voraussetzungen:
       (a) Er erfüllt seinen Zweck nur, wenn er wahrnehmbar ist.
       (b) Er erscheint als ein organischer Bestandteil musikalischer Dramaturgie.
       (c) Er steht – als Symbol seiner ”organischen” Existenz – für eine Idee.

Das goldene Mittel ist nichts anderes als ein organisches Element der musikalischen Dramaturgie und bezieht seine Bedeutung nur aus der Beziehung zum Gehalt der Musik. Was uns dabei interessiert, ist vor allem der ”Effekt-Mechanismus” der Proportionen: die anziehende und abstoßende Kraft, die in den ”positiven” und ”negativen” Abschnitten zum Tragen kommt, und die Wechselbeziehung zwischen den Bausteinen.

”Zwei Elemente können ohne die Hilfe eines dritten nicht gut gepaart werden, da die beiden nur durch ein vermittelndes Glied miteinander in Verbindung treten; doch von allen Bindegliedern ist dasjenige das schönste, das sich selbst und die von ihm zusammengebrachten Elemente zu einem vollständigen Ganzen vereint.” (Plato: Timaeus)

Die statische Qualität und klassische Schönheit des Parthenon Athens kann zurückgeführt werden auf die Tatsache, daß in seiner Stirnseite – zwischen der Basis und dem Tympanon – genau zwei Quadrate Platz finden, andererseits kann seine dynamische Qualität – der Effekt des Schwebens, der das Gebäude wie von unsichtbarer Hand nach oben gezogen erscheinen läßt – eindeutig den Proportionen des goldenen Schnitts zugeschrieben werden. Wir reproduzieren hier der architektonische Strukturanalyse nach Zeising.

Bsp. 19

Vielleicht die schönste Verkörperung der Prinzipien des goldenen Schnitts im Bereich der Literatur findet sich in Dantes Göttlicher Komödie. Hier fällt der goldene Schnitt der insgesamt einhundert Canti auf das Ende des zweiundsechzigsten Canto. Dies aber ist genau der Punkt, wo Dante sich von Vergil trennt und seinen Weg mit Beatrice fortsetzt. Von hier an (d.h. beginnend mit Purgatorio XXVIII), ändern sich Sprachstil, Farbe, Ton und sogar Atmosphäre des Werkes.

Auch der große Physiker Einstein sprach sich für den goldenen Schnitt aus. Nach ihm ermöglicht der goldene Schnitt eine Proportion, die dem Schlechten Schwierigkeiten in den Weg stellt und zugleich die Entstehung des Guten fördert.
 
 

DIE  FIBONACCI–REIHE

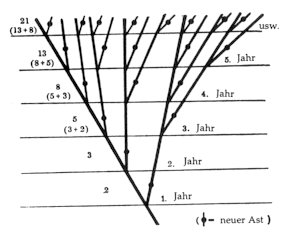
Die einfachste Sequenz der Verhältnisse des goldenen Schnitts, die sich in ganzen Zahlen ausdrücken lassen, ist als Fibonacci-Reihe bekannt geworden.

Man kann diese Reihe aus zwei Perspektiven lesen. Rückwärts betrachtet ist der goldene Schnitt von 89 gleich 55, der von 55 ist gleich 34, usw. Vorwärts gelesen ergibt sich, daß jede Zahl die Summe der beiden ihr vorangegangenen Zahlen darstellt (d.h. 2+3=5, 3+5=8, 5+8=13 usw.). Diese Reihe nähert sich tangential der Proportion des geometrischen goldenen Schnitts, d.h. der irrationalen Schlüsselzahl des geometrischen Mittels. Ein weiteres algebraisches Verhältnis ist das folgende: Das Quadrat jeder Zahl ist gleich dem Additionsprodukt aus der vorangegangenen mit der folgenden Zahl – mit dem Abweichungsgrad von plus/minus 1.

Die Fibonacci-Reihe ist die Verkörperung des Gesetzes natürlichen Wachstums. Wollen wir das durch ein Beispiel veranschaulichen. Wenn z.B. jeder Ast eines Baumes jährlich einen neuen Zweig hervorbringt, der junge Zweig jedoch seinen ersten Ableger jeweils erst nach zwei Jahren abspaltet, so entsteht als Abbild der jährlichen Progression die oben angegebene Zahlenreihe.

Bsp. 20

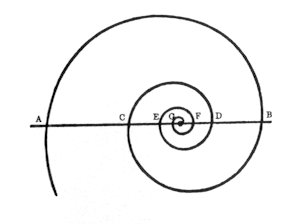
Wir haben einen schönen Representanten des goldenen Schnitts in der Natur: die logarithmische Spirale des Nautilus.

Bsp. 21

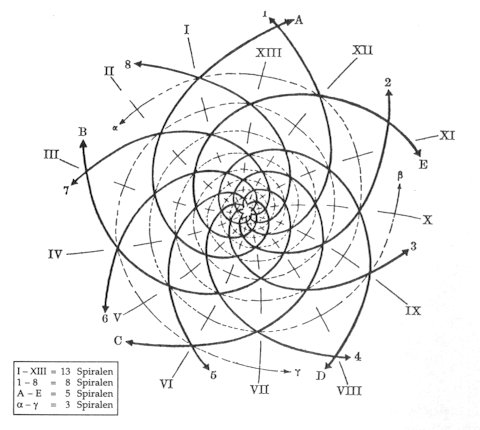
Wo immer wir eine gerade Linie durch das Zentrum der Spirale zeichnen, wird das Zentrum die Distanzen der Schnittpunkte (d.h. A—B, B—C, C—D, D—E, E—F, F—G) entweder in positiver oder in negativer Richtung – d.h. entweder nach rechts oder nach links – nach dem Proportionsverhältnis des goldenen Schnitts unterteilen. Die obige Figur stimmt erstaunlich mit Bsp. 18 überein!

Im Tannenzapfen, in dessen Zentrum (siehe die Abbildung) die Reihe ihren Ausgang nimmt, läuft ein System von Spiralen nach rechts und links, wobei die Anzahl der Spiralen stets in den Werten der Fibonacci-Reihe resultiert: 3, 5, 8 und 13 Spiralen.

Bsp. 22

Eine ähnliche Struktur findet sich in der Sonnenblume, der Ananas, der Kamille, sowie im Gänseblümchen, in der Margerite, im Kaktus, und nicht zuletzt auch in der Anordnung von Blättern am Zweig, in den Hörnern einiger Wiederkäuer – um nur die charakteristischsten Beispiele zu erwähnen.

Bartók übernahm diese Zahlenserie schon zu Beginn seiner Laufbahn, im Jahr 1911, als musikalisches Bauprinzip. Ein gutes Beispiel ist sein Allegro barbaro, dessen pochendes fis-moll ostinato in Gruppen von 3, 5, 8 oder 13 Takten unterteilt ist. Als vielleicht schönstes Beispiel einer musikalischen Darstellung der Fibonacci-Reihe gilt der erste Satz – die ”Pyramiden-Fuge” – der Musik für Saiteninstrumente, Schlagzeug und Celesta. (Eine ausführliche Analyse findet sich auf Seite 66-77.)
 

Und dies ist kein bloßer Zufall. Der elementarste musikalische Ausdruck des goldenen Schnitts ist das Prinzip der Pentatonik. Wenn ein Kind die einfachsten pentatonischen Phrasen singt, so tut es instinktiv nichts anderes, als ein Motiv nach den Proportionen des goldenen Schnitts, des geometrischen Mittels zu ”stimmen”. Das folgende Beispiel mag dies erläutern. Zählt man hier alle Intervalle in Halbtönen, so gleicht die Formel des LA–SO–MI-Motivs dem Verhältnis 2+3=5; fügt man nun noch das obere DO hinzu, so entsteht eine kleine Sext, d.h. ein Intervall von acht Halbtönen. Diese Sext aber zeigt ihrerseits eine Unterteilung in sowohl 5+3 als auch in 3+2+3.

Bsp. 23

Bartók erklärte einst: ”Volksmusik ist eine Naturerscheinung... Ihre Formen haben sich mit derselben organischen Freiheit entfaltet, wie es andere lebende Organismen tun: die Blumen, Tiere...”

Im ersten Satz der Sonate für zwei Klaviere und Schlagzeug steigt jeder neue Themeneinsatz eine Sprosse höher auf der Leiter der Fibonacci-Reihe:

Bsp. 24

Die harmonische Anlage der Exposition liefert einen Beweis für eine ähnliche Anordnung: jede neue Harmonie bewegt sich in der Skala des goldenen Schnitts einen Grad weiter voran.

Bsp. 25

Eines der Kennzeichen der Formen, die nach dem goldenen Schnitt aufgebaut sind, ist ihre geschlossene Qualität. Diese Formenwelt hat ein ganz besonderes Glühen, eine Lebensspannkraft und organische Geschlossenheit. Dies ist die unmittelbare Konsequenz der Tatsache, daß sich nach dem goldenen Schnitt gegliederte Strukturen nur in der lebendigen, organischen Natur finden lassen, in der anorganischen Natur, in der Welt der Kristallformationen, jedoch ganz fremd sind. (Siehe hierzu auch Beispiele 61 und 62.)