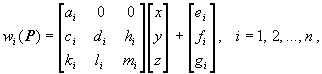Vector valued fractal interpolation functions  f : R ® R ²   can be introduced in the following setting ( see Barnsley  [1], [3], Barnsley et al. [2],  Massopust [13], [14]).

Given the set  of interpolating data  D = {P_i = [x_i  y_i  z_i]^T Î R³, x_i < x_i+1 , i = 0, 1,..., n}, one  builds n  affine transformations  w_i  : R³ ® R³  having the form
 

                                 (1)

where  P = [x  y  z]^T, and usually d_i , h_i , l_i , m_i  are real parameters while  a_i , c_i , k_i , e_i,  f_i  and  g_i are properly chosen constants depending on D. If  the coefficient matrix is denoted by  A_i and the translation vector by b_i, (1) takes the more compact  matrix form
 

The set  s(D) = {R ³; w₁, ..., w_n} is an affine Iterated Function System (IFS) associated to D. If all the affine mappings w_i are contractive, the IFS s(D) is hyperbolic and it has a unique attractor  F_DÌ R³.

This is the fixed point of the Hutchinson operator W( . ) = È_i w_i ( . ), a contractive operator on the complete metric space of  all non empty compact subsets of  R³ endowed with the Hausdorff  metric, H(R³, h). Thus, denoting by  W^m = W_° W ^m-1, and by  G an arbitrary compact subset of R³,  the attractor F_D satisfies

Any sequence of the type
 

is called  the  Hutchinson orbit of G , and  its elements are called preattractors (or prefractals ) of F_D.

Notice that, despite the uniqueness of the attractor of a hyperbolic IFS,  the multitude of  its preattractors offers a rich source of  of graphically interesting and sometimes  aesthetically very pleasent sets. Hutchinson orbits may  have various applications, ranging from computer graphics to number theory. Furthermore, the arbitrariness of the initial set G provides extra degrees of  freedom which prove useful for modeling purposes.

In the interpolation case, given D, the coefficients of  transformations w_i (i = 1,..., n) can be fixed so that  F_D  is  the graph of a continuous vector valued function  f : I ® R ² ( I = [x₀ , x_n] Ì R ) having the interpolation property, namely a function such that f(x_i) = [ y_i z_i]^T (i = 0,1,..., n). This function is called a generalized fractal interpolation function (Barnsley [2], [3]), or simply a vector valued  fractal interpolation function (Massopust [13], [14]) and its projections are called  hidden variable fractal interpolation functions. For more details see Section 2.  A nice application of  hidden variable functions is given  in Section 3.

A shortcoming of the fractal interpolants we deal with is lack of predictability of the shape of their graphs by means of the usual tools of CAGD.  The affine invariance of the IFS's whose attractors are graphs of  vector valued fractal interpolation functions is examined here, in Section 4. The  related results are illustrated by a graphical construction  based on visualization of a distance function between prefractal sets. Affine invariance property is one aspect of the problem of  predictability and modeling ability of IFS attractors, as dealt with in Kocic and Simoncelli [5]-[11].

Various examples of prefractal sets and applications are also illustrated here, in Section 5.