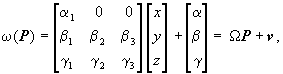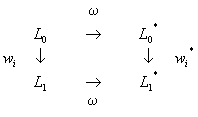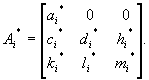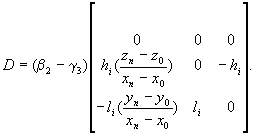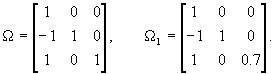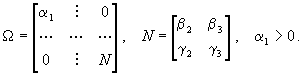|
4. Affine invariance As we mentioned before, by s(D,M)we denote both the IFS and the interpolation scheme (depending on M = {Mi, i = 1,.., n}) that associates to D Ì R3 the function f whose graph FD,M is the unique attractor of s(D,M). Definition 2. An interpolation scheme s(D,M) is invariant upon transformation w: R3® R3 iff for any DÌ R3, where FD,M denotes the attractor of the IFS s(D,M). Definition 3. An interpolation
scheme s(D,M)
is weakly invariant upon w
iff there exists a set of matrices M' = {Mi',
i = 1,.., n} such that, for any DÌ
R3,
Note that invariance upon w is weak invariance with M' =M. In this section we will examine the invariance of the interpolation
scheme introduced according to Theorem
1 with respect to affine mappings
w:
R3®
R3
having
the same structure as transformations
wi, more precisely
with a, a1, b, bi and g, gi real parameters, and a1 > 0. We will give conditions for the strict invariance of the general scheme, and will also discuss an interesting and very useful case of weak invariance. Let w transform the data set D into the set of points w(D) = D*= { Pi* = [xi* yi* z i*], i = 0, 1,..., n}. Notice that the special form of the matrix W introduced in (14) guarantees that w transform pairs of points having strictly increasing abscissas into pairs of points having the same property, therefore it is possible to build the IFS s(D*,M ) = {R3; w1*, ..., wn*} and consider the interpolation function corresponding to the transformed data set. At this point we need a general lemma, first. Also let (f° g)(x) = g(f(x)). Lemma 2. Given the IFS s(D) = {R3; w1, ..., wn} and a transformation w having equation (14), if wi° w = w° wi* (i = 1,..., n) , then w(FD) = Fw(D) . Proof. Let G denote the piecewise
linear interpolant of D. Then the
Hutchinson orbit of G is a sequence of polygonal lines converging
(in Hausdorff metric) to FD,
let this be {Lk = W k(G),
k
=
0, 1,...}. Also denote by L0* = w(L0)
the piecewise linear interpolant of D*
=
w(D),
and
let Lk* = W*(Lk-1*),
k
=
1, 2,... where W*( . ) = Èi
wi*(
. ). The sequence {Lk*} is the Hutchinson
orbit of w(L0)
and, therefore, Fw(D)
=
limk ®¥ Lk*
. If the diagram
commutes for all i, namely if wi° w = w° wi* , then at every new iteration k it holds Lk* = w(Lk), which means that Fw(D) = limk®¥ Lk* = limk ®¥ w(Lk) = w(FD) , being w a continuous function in R3. à Lemma 3 (Translation case). Let the affine mapping w be the translation w(P) = P + v, or, equivalently, let W = I in (14). Then the interpolation scheme is strictly invariant under w, namely (12) holds. Proof. According to (5)
wi (P) = Pi +Ai
(P
-Pn)
and, analogously
wi*(P) = Pi*+Ai
*(P
-Pn*),
with
Lemma 4 (Linear case). Let the affine mapping w have zero translation part, v = 0, so that it reduces to the linear transformation w(P) =WP. Let W have lower-triangular form with g2= 0. Then, (12) is valid if and only if b2 = g3. Proof. Under the assumptions of the Lemma, the difference di will have the value di = (w°wi*- wi° w)(P) = (Ai*W - WAi)(P -Pn), where Ai* is given by (16). For M=M', the matrix D = Ai*W - WAi has the following form
So, D is the zero matrix for all feasible M if and only if b2 = g3. Then, di= 0, the diagram (15) commute, and w(FD,M) = Fw(D),M. à The Lemmas 2, 3 and 4 can be combined into Theorem 3. Let the affine mapping w be defined by (14). Let the matrix W have lower-triangular form with g2= 0. Then, the interpolation scheme s(D,M)is strictly invariant under w, namely (12) holds if and only if b2 = g3. The next example uses a specific visual approach to illustrate Theorem 3. Example 3. Let D = {(0, 0, 0), (1/4, 0, 1/2), (1/2, 1/2, 1/2), (3/4, 1, 1/2), (1, 1, 0)}be the data, and let the choice d1= 0, d2= 1/4, d3= 1/4, d4= 0, h1= 0, h2= 0, h3= 0, h4= -1/4, l1= 1/4 , l2= 0, l3=l4=-1/4, m1= 0, m2= -1/4, m3= 1/4, m4= 0 be made. By this, the parameter matrix set M is fully determined as well as the hyperbolic IFS s(D) ={R3; w1, w2, w3, w4}with the attractor FD. Further, consider two different linear maps w(P) =WP and q(P) =W1P, where W and W1 are defined by
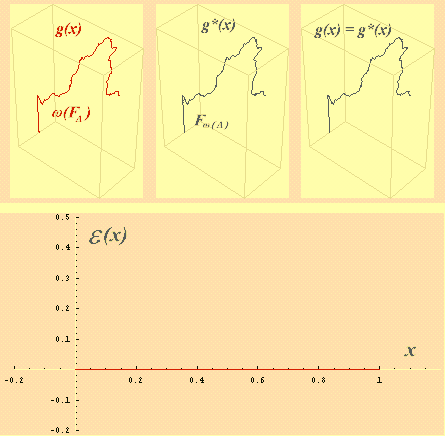
The Figure 4 (above) shows three diagrams. The leftmost one is the graph w(FD), the middle one is Fw(D) and the rightmost one represents both graphs simultaneously. Let the vector valued function g(x), 0 £ x £ 1, correspond to the graph w(FD) and let g*(x), 0 £ x £ 1, correspond to Fw(D). To compare two graphs better, the function e(x) = |g(x) -g*(x)|, 0 £ x £ 1, is calculated (Fig. 4, below).
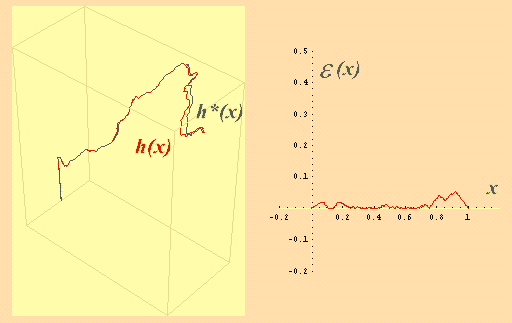
Figure 4. Affine invariance. Let q(FD) be the graph of the function h(x), 0 £ x £ 1, and let Fq(D) be the graph of h*(x), 0 £ x £ 1. The Figure 5 shows the similar comparison as above. This time the difference between the graphs q(FD) and Fq(D) (or h and h*) is visible (left). This is proved by the graph of e (x) = |h(x) - h*(x) |, 0 £ x £ 1, being different from zero.
Figure 5. Failure of affine invariance . The following theorem gives the conditions of weak invariance of an interpolating IFS. Theorem 4. Let s(D,M)be a hyperbolic block diagonal IFS. Let w be defined by (14) with W being a regular block diagonal matrix ( b1 = g1= 0 ).Then, the scheme s(D,M) is weakly invariant under w, namely (13) holds. Proof. Since s(D,M)
is a block diagonal, there exists a hyperbolic IFS t(Dyz,M)
so that s(D,M)
is its lifting (Definition 1), i.e.,
the 2D data set Dyz
= {Qi = [ yi zi]T
,
i
= 0, 1,..., n} obey conditions (11).
In the matrix form, these conditions are
where ri = [ fi gi]T . Since the scheme s(D,M) is invariant upon translation (Lemma 3), one can restrict transformation w given by (14) to the linear case w(P) = WP with W being a regular block diagonal matrix
Now, w(Pi) = [a1xi b2yi+ b3zi g2yi+ g3zi]T or, shortly w(Pi) = [a1xi (NQi)T ]T. Multiplying (17) with N from the left, and using I = N-1N (since W is regular, N is invertable) one gets NQi-1 = NMi N-1NQ0 + Nri, NQi = NMiN-1NQn+ Nri, which, by denoting takes the formEquations (19) are conditions (11) for the data set Dyz* with vi*(y, z) = Mi*[y z]T + ri*. Since Mi*and Mi are similar matrices, they share eigenvalues, so t(Dyz*,M') is also a hyperbolic IFS and M' = {Mi*, i = 1,.., n}. Let D* be a lifting of the data Dyz* on the mesh x0< x1< ...< xn and let s(D*,M') be the lifting of t(Dyz*,M'). By Theorem 2, s(D*,M') = {R3; w1*, ..., wn*} is also a hyperbolic block diagonal IFS. Let Mi* be the lower-right 2x2 block of the matrix Ai* that corresponds to the mapping wi*. Then, the first equality in (18) implies Ai*= WAiW-1 or Ai*W = WAi, for i = 1,..., n, i.e., by Lemma 2, w( FD,M) = Fw(D),M' . |