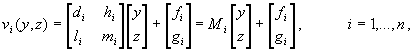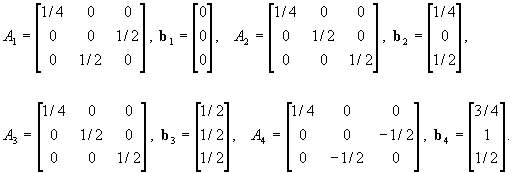Nevertheless, under feasible conditions, by carefully  choosing the IFS the parametric curve { f(t) = [f(t) y(t)]^T, t ÎI} can be built so to have the property of  self-affine planar interpolating curves, which is characteristic of most classical well known fractal curves such as the  Peano square (1890), the von Koch snowflake (1906) or the Sierpinski triangle (1915). Among these the Peano or space filling curves are especially interesting : these are curves  whose graph is identical to a nonempty pathwise connected compact subset of R ² (Barnsley [3], p. 240), and find interesting applications  in computer graphics, see for example  [15]. The construction is as follows.

Suppose that  the data set  from  the (y, z)-plane D_yz = {Q_i = [ y_i  z_i]^T, i = 0, 1,..., n} (n ³ 2) is given, satisfying
 

Given a polygonal line L with vertices {[p_j  q_j]^T, j = 0, 1, ..., m} (m ³ 2), such that [p₀  q₀]^T = [ y₀  z₀]^T = Q₀ and  [p_m q_m]^T = [ y_n  z_n]^T = Q_n , one can  build  a set of affine mappings { v_i : R ²® R ², i =  1,..., n}, having the form
 

                 (10)

and satisfying  the four interpolation conditions
 

Let  t(D_yz) = {R²; v₁,..., v_n} be the IFS connected to the transformations (10). It follows from (11) that for fixed  i , two out of six parameters d_i, h_i, l_i, m_i, f_i, g_i are free. For the reason of convenience, one may suppose that these free parameters are items of the matrix M_i. So, the set of matrices M = {M_i, i = 1,.., n} appears as the parameter of the IFS t(D_yz) and this fact will be stressed by the notation t(D_yz,M). If the elements of M_i for all  i = 1,.., n  satisfy conditions (7a) or (7b), it follows from the proof of Lemma 1 that r(M_i) < 1, and the IFS t(D_yz) is hyperbolic.

Definition 1. Given the mesh D_x = {x₀< x₁< ...< x_n } and the data set  D_yz = {Q_i = [ y_i  z_i]^T, i = 0,..,n}, we call  D = { [x_i  y_i  z_i]^T , i = 0, 1,..., n} a  lifting  of  D_yz on D_x. Let  t(D_yz,M)  be an  IFS built as above and let  D  be a  lifting  of  D_yz on D_x. Then, we call the IFS s(D) = s(D,M)  built according to Theorem 1, a lifting of t(D) = t(D_yz,M) on D_x.

The following theorem then holds.

Theorem 2. If the  IFS  t(D_yz,M) is hyperbolic, then its lifting s(D,M) is also  hyperbolic. Moreover, the attractor of t(D_yz,M) is the orthogonal projection of  the attractor of s(D,M) onto the (y, z)-plane. It has self-affine structure and interpolates the data set D_yz .

Proof.    For every  i = 1,..., n, (10) and (11) above  yield y_i - y_i-1- d_i(y_n -y₀) - h_i(z_n -z₀) = 0  and   z_i - z_i-1- l_i(y_n -y₀) - m_i(z_n -z₀) = 0 , which,  in connection with the hypothesis that s(D,M) is the lifting of  t(D_yz,M),  gives c_i= 0  and  k_i = 0  according to the formulas in Theorem 1.  Furthermore, under these hypotheses, the expressions for the known terms f_i and  g_i  from Theorem 1 are consistent with (11). This means that every transformation w_i splits  into two independent  components  w_i(P) = [u_i(x) v_i(y, z)]^T, the first one being  the contraction of  the real line u_i(x) = a_i x + e_i, and the second one, acting in the (y, z)-plane, being just v_i(y, z). Now, if the  IFS  t(D_yz,M) is hyperbolic,  r(M_i) < 1 holds for every i, and therefore  r(A_i) = max{|a_i|, r(M_i)}< 1 also holds for i = 1,..., n, and  s(D,M) is  hyperbolic, too.

Let F and F denote the attractors of s(D,M) and t(D_yz,M)  respectively.  Let  F_x and F_yz respectively denote projections of  F on x-axis and yz-plane. Let  F_i = w_i(F) and let  (F_i)_yz be the yz-projection of F_i . Then, by  the block diagonal structure of w_i it follows that w_i(F) = F_i = [u_i(F_x) v_i(F_yz)]^T or, v_i(F_yz) = (F_i)_yz . Also, È_iF_i  = F implies È_i(F_i)_yz = F_yz, which is equivalent to  È_i v_i(F_yz) = F_yz . So, F_yz  is the fixed point of the Hutchinson operator È_i v_i( . ) and the (unique) attractor of  t(D_yz,M). Accordingly, F = F_yz and F_yz  is a self-affine set.

It is straightforward to see, from  (11), that  D_yz Ì F_yz i.e., the attarctor of t(D_yz,M) interpolates the data set D_yz . à

As far as the matter of supplying two extra conditions to (11) that will define the remaining parameters of transformation v_i, according to the literature, there are two ways. The first one ([2]) uses n prescribed points in  the (y, z)-plane, {R_i, i = 1,..., n} and demands that v_i(p_j, q_j) =R_i, (j¹0,m), i = 1,..., n. In this way, the configuration of the points {R_i} influences the shape of the sequence of preattractors and the attractor itself.

The second method reduces the number of parameters of v_i to four by demanding that {v_i} belong to some subset of the set of affine planar mappings like in the case of  Peano or space filling curves [12].

Example 2 (Space-filling curve). Let D_yz = {(0, 0), (0, 1/2), (1/2, 1/2), (1, 1/2), (1, 0)}, and let L= {(0, 0), (0, 1/2), (1/2, 1), (1, 1/2), (1, 0)}. The mappings v₁, v₂, v₃  and v₄  determined by (11) and  by  v_1,4(1/2, 1)=(1/2, 1/4), v₂(1/2, 1)=(1/4, 1), v₃(1/2, 1)=(3/4, 1) define the hyperbolic IFS t(D_yz). Choice of the mesh {x_i}={0, 1/4, 1/2, 3/4, 1} leeds to the lifted IFS s(D) ={R³; w₁, w₂, w₃, w₄} where  the  matrix coefficients of w₁, w₂, w₃ and w₄  are

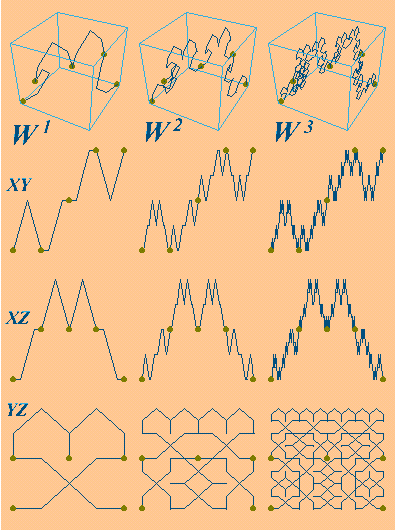
The first three iterations W ¹, W ² and W ³ of the Hutchinson operator W associated  with s(D), applied to L, are shown in Figure 3 (top) along with the corresponding projections on the coordinate planes. The yz-projections of W¹(L), W ²(L) and W ³(L) are successive approximations of  F_yz , the  yz-projection of the attractor F of s(D).  These self-affine continuous curves being contained in the unit square [0, 1]² suggest that F is also a continuous curve, it has self-affine structure and it  "fills" [0, 1]²  .