METHODS OF PERFECT COLORING

Abstract:  This paper presents two methods of coloring monochromatic plane and periodic mosaics by means of which color may be distributed making use of the symmetry group associated to the monochromatic mosaic and its subgroups. The main result is the Theorem where it is proved that, when the subgroup used for the two colorings is normal, the coloring result obtained is independent from the method used.

Keywords: Mosaic, Symmetry, Group, Tiling, Crystallographic Groups.

1  Introduction

All the plane periodic mosaics may be classified by means of the determination of their symmetry group, having 17 different classes as a result [1], although from an artistic point of view their number may be infinite. However, if we bear in mind the colors, the number of groups which determine the symmetry of the mosaic is greater [10]. These groups are called chromatic groups.

R.L.E. Schwarzenberger [8] contributed certain clarifications to the work of classifying chromatic compositions combining two monochromatic groups.

This paper presents two methods of coloring monochromatic plane and periodic mosaics by means of which color may be distributed making use of the symmetry group associated to the monochromatic mosaic and its subgroups. The main result is the Theorem where it is proved that, when the subgroup used for the two colorings is normal, the coloring result obtained is independent from the method used.
 
 

2  First Method of mosaic coloring

Let G be the crystallographic group associated to a periodic tiling T, and G₁ one of its crystallographic subgroups of index k. In these conditions, the union of basic, suitable, k tiles for G define a basic tile for G₁.
 

Method 1 (M1)

With k colors available, a basic tile for G₁ is colored by assigning a color to each of the k basic tiles of the tiling T (which has been primarily determined).

The coloration is then extended over the whole tiling by the action of group G₁ on the basic tile.

This form of coloring has the definition of the color stains, which we will deal with in a forthcoming article [3], and of the classes g_iG₁ and G₁g_i, with i = 1,2,¼,k, to the left and to the right respectively.

If G₁ is a normal subgroup in G, both classes coincide. In another case we will see that the colorings which can be obtained are less fine such as will be shown in the following example.

Example 1 Let G be the group of the type p4m associated to a pattern of squares which tiles the plane. Taking the translations T, and the reflection s_L from the G group represented in Figure 1, we form T È{s_L} and we take this as a set of generators of the subgroup G₁ which proves to be of the cm type. G₁ is not normal in G, as  if we take a rotation of G, for example, r_C,p/2, we have that:

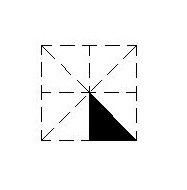
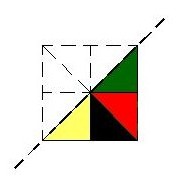
Figure 1: Basic tile for G.

Figure 2: 1st Basic tile for G₁.
 

Figure 3: Colored by the action of G₁ on the 1st basic tile.

Proposition 1 Let G₁ be a crystallographic subgroup of G of index k. Let K^G be a basic tile for G and K^G₁ a basic tile for G₁ obtained by uniting k tiles g_iK^G, i = 1,2,¼,k, with g_iÎ G and g_iG₁¹ g_jG₁ if g_i ¹ g_j. The resulting coloring when applying M1 to the tiling T_G = {gK^G; g Î G} from K^G₁ does not depend on K^G₁.

Proof:

Let K^G₁ and L^G₁ be two basic different G₁ tiles, obtained by uniting g_iK^G, i = 1,2,¼,k and g_iÎG, and [`g]<sub>s</sub>K<sup>G</sup>, s = 1,2,¼,k and  [`g]_sÎG, respectively.

For each g_iK^G a  g¹Î G exists such that g¹(g_iK^G) ÍL^G₁, therefore a unique [`g]<sub>s</sub> exists such that g<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>) = [`g]_sK^G. Later g¹g_i = [`g]<sub>s</sub> and g<sup>1</sup> = [`g]_sg^-1_i.

The permutation of colors which takes the color from g_iK^G in that of [`g]<sub>s</sub>K<sup>G</sup> permutes the T<sub>G</sub>   tile colors, colored by M1 starting from K<sup>G<sub>1</sub></sup>, in the colors obtained from L<sup>G<sub>1</sub></sup>. In fact, any tile obtained starting from g<sub>i</sub>K<sup>G</sup> by the action of G<sub>1</sub> will have the type h<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>). As h<sup>1</sup> Î G<sub>1</sub>, m = h<sup>1</sup>(g<sup>1</sup>)<sup>-1</sup> ÎG<sub>1</sub> and h<sup>1</sup> = mg<sup>1</sup>. Then, h<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>) = mg<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>) = m(g<sup>1</sup>g<sub>i</sub>K<sup>G</sup>) = m([`g]_sK^G). With the tiles g_iK^G and [`g]<sub>s</sub>K<sup>G</sup> having the same color as h<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>) and m([`g]_sK^G), the permutation which takes the color from g_iK^G to that of [`g]<sub>s</sub>K<sup>G</sup> also takes that of h<sup>1</sup>(g<sub>i</sub>K<sup>G</sup>) to that of m([`g]_sK^G).

Figure 4: 2nd basic tile. Coloring by G₁

If we change subgroup, logically, other results are obtained if the G₁ index is maintained in G like the basic G tile, see Figure 5 in which a subgroup of the p1m1 type has been used.

Definition 1 Let a periodic tiling be of R², in which each tile is colored with a color from among k possible colors. According to Senechal [9] we will say that k-coloring is perfect or compatible if each symmetry of the periodical mosaic discoloring induces a permutation of the k colors.

This type of coloring makes all the tiles which have the same color (for example, red) be transformed by means of a symmetry of the discolored periodical mosaic in tiles of the same color (for example, blue); symmetries of the discolored periodical mosaic do not exist which may mix colors in the meaning of transforming, for example, some red tiles in blue and others, also red, in green.

Proposition 2 The coloring done by M1 is perfect if and only if G₁ is normal in G.

Proof:

Let us call G_i the set of elements of G which stabilize the color i :

(Note: By means of g(i) = j we want to express that all basic tiles for G colored in the i color passes by means of the element g to another of the j color).

It is evident that G₁ ÍG_i. Let us see if the other inclusion is fulfilled.

Let K_i be an i colored tile. g₁ÎG₁ and K exist, and they are unique. Taking gÎG_i we have a K_i¢ tile, K_i¢ = gK_i = gg₁K, of i-color. Then gg₁ÎG₁ from where gÎG₁.

Now, let K_i be a basic i colored tile for G, K_i = g₁K. We will obtain another basic tile for G of j color applying any g of G to K_i : gK_i = gg₁K.

On the other hand, g₁¢ÎG₁ and K_j, will exist and they are unique, first basic tile for G of j color, such that:

Let K_i¢ be another basic tile for G of color i:

3  Second Method of mosaic coloring

Method 2 (M2)

The symmetries of G₁ act upon a chasen basic tile, for G, which is painted with a determined color (for example, yellow) and all its images because of the action of G₁ will have its the same color. Each one of the classes on the left hand side of G₁ in G will be identified with one of the available k colors and the symmetries of such a class are utilized to transform the original tile (in our example, black) into tiles which have the color assigned to such a class. In this way, the tiling remains painted with k colors.

Example 2 If M2 is applied to the basic tile for G of  Figure 1, and we take the same generators for G₁ - that is, s_L and T- the resulting coloring is the same that of  Figure 4.

Proposition 3 Let G be the symmetry group of a discolored periodical mosaic and G₁ one of its crystallographic subgroups of index k. Utilizing the M2 technique, the subgroup G₁ of G determines a perfect k-coloring so that G₁ is the stabilizer of one of the colors.

Proof:

We can see that the technique utilized guarantees that it is a perfect k-coloring. Let the K¢ and K¢¢ tiles be of the same color. g¢ and g¢¢ of G, exist, belonging to the same class, g¢G₁ = g¢¢G₁, and the basic tile for G, K, to color in such a way that:

Let g be any element of G:

later gK¢ and gK¢¢ has the same color (that corresponding to the gg¢G₁ class). As a consequence, g induces a permutation of colors.

Proposition 4 The correspondence which is established on coloring according to M2 between the elements of G and the group of permutations of k colors, S_k, is a homomorphism of groups.

Proof:

Taking left hand side classes a homomorphism can be defined between G and the group of the permutations of k elements S_k with the composition. In effect, representing the quotient G/G₁ by

The application  p: g Î G ® p(g), where p(g) Î S_k  is the matrix
 

is a homomorphism. In effect: 
 

In this homomorphism, used in the previous demonstration, we can verify that Ker p Í Ç_{i = 1}^k G_i = G¹, G_i being the stabilizer of i color, that is, fixed an i, G_i = {gÎG; gh_iG₁ = h_iG₁}.

Each one of the subgroups G_i is a class of conjugation of G₁.

Remark 1 A permutation of the K colors is associated to each element of G. That is, all symmetry operations have an element of the group of permutations of order k, S_k associated. Besides, as the product of symmetries is corresponded to the composition of permutations, we have seen that the nucleus of the homomorphism p: G ® S_k is formed by all the symmetries which leave all the colors invariant because it is associated to the permutation identity. The knowledge of G/Ker p is useful for being isomorphous to p(G), but it has the problem that knowing Ker p we know nothing about the permutation, p(g), which corresponds to any g. Therefore we have to substitute Ker p for a subgroup G₁, Ker p Í G₁, by means of which one unique color remains invariant. In the particular case in which G₁ = Ker p, it will be necessarily normal and the classes will coincide on the right and on the left.

Remark 2 In the demonstration of the Proposition 3 we have taken classes from the left. We make this obsevation because it is not the same to take classes from one side as from the other. Only in the case of G₁ being normal will the results coincide; this happens in the bi-color symmetry when k = 2.

Remark 3 One color is assigned to each class on the left, in this way the action of the elements of that class transform the assigned color to the G₁ class in it. Therefore, we can write G as finite union classes on the left, G = G₁Èh₁G₁ȼÈh_k-1G₁.

Remark 4 We believe we contribute a different method to obtain perfect k-colorings on those noted in Senechal [9] and before, giving an interpretation of their mathematical significance.

Corollary 1 If a tiling is colored by the action of a G group and one of its subgroups G₁ according to M2, the number of colors coincides with the index of G₁ in G.

4  Relationship between the two Methods

Proof:

It is deduced from above-mentioned results and that, in this case:

Definition 2 Let us call a chromatic group, with k colors, the trio (G,G₁,f ) where

• G, is a plane crystallographic group;
• G₁, a crystallographic subgroup of G of index k;
• f : G ® S_k the homomorphism given for f (g)(h_iG₁) = gh_iG₁.

Remark 6 The subgroup G¹ = Ç_gÎG gG₁g^-1, complete intersection of the conjugation family of G₁, is a normal and crystallographic subgroup of G. Besides, G¹ = Ker f.

Remark 7 The homomorphism f: G ® S_k induces a monomorphism:

References:

[1]

BOSSARD, Y., Rosaces, frises et pavages (Vols. 1,2), CEDIC, Paris, 1978.

[2]

PÉREZ-GÓMEZ, R., The four regular mosaics missing in The Alhambra, Comp. and Math. with Appls. 14, 2 (1987), 133-137.

[3]

PÉREZ-GÓMEZ, R. and RUIZ, C., Chromatic Plane Compositions, Visual Mathematics.

[4]

PÉREZ-GÓMEZ, R. and RUIZ, C., Tiling in Topological Spaces (to appear).

[5]

PÉREZ-GÓMEZ, R. and RUIZ, C., Kaleidoscopes in Topological Spaces (to appear).

[6]

PÉREZ-GÓMEZ, R. and RUIZ, C., Kaleidoscopes in the Alhambra, Proceeding of the IVth Workshop on Electromagnetically Induced Two-Hadron Emission(2000).

[7]

RUIZ, C. and PÉREZ-GÓMEZ, R., Visiones matemáticas de la Alhambra. El color, Epsilon 9 (1987), 51-59.

[8]

SCHWARZENBERGER, R.L.E., Colour Symmetry, Bull. London Math. Soc.16 (1984), 209-240.

[9]

SENECHAL, M., Colour Symmetry, Comp. and Math. with Appls. 16, 5-8 (1988), 545-553.

[10]

WIETING, T.W., The mathematical theory of chomatic plane ornaments, Marcel Dekker, New York, 1982.

[11]

VAN DER WAERDEN, B.L. and BURCKHARDT, J.J., Farbgruppen, Z. Kristallogr. 115 (1961), 231-234.

[12]

LUNGU, A.P. On coloring figures by different colors and their description in the framework of generalized color symmetry, (in Russian), Studies on general algebra, geometry and their applications, 104-110, 1986.

[13]

ZAMORZAEV, A.M., GALYARSKIJ, EH.I., PALISTRANT, A.F., Colour symmetry, its generalizations and applications (Tsvetnaya simmetriya, ee obobshcheniya i prilozheniya), (in Russian), Shtiintsa, Kishinev, 1978.

[14]

ZAMORZAEV, A.M., KARPOVA, Yu.S., LUNGU, A.P., PALISTRANT, A.F., P-symmetry and its further development (P-simmetriya i ee dal'nejshee razvitie), (in Russian), Shtiintsa, Kishinev, 1986.

Ceferino Ruiz
Dpt. Geometrí a y Topologí a,
Univ. Granada,
18071- Granada, Spain.
e-mail: ruiz@ugr.es