CHROMATIC PLANE COMPOSITIONSR. Pérez-Gómez 1andCeferino Ruiz 2
Keywords: Mosaic, Symmetry, Group, Tiling,
Crystallographic Groups.
1 IntroductionWe study the general problem of coloring a periodical plane mosaic, carried out by the action of a crystallographic group. Several authors (see [10] and [11]) have studied this under the restrictive hypothesis that all the colors appear equally proportionate on the chromatic composition and, even, that the crystallographic group used permutes, transitively, the color stains (perfect colorings).
The article is illustrated with multiple examples,
extracted fundamentally from the Alhambra of Granada (Spain), where we
point out the last example which shows how the isotropy of the color subgroups
may be neither normal nor comparable amongst themselves. However, the chromatic
global isotropy always is normal, for being the complete intersection of
a family of conjugated subgroups.
2 Color StainsTaking the term color in a wide sense which includes, apart from its own meaning, any characteristic of a tile, each tiling may be colored which allows us to represent a new dimension on the plane. In a precise way we establish:
Everything said about chromatic plane k-color compositions is extended, in a natural way, to mosaics, obtaining mosaics of color. That is, when a chromatic plane composition has a associated tiling T whose support is all the plane S(T) = R2 which will be called a mosaic of color. As a paintbrush colors tiles, we can associate the color of the tile to its points. This correspondence between points and colors is not one-to-one for which, in general, we do not have an application between the support, S(T), and the set of colors, but a multiform application. Proposition 1 In a chromatic composition points of the tiling which are colored with more than one color may exist. Proof: If two tiles are cut on the edge, the paintbrush will give these points the colors corresponding to such tiles, more than one of them being able to correspond to one point . In fact the points with more than one color, that neccesarily are in basic design, B( T), belong to the cement or plaster which join the pieces of tiles, or mark the essential pattern of the stucco or plasterwork. Definition 2 Let us call grey points of
the mosaic of color, or of the plane chromatic composition those points
of the tiling which are colored with more than one color. The grey points
form part of the basic design of the tiling.
Figure 1: Grey points of the Polibone (tiling of The Alhambra). When the tiles of a tiling T have interior connexe, the following is verified. Proposition 2 If we consider an application m¢: S( T)-B( T) ®C, continuous and exhaustive, taking in C the discrete topology, a unique paintbrush exists m: T ®C, which assigns equal color to each point that m¢. Proof: As m¢ is continuous, it is constant on the connexed components of S( T)-B( T) and therefore, it is extended to a unique paintbrush m assigning the closure of each connexe component (tile of T) the constant color assigned by m¢ to the same. It still has to be determined how a chromatic plane composition can be enlarged mathematically to obtain a mosaic of color. To avoid problems of indetermination, we need the composition to be big enough for the rest of the mosaic to be obtained by translation . This is an abstraction which is necessary to speak with precision about the classification of the mosaics, such as those in the Alhambra. Definition 3 Given a plane chromatic composition (T,m,C), we will say that an isometry g of the plane is a symmetry of the chromatic plane composition if it verifies: Definition 4 The set of symmetries of the chromatic plane composition generates a subgroup of the group of isometries of the Euclid plane, that we will note Sim(T,m,C) and we will call it symmetry group associated to the chromatic plane composition, which in turn contains a normal subgroup formed by its translations, that we note T(T,m,C).
given that being S(T) = R2, g(S(T)) ÇS( T) = g(R2) ÇR2 = R2 for which S(g(T)ÇT) = R2 = S(T); having g(T) ÇT and T equal support and being the first set of tiles contained in the second, it results that g(T) ÇT = T, for which g(T) ÉT. Besides, S(g(T)) = S(T) = R2. On the other hand, as g is an isometry it results in that the g(T) tiles are only cut on their edge, for which g(T) cannot contain more tiles than T if there were a tile in g(T) that were not in T, it would cut some tile of T in its interior. Then g(T) = T. As a consequence of the before-mentioned, the condition 2) in Definition 3 is expressed as: 2') For each K tile of T, m(K) = m(g-1(K)). Therefore, the symmetries of a mosaic of color are plane isometries that, apart from transforming the mosaic in itself, keep the color. Definition 5 We will say a plane chromatic composition is periodic if T(T,m,C) is generated by two independent translations. Let us call M(T) the set of tiles È{t(T) / t ÎT(T,m,C)}. We announced [8] the following theorem
and now we present completely its demonstration.
Theorem 1 Let (T,m,C) be a chromatic, plane, and periodic composition. It is verified:
Proof: a) As the translations of T(T,m,C) are isometries, M(T) is a set of tiles. Let A1, A2ÎM(T) and pÎA1ÇA2, A1 and A2 are images by movements of tiles K1, K2 of T, translations which are obtained by successive compositions of symmetries of the chromatic plane composition (T,m,C).
being t Î T(T,m,C) and K Î T, is well-defined, then, by construction the elements of M(T) are of the form t(K). For that let us suppose that a tile of M(T) has two representations t1(K1) = t2(K2), K1, K2ÎT, t1, t2ÎT(T,m,C); we have that K1 = t-11(t2(K2)). t-11° t2 is the result of successively composing symmetries of (T,m,C) and inverse transformations of symmetries. The condition 2) of the Definition 3 guarantees that all keep the color, then m(K1) = m(K2). The uniqueness of m¢ is guaranteed by the construction and by the fact that m¢|T = m. c) In the demonstration of this paragraph we will make use of the observations made after the Definition 3. The symmetries of a mosaic of color, (T,m,C), are the isometries of the plane which verify g(T) = T and m(T) = m(g-1(T)). As both conditions are closed (stable for the inverse and composition) it results that, calling Iso(R2) the group of isometries of R2, then Sim(M(T),m¢,C) = {g Î Iso(R2) / g(M(T)) = M(T) and m¢(M(T)) = m¢(g-1(M(T)))}. Because of the construction of M(T) and of m¢ from (T,m,C), the symmetries of (T,m,C), generators of Sim(T,m,C), are in Sim(M(T),m¢,C), then Sim(T,m,C) ÍSim(M(T),m¢,C). By the same constructions, the elements g of Sim(M(T),m¢,C) which take the tiling T to g(T), with g(T) ÇT¹Æ are symmetries of (T,m,C), since that m¢|T = m, and these elements generate Sim(M(T),m¢,C), then the equality is proved. d) Lastly, this paragraph is an immediate consequence of c) and of the fact that M(T) is constructed from T by translations. In effect, T(M(T),m¢,C) = T(T,m¢,C). Then T(M(T),m¢,C) is a subgroup of movements with translations in two independent directions and discrete action. As the other symmetries have to be compatible with the movements [2] it results that the group Sim(C(T),m¢,C) is a plane crystallographic group. Let us observe that T is contained in M(T) and m¢|T = m. The mosaic of color (M(T),m¢,C) is the mathematical result of extending the chromatic plane periodic composition (T,m,C) to all the plane. Definition 6 Let (T,m,C)
be a plane chromatic composition or a mosaic of color for each cÎC,
we will call a color stain the set of the plane Mc
= S(m-1(c)). Each color
stain may identify itself by its own color.
Figure 2: Color stains of the Polibone.
Figure 2 bis: The Polibone in the Alhambra. Proposition 3 The color stains are coincident or they intersect on their borders. Proof: Direct consequence of the paintbrush being exhaustive, of the grey points being on the edge of the tiles and of the edge of the union of subsets is contained in the union of the respective edges. What relationship exists between the symmetry of the color mosaic and its stains? We begin from a crystallographic plane group G, and let us suppose that on acting on one of its basic tiles defines a T tiling, that can be colored by a paintbrush, m, in such a way that the action of each element g, of the group G, on the tiles of T produces a paintbrush, m°g, equivalent to m. This condition imposed on the paintbrush is equivalent to saying that the elements of G permute the color stains of T for which the compatibility results with that studied in the previous paragraph. The permutation of colors, sg, associated to an element g of G is given by the equation sg(m(K)) = m(g(K)). As the group G acts transitively on the tiles of T, it also results that it must be able to pass from one color stain to any other, which implies that all the colors intervene in the same proportion. The theories that we could qualify as complete only reach interesting mathematical results when, under successive hypotheses of regularity, they practically coincide with this version. Example 1 Beginning from a Bone is a basic tile
of a crystallographic plane group G, which could be of the p4
type, the basic design of the Polibone is obtained. The chromatic plane
composition of the Alhambra counts on four colors which we can take for
an application of this theory. In this way, the paintbrush, m,
takes values in C = {white, honey-colored, black, green}.
With the condition that G permutes these colors between themselves,
one of the resulting possible chromatic compositions is that of Figure
3. This is one of the five different ones, that is, not equivalent by permutation
of colors with which that group and number of colors may be constructed.
Figure 3: Polibone tetracolor. Would the Polibone of the Throne Hall of the Alhambra be obtained by this theory? For the reply to be affirmative, it would be necessary to have a set C of 8 colors, since the green stains or the honey-colored ones suppose, each one of them, an eigth part of the total. To obtain a coherent result between the theory and reality, we have to abstract and think that bones of the same real color have different theoretical color, or rather, 8 paint pots exist of which four are white, two black, one green and one honey-colored. When the elements of G permute all the colors of a mosaic of color in itself, calling Gc the set of elements of G that leave the color stain c, Mc, invariant, it results that each class of the G/Gc quotient coincides with the equivalence class of the elements of G which determine permutations on C such that they transform c into the same color. Therefore, the class number of the quotient, index of Gc in G, coincides with the number of colors of C, and therefore with the number of stains. These theories have the inconvenience in that they do not give an answer to many real situations, in those which some colors are predominant over others, such as we have seen in the previous example. Therefore, the problem of finding a mathematical theory
which interprets the periodic chromatic compositions without supposing
more jumps than those really necessary remains open. The following
method of coloring allows us to give a partial solution and the bringing
up-to-date of tables as that given in Wieting [11] or
in Santander et al. [9], in which the number of
possible color groups are shown according to the number of colors which
are used.
3 Method to obtain the chromatic plane periodic compositions.
|
|
(1) |
Example 2 Let G0 be a crystallographic plane group of the type p4g; G1,G2 and G3 subgroups of G0o f the type cmm, pmm and pgg respectively.
Let us form a succession G0 ÉG1É G2ÉG3 in which we express the index of each subgroup in the preceding group under each inclusion. Then:
|
|
from where, #(G0/G3) = 2×2×4 = 16
If we take a region unity with respect to Gi as a tile, it will be formed by a number of basic tiles with respect to G0 equal to #(G0/Gi). Therefore, a tile for G0 could decompose in different ways in tiles for the subgroups Gi since #(G0/Gn) admits the different indexes #(G0/Gi) as dividers? This fact allows us to group them in multiples of quantities of those indexes.
Let (TG,X,C) be a chromatic plane periodic composition. For each color c ÎC, we consider the color stain Xc tiled by means of X-1(c). Let Gc be the subgroup of isotropy of the color c formed by the transformations of G which leave the color c invariant. These elements are characterized by the equation X(gK) = M(K), for all K ÎX-1(c). It is verified that Sim(TG,X,C) ÍGcÍ G.
With the aim of being able to manage comfortably the family of subgroups {Gc / c ÎC}, we can suppose in what is left that all the subgroups are comparable, that is, that given the color c1 and c2 of C it is verified that Gc2 is a subgroup Gc1 or vice-versa. In the first case Gc2 ÍGc1, this fact means that each element of G which leaves the color c2 invariant also leaves the color c1 invariant.
When all the subgroups Gc are comparable, we can order the set of colurs C = {c1,c2,¼,cn} in such a way that Gci ÍGci-1, with i Î {2,¼,n}. Calling G0 = G ans Gi = Gci, it results in the chain of subgroups G0 ÊG1Ê ¼ÊGiʼ ÊGn.
Note that the elements of Gn must leave all the color invariant for which its elements are symmetries of color of the chromatic composition (TG,X,C); therefore, Gn = Sim(TG,X,C).
Because of the considerations made in the preceding
paragraphs we will suppose that all the subgroups Gi
are normal in G, being able to consider the chromatic finite composition
(TG/Gn = Gn\ TG,m,C)
with m°p = X.
Theorem 2 If the subgroups of isotropy of the colors of a chromatic plane and periodic composition (TG,X,C) are normal and comparable they verify:
- a) The number of tiles in Gn\ R2 colored with the color ci is equal to #(Gi/Gn).
- b) #(G0/Gn) = åi = 1n #(Gi/Gn)
- c) 1/#(G0/G1) +¼+ 1/#(G0/Gn) = 1
- d) (¼(((#(G0/G1)-1)¼)#(Gi-1/Gi)-1)¼#(Gn-1/Gn)-1) = 0
Proof: a) This is a consequence of G0/Gn acting transitive and effectively on TG/Gn, which has #(G0/Gn) tiles. As Gi/Gn transforms in itself the colored tiles of color ci, of these there has to be exactly #(Gi/Gn).
b) As all the tiles are colored, their number #(G0/Gn),
has to be the sum of the numbers of tiles in Gn\ R2
colored with different colors.
c) In Gn\ R2we obtain the tiling
TG/Gn
formed by #(G0/Gn) colored
tiles. For each color ci a stain is obtained
which occupies 1/#(G0/Gi) of the total
of TG/Gn. When i = 1,2,¼,n
results it is stated.
Also we may prove this result from 1 and b):
|
|
equalling:
|
and dividing by the first member, results:
|
and applying, again, c) the paragraph results.
d) We can transform the equation c) in this other which we will call the color equation:
|
(2) |
In effect, multiplying c) by #(G0/G1)¼#(Gn-1/Gn) and taking into account 1 have the result:
|
|
|
|
|
|
|
|
|
|
|
|
|
If we repeat the procedure:
|
|
|
|
The last step consists of:
|
|
Passing everything to the second member d) is followed.
The interpretation of the color equation is the following: In TG/Gn there is #(Gi/Gn) tiles of color ci, resulting from applying the group Gi/Gn on a tile which has not been previously painted with any of the colors c1,¼,ci-1. The procedure commences coloring with color c1 the tiles which there are of this color. The step from TG/Gn to TG is done by means of the procedure described at the beginning of this paragraph.
Example 3 Let us color by means of this procedure the polibone (Figure 4). Let G0 be a crystallographic plane group of the type p4g. Let us form the chain p4g É cmm ÉpmmÉ pgg.
In Example 2 we saw that #(p4g/pgg) = 16.
On the other hand,
|
We must extend the chain trivially:
|
|
Therefore the number of necessary colors is 6.
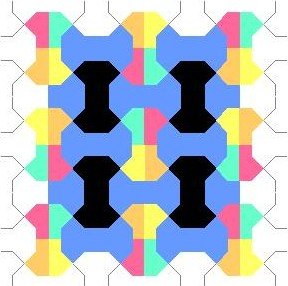
Figure 4
To conclude, we have colored in the following way: It is colored in the quotient of R2 by the action of Gn in such a way that once a unit region us colored for this group, the coloring is extended to all R2 by the action of Gn. In this tile, or in the quotient Gn\R2, one would work with the succesion of finite conmutative groups G0/GnÉG1/GnɼÉGn-1/GnÉ 1 in such a way that Gn\ R2 is descomposed in #(G0/Gn) tiles, of the action of G0/Gn on Gn\ R2, and it would be in this quotient where the groups Gi/Gn would work to color.
This version justifies the necessity of considering successions of normal subgroups, it is the only way of guaranteeing that the quotients of the groups are new groups that act in the quotient of the topological space. Besides, the problem of coloring is transformed into a finite problem of combinatory.
The way of acting which is followed in the chromatic plane and periodic compositions consists of looking at the succession of groups from the end, instead of doing so from the beginning. The last group leaves invariant all the tiling, including the colors, while the first leaves invariant only the discolored tiling.
This allows the general problem of coloring periodical mosaics to be reduced to that of coloring a unit region for Gn by means of a set of finite groups.
The before-mentioned theories are contemplated through that one developed previously. To suppose that the color stains are equisuperficial, the subgroups associated to two different stains are conjugated, for which they present equal index. The chains are reduced to G = G0ÉG1 = G2 = ¼ = Gn and on being
|
it has to be verified that
|
In this case it results that the number of colors used is #(G0/Gn) = #(G/Sim(TG,X,C)).
If we take two colors, the color equation tells us that the subgroups utilized must have index 2 in the group:
|
From the table of subgroups of the crystallographic plane groups [1] and if we take into account that the subgroup pmm must be counted twice, the number of dichochromatic plane groups is 46.
However, and it is the problem that we are presently
trying to resolve, there are situations in which the normality of the subgroup
is not needed and, however, we can apply the method of coloring together
with the color equation. Let us see how we can make the coloring of the
following color mosaic, from the basic design:

Figure 5: National Museum of Spanish-Moslem Art (Granada-Spain).
The symmetry group G associated to the basic design
is of the type cmm; we take the isometries {ta,sH,sL}
(see Figure 6) as generators of this group. A normal subgroup G0,
of index 2 and type pmm, is generated by {tv,th,sH,sL},
when tv = sLtasLta
and th = sLt-asLta.
A subgroup not normal, of type pmm also, is the subgroup
G1
generated by {tv,t3h,sH,sL}.
We form the chain of subgroups G ÉG0ÉG1.
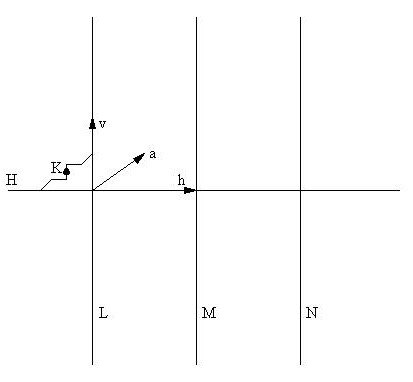
Figure 6
We colored in the following way [4]:
1st. We take the basic tile K for G, as in the above Figure 6.
2nd. We color the basic tile of color 1 (in reality it is black) for G and we extend this color by means of G1.
3rd. Again we color the basic tile thK of color 2 (green) and we extend this color with thG1 from K.
4th. We color of color 3 (honey-colored) and extend with t2hG1.
Note that the result is different if the class G1th and G1t2h are used in the 3rd and 4th steps.
Now, one half of the tiles are colored.
5th. We color again of color 0 (white) the tiles not colored above by means of subgroup G0, starting from any tile not colored (for example, taK).
In this way the mosaic of the figure is completely colored.
The subgroup of isotropy associated to the white color is G0.
The subgroups of isotropy associated to the other three colors: G1 to black, G2 to green and G3 to honey-color, are not normal subgroups of G and of G0; more exactly, G2 is generated by {tv,t3h,sH,sM}, and G3 is generated by {tv,t3h,sH,sN}. These three subgroups are not comparable between themselves. However, they are conjugated and their intersection is the normal subgroup G¢ of the global isotropy of all colors G¢, of type pm, generated by {tv,t3h,sH}:
The subgroups of isotropy associated to the other three colors: G1 to black, G2 to green and G3 to honey-color, are not normal subgroups of G and of G0; more exactly, G2 is generated by {tv,t3h,sH,sM}, and G3 is generated by {tv,t3h,sH,sN}. These three subgroups are not comparable between themselves. However, they are conjugated and their intersection is the normal subgroup G¢ of the global isotropy of all colors G¢, of type pm, generated by {tv,t3h,sH}:
References:
- [1]
- COXETER H.S.M., Coloured Symmetry. M.C. Escher. Art and Science, North-Holland (1986), 15-33.
- [2]
- HILBERT D. and COHN and VOSSEN S., Geometry and the imagination, Chelsea Publishing Company, New York (1952).
- [3]
- PÉREZ-GÓMEZ, R., The four regular mosaics missing in The Alhambra, Comp. and Math. with Appls. 14, 2 (1987), 133-137.
- [4]
- PEREZ-GOMEZ, R. and RUIZ, C., Methods of perfect coloring (Visual Mathematics).
- [5]
- PÉREZ-GÓMEZ, R. and RUIZ, C., Tiling in Topological Spaces (to appears).
- [6]
- PÉREZ-GÓMEZ, R. and RUIZ, C., Kaleidoscopes in Topological Spaces (to appears).
- [7]
- PÉREZ-GÓMEZ, R. and RUIZ, C., Kaleidoscopes in the Alhambra, Proceeding of the IVth Workshop on Electromagnetically Induced Two-Hadron Emission(2000).
- [8]
- RUIZ, C. and PÉREZ-GÓMEZ, R., Visiones matemáticas de la Alhambra. El color, Epsilon 9 (1987), 51-59.
- [9]
- SANTANDER M., RULL F. and GALLARDO F., Clasificación de grupos de color a partir de sistemas de generadores, Bol. Soc. Española de Mineralogí a 12 (1988), 59-66.
- [10]
- SCHWARZENBERGER, R.L.E., Colour Symmetry, Bull. London Math. Soc. 16 (1984), 209-240.
- [11]
- WIETING, T.W., The mathematical theory of chomatic plane ornaments, Marcel Dekker, New York (1982).
- [12]
- VAN DER WAERDEN, B.L. and BURCKHARDT, J.J., Farbgruppen, Z. Kristallogr. 115 (1961), 231-234.
- [13]
- LUNGU, A.P. On coloring figures by different colors and their description in the framework of generalized color symmetry, (in Russian), Studies on general algebra, geometry and their applications, 104-110, 1986.
- [14]
- ZAMORZAEV, A.M., GALYARSKIJ, EH.I., PALISTRANT, A.F., Colour symmetry, its generalizations and applications (Tsvetnaya simmetriya, ee obobshcheniya i prilozheniya), (in Russian), Shtiintsa, Kishinev, 1978.
- [15]
- ZAMORZAEV, A.M., KARPOVA, Yu.S., LUNGU, A.P., PALISTRANT, A.F., P-symmetry and its further development (P-simmetriya i ee dal'nejshee razvitie), (in Russian), Shtiintsa, Kishinev, 1986.
Rafael Pérez-Gómez
Dpt. Matemática Aplicada,
EU Arquitectura Técnica,
Univ. Granada,
18071 - Granada, Spain.
e-mail: rperez@ugr.es
Ceferino Ruiz
Dpt. Geometrí a y Topologí a,
Univ. Granada,
18071- Granada, Spain.
e-mail: ruiz@ugr.es
1991 Mathematical Subject Classification. Primary 20H15; Secondary 52C20.
1) Research partially supported by a Research Group in Applied Mathematics grant FQM-0191
2) Research partially supported by a DGICYT grant PB97-0785 and Research Group in Geometry grant FQM-0203



