Visual Magic Squares and Group Orbits I

John Pais (e-mail) and Richard Singer (e-mail)

“I am always doing that which I cannot do, in order that I may learn how to do it.” Pablo Picasso

Abstract

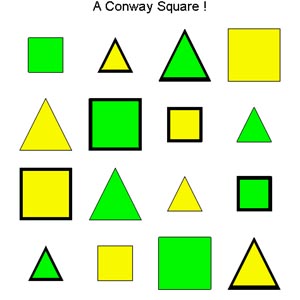
This paper is an essay in visual mathematics that strives to create a guided discovery in which the learner constructs his/her own math concepts, first intuitively, exploring, constructing, and counting 4´4 visual magic squares, and second analytically, using numerical representations and group orbits to classify and generate these visual magic squares. Euler and Conway visual magic squares are introduced and used to easily create and identify 528 of the 880 essentially different 4´4 magic squares. Euler items and their sets of complements are used to count Euler squares. Similarity classes of Conway items are introduced to create diagonal types and row types needed to classify, count, and generate Conway squares. In addition, by extending an intuitive math idea naturally constructed in this process, it is shown how Euler, Conway, and NonConway (4´4) magic squares can be generated using the orbits of appropriately chosen finite groups. In particular, it is shown that each of the six types of Conway squares introduced, can be generated by the transitive action of the Conway (square) group, B(4), i.e. the group of symmetries of the hypercube.

The intuitive-analytic duality of the learning experience is commonplace in doing mathematics (see, e.g. [4]). Thus, in order to develop this perspective, the reader is guided to the manifest realization that though a visual representation may be easier to use to see what is going on intuitively, an appropriate numerical representation often is necessary to provide an immediate, well-developed theoretical framework within which one can more easily state and verify important properties and results. Moreover, this paper is designed to be actively used for self study and math enrichment with an intended audience including both secondary school and college level students of mathematics. However, anyone interested in magic squares should enjoy and benefit from this new visual approach, presented in the first two sections, which provides the most intuitive and immediate way to create 4´4 magic squares that we know. Further, if the reader is familiar with finite groups, then our new approach using group orbits to generate all Conway squares should also be easily accessible. In addition, links to various MapleÔ worksheets are provided to aid in exploring and generating Conway squares. Indeed, the fact that we had a powerful computer algebra system available as a computational aid was crucial to engaging the daunting task of dealing with and exploring patterns and conjectures involving these 4´4 arrays of visual objects and numbers. So, we consider this work a paradigm example of the essential use of technology to productively extend ones limited computational ability in order to approach and solve a mathematical problem.