Visual Magic Squares and Group Orbits I

2. Conway Squares and Their Representations

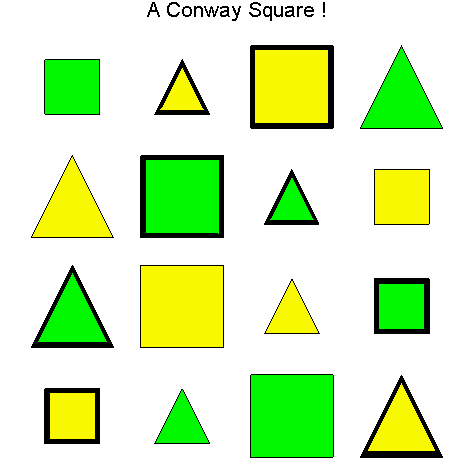
The colored shapes in the table below will be used to represent sixteen objects, with each one having four visual attributes: color, border, shape, and size. As indicated in the table, each attribute has two values: color can be green or yellow, border can be fat or thin, shape can be square or triangle, and size can be small or large.

Illustration 2.1

Definition 2.1. The collection of sixteen colored shapes in Illustration 2.1 will be called Conway items.  A set of four Conway items is said to have the Conway property just in case both values of each attribute (color, border, shape, and size) occur exactly twice. Notice that both the left and right main diagonals of the table in Illustration 2.1 each have the Conway property with green and yellow occurring twice for color, fat and thin occurring twice for border, square and triangle occurring twice for shape, and small and large occurring twice for size. However, none of the rows or columns have the Conway property.

A Conway square is any rearrangement of the table above in which each of the four rows, the four columns, and the two (left and right) main diagonals have the Conway property. In addition, we will refer to the process of creating Conway squares in pursuit of finding all Conway squares as the Conway game.

We note that our use of Conway items to create visual magic squares is our extension and modification of the visual approach used in Section 1 to create Euler squares. We call these new visual magic squares 'Conway squares' because in [1] (p. 778) John Conway calls a (base 10) 4 ´ 4 magic square perfect just in case nim-adding any number from 0 to 15 to every entry of it produces a magic square. Though only base 10 magic squares are considered there, this notion of preservation under nim-addition gave us a hint that considering a base 2 representation (see Definition 2.2 below) might be interesting and fruitful. Furthermore, in Section 3 of this paper we show how to use this base 2 representation to generate all Conway squares via finite group orbits.

Exercise 2.1. Play the Conway game by rearranging the Conway items in the table above until you have a Conway square. Here is a Conway items template that you can print out on photo quality paper and cut out to make your own pieces for the Conway game. Hint: Since both of the main diagonals in the table have the Conway property you can begin the game with both of these diagonals on the square.

Exercise 2.2. Play the Conway game starting with both diagonals as in Exercise 2.1, except that this time interchange the first two objects on the right main diagonal with the two objects below them on this diagonal. So, the new right main diagonal starting from the upper right and proceeding down and to the left should be: the large yellow square with thin border, the small yellow square with fat border, the large green triangle with thin border, and the small green triangle with fat border.

Definition 2.2. As with Euler squares, we also want to numerically code Conway squares. In order to do this, we will first numerically code our Conway items as ordered 4-tuples (vectors) of zeroes and ones. So, let [c, b, sh, s] be an ordered 4-tuple of zeroes and ones, then the different values of  c = 0, 1 will represent green, and yellow, respectively; the different values of  b =  0, 1 will represent fat and thin border, respectively; the different values of  sh =  0, 1 will represent square and triangle, respectively; the different values of  s =  0, 1 will represent small and large, respectively.  This is the base 2 representation of our Conway items. In order to convert it to a base 10 representation, we simply set n =  8c + 4b + 2sh + s.

The tables below illustrate this correspondence between Conway items and their numerical coding in base 2 and base 10.

Base 2 and Base 10 Coding of Conway Items

Illustration 2.2

If the Conway items in a Conway square are numerically coded using the base 2 (base 10) coding, then the resultant numerical square will be called a base 2 (base 10) Conway square. For example, consider the following Conway square and its two numerical codings.

Base 2 and Base 10 Coding of this Conway Square

Illustration 2.3

Exercise 2.3. Code each of the Conway squares found in Exercises 2.1 & 2.2 into their base 2 and base 10 representations, and then verify that these base 10 Conway squares are magic squares.

Theorem 2.3. Every base 10 Conway square is a magic square.

Exercise 2.4. Try to explain why Theorem 2.3 holds by finding numerical properties of the base 2 coding of a Conway square that force the corresponding base 10 coding to be a magic square.

Theorem 2.4. Let f be the natural mapping of Euler items onto Conway items given by mapping each Euler item in Illustration 1.1 onto the corresponding Conway item located in the same position in Illustration 2.1.
(1) If E is an Euler square, then f [E] (the square obtained by applying f to each item in E) is a Conway square. Furthermore, this mapping provides a 1-1 embedding of the set of Euler squares into the set of Conway squares.
(2) The embedding in (1) is not an onto mapping, i.e. every Euler square gets mapped to a Conway square, but some Conway square doesn't come from an Euler square.

Exercise 2.4.
(a) Using the mapping in Theorem 2.4 (1), map all of the Euler squares in Exercise 1.5 into Conway squares, and check (visually) that the resultant squares are Conway squares.
(b) After doing (a), try to explain why this mapping works by describing (for example) how a row of Euler items satisfying the Euler property must get mapped to a row of Conway items satisfying the Conway Property.
(c) In addition, verify Theorem 2.4 (2) by explaining why the Conway square in Illustration 2.3 could not have come from any Euler square using the mapping in Theorem 2.4 (1).
Hint for (b) and (c): It is easier to try to use the numerical representations of these squares, rather than directly using their visual representations in terms of Euler and Conway items. If you get stuck here, there is more helpful information below.

One interesting aspect of Theorem 2.4 is that we have been able to state it in terms of visual objects: Euler and Conway items, and in terms of visual magic squares: Euler and Conway squares. Though this visual approach is very appealing in that it allows us to easily create and recognize these visual magic squares, it is somewhat more difficult to use in actually proving results about these squares. Often that's the trade off one deals with in mathematics. Sometimes a visual representation is easier to use to see what's going on intuitively, but an appropriate numerical representation provides an immediate well-developed theoretical framework within which we can more easily state and verify important properties and results. Our intention in setting Exercise 2.4 was for the reader to experience this situation in doing math, and hence realize the necessity and usefulness of the numerical representations. The next theorem is essentially the numerical equivalent of Theorem 2.4.

Theorem 2.5. Let e be an Euler item, let [i, j] be its base 4 representation, and let [k, l, m, n] be the base 2 representation of [i, j]. Further, for each such e let g be the natural mapping sending [i, j] to [k, l, m, n].
(1) If E is the base 4 representation of an Euler square, then g[E] (the square obtained by applying g to each entry in E) is the base 2 representation of a Conway square. Furthermore, this mapping provides a 1-1 embedding of the set of base 4 Euler squares into the set of base 2 Conway squares.
(2) The embedding in (1) is not an onto mapping, i.e. every base 4 Euler square gets mapped to a base 2 Conway square, but some base 2 Conway square doesn't come from a base 4 Euler square.

Exercise 2.5. Explain why Theorem 2.5 holds. Again, note that Theorem 2.5 is just a restatement of Theorem 2.4 in terms of numerical representations of Euler and Conway squares, and so this exercise is really just a continuation of Exercise 2.4 (b) and (c) with a more detailed hint on what numerical representations to use.

Notation. In the following development we will use 'Euler square' and 'Conway square' to refer to both their corresponding visual item representations, and to their various numerical representations in different bases. With this notational convention we now see (can say) that it follows from Theorems 2.4 and 2.5 that every Euler square is a Conway square, but not vice versa. We noted in Remark 1.7 that it follows from Theorem 1.6 that there are 144 essentially different Euler squares. We know that the Conway squares include these Euler squares, and in the remainder of this section we will determine the total number of (essentially different) Conway squares. Following the hint in Exercise 1.7, we saw that it was not difficult to count Euler squares because of the strict and uniform constraints necessary to have an Euler square. In contrast, the fine structure of different types of Conway squares is more subtle, and we will now develop the necessary additional concepts we need to classify and count all Conway squares.  

Definition 2.6. Two Conway items are similar or in the same similarity class just in case they differ by an even number of attributes. If a and b are two similar items, we will write a ~ b, and denote the similarity class of a by [a], i.e. [a] = {b: b ~ a}. Further, any two Conway items that differ in all 4 attributes will be called complementary or complements of each other. If a and b are complementary items, we will write a' = b or b' = a, since complements are unique. In addition, any two Conway items that differ in exactly 2 attributes (hence agree in exactly 2 attributes) will be called bicomplementary or bicomplements of each other. Also, we will denote the set of all bicomplements of a by a* (note that bicomplements aren't unique).

In Illustration 2.4 below, we have labeled each Conway item with its base 10 coding in order to easily refer to each item.

Illustration 2.4

Using the numerical labels in Illustration 2.4, and considering the left main diagonal, we see that item 0 differs from itself in 0 attributes, item 0 differs from item 5 in 2 attributes (border and size), item 0 differs from item 10 in 2 attributes (color and shape), and item 0 differs from object 15 in all 4 attributes (color, border, shape, and size). So, the items on the left main diagonal, i.e. items 0, 5, 10, and 15, are all in the same similarity class.

Furthermore, items 0 and 15 are complementary, since they differ in all 4 attributes, and items 5 and 10 are complementary as well. In addition, items 0 and 5 are bicomplementary, and so are items 0 and 10, items 15 and 5, and items 15 and 10.

Exercise 2.6. Verify that the similarity relation ~ defined on Conway items is an equivalence relation, and that there are two equivalence classes w.r.t. ~ , each one of size eight. Further, verify that there are eight complementary pairs of items, that each similarity class contains four complementary pairs, and that each individual item has six bicomplements. Note that  you may represent these items using the base 10 labels in Illustration 2.4, e.g. 0 ~ 5 and 0' = 15.

Exercise 2.7. Verify that each similarity class can be written in terms of anyone of its elements as follows: [a] = {a, a'} È a*, i.e. the similarity class of a is comprised of a, the complement of a, and all the bicomplements of a.

Exercise 2.8. Write a clear, detailed, math argument explaining why complementary items have the same bicomplements, i.e. if a' = b, then a* = b*.

Next, we have the same Conway square as in Illustration 2.3, except that we have also labeled each object with its base 10 coding. Note that one similarity class {0, 5, 10, 15, 3, 6, 9, 12} occurs on the two main diagonals, and the other similarity class {14, 13, 2, 1, 11, 7, 8, 4} occurs in the middle of the top and bottom rows, and in the middle of the leftmost and rightmost columns of the table. Furthermore, in order to easily distinguish between these two similarity class, the Conway items in the second similarity class have their numerical labels underlined.

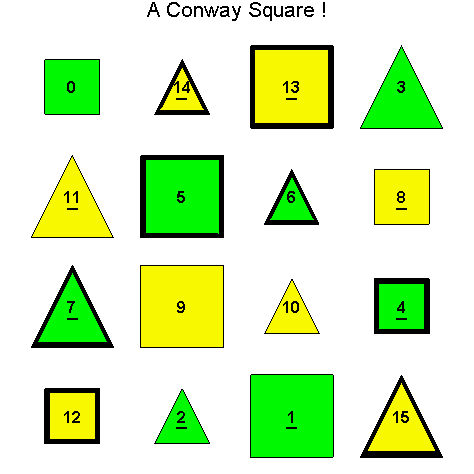
Illustration 2.5

Definition 2.7. (Diagonal Types) We will now define three different diagonal types of Conway squares that were previewed Exercises 1.2 in Section 1 and Exercise 2.3 in this section. For this definition we will let a, b, c, d, and complements a', b', c', d', range over the eight Conway items in one (unspecified) similarity class, and we will let w, x, y, z, and complements w', x', y', z',  range over the Conway items in the other similarity class.

1. A Type D1 Conway square is a Conway square with the items in the two similarity classes organized as follows:

Illustration 2.6

Note that for ease of viewing, we have partitioned the pattern for a Type D1 Conway square (the one on the left of the equality in Illustration 2.6) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'D1' corresponds to constructing a Conway square by placing a Conway item a in the upper left hand corner of the square and then placing its complement, a', one position below it on the left main diagonal. It turns out that beginning in this way and completing to a Conway square forces the resulting square to be of Type D1.

2. A Type D2 Conway square is a Conway square with the items in the two similarity classes organized as follows:

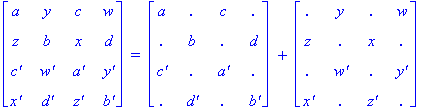
Illustration 2.7

Note that for ease of viewing, we have partitioned the pattern for a Type D2 Conway square (the one on the left of the equality in Illustration 2.7) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'D2' corresponds to constructing a Conway square by placing a Conway item a in the upper left hand corner of the square and then placing its complement, a', two positions below it on the left main diagonal. It turns out that beginning in this way and completing to a Conway square forces the resulting square to be of Type D2.

3. A Type D3 Conway square is a Conway square with all the objects of one similarity class occurring on the two main diagonals, with all the objects of the other similarity class occurring in the remaining positions, and with the following organization:

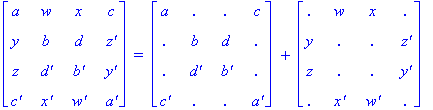
Illustration 2.8

Note that for ease of viewing, we have partitioned the pattern for a Type D3 Conway square (the one on the left of the equality in Illustration 2.8) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'D3' corresponds to constructing a Conway square by placing a Conway item a in the upper left hand corner of the square and then placing its complement, a', three positions below it on the left main diagonal. It turns out that beginning in this way and completing to a Conway Square forces the resulting square to be of Type D3.

Theorem 2.8. There are 384 Conway squares of each Diagonal Type (D1, D2, D3), yielding a total of 1152 Diagonal Type Conway squares.

Corollary 2.9. Each Diagonal Type Conway square is preserved under the eight symmetry transformations described in Remark 1.7, i.e. the symmetries of the (geometrical) square. Hence, there are 48 essentially different Conway squares of each Diagonal Type (D1, D2, D3), yielding a total of 144 essentially different Diagonal Type Conway squares.

Sketch of Proof of Theorem 2.8:  Type D1 Conway squares.
Note that we will use a Conway game construction to give a proof sketch, similar to the hint in Exercise 1.7 using the Euler game to count Euler squares. In this case, we will play the Conway game, building an arbitrary Type D1 Conway square, counting all our possible choices along the way, until the rest of the choices are forced. The reader is encouraged to play the Conway game while reading this proof sketch, mirroring all the steps in a specific case.

So, we begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the first position below a on the left main diagonal. Next, since we must have the same similarity class occupying the left main diagonal, we have 6 choices remaining for the first position below a' on this diagonal, say b, and then b' must go below it on this diagonal. Now, we have 4 choices remaining for the first position immediately to the right of a in the first row, say c, and then c' must go in the second row immediately below a. Thus, we have the following sequence of partial squares:

Finally, it can be seen by playing the Conway game that the rest of the entries are forced and in the correct positions for a Type D1 Conway square. Hence, there are (16)(6)(4) = 384 Type D1 Conway squares. ||

Sketch of Proof of Theorem 2.8:  Type D2 Conway squares.
We begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the second position below a on the left main diagonal. Next, since we must have the same similarity class occupying the left main diagonal, we have 6 choices remaining for the first position below a on this diagonal, say b, and then b' must go below a' in the last position on this diagonal. Now, we have 4 choices remaining for the second position to the right of a in the first row, say c, and then c' must go below a in the first position in third row. Thus, we have the following sequence of partial squares:

Finally, it can be seen by playing the Conway game that the rest of the entries are forced and in the correct positions for a Type D2 Conway square. Hence, there are (16)(6)(4) = 384 Type D2 Conway squares. ||

Sketch of Proof of Theorem 2.8:  Type D3 Conway squares.
We begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the third position below a on the left main diagonal. Next, since we must have the same similarity class occupying the left main diagonal, we have 6 choices remaining for the first position below a on this diagonal, say b, and then b' must go next below b on this diagonal. Now, we have 4 choices remaining for the last position to the right of a in the first row, say c, and then c' must go below a in the first position in fourth row. Thus, we have the following sequence of partial squares:

Finally, it can be seen by playing the Conway game that the rest of the entries are forced and in the correct positions for a Type D3 Conway square. Hence, there are (16)(6)(4) = 384 Type D3 Conway Squares. ||

Exercise 2.9. If you haven't done so already, play the Conway game while reading each proof sketch above, mirroring all the steps in a specific case for each of the three Diagonal Types. As a result, you will have constructed a Conway square of each of the three Diagonal Types. Try this yourself before viewing these examples: Type D1 Example, Type D2 Example, Type D3 Example

Exercise 2.10. By viewing Illustrations 2.6, 2.7, and 2.8, convince yourself that each of the eight symmetries of the square do indeed preserve each of the Diagonal Types. And so, as stated in Corollary 2.9, ignoring these symmetries there really are only 48 = 384/8 essentially different Conway squares of each of the three Diagonal Types.

Remark 2.10. Note that if we wished, we could enumerate all the Diagonal Type Conway squares simply by playing the Conway game as in the proof of Theorem 2.8, enumerating all of them by hand and verifying that each one is a Conway square. However, in Section 3 of this paper we will show how to do this in a more mathematical way, instead of using brute force.

Definition 2.11. (Row Types) We will now define three different row types of Conway squares that were previewed in Exercises 1.3 in Section 1 and Exercise 2.3 in this section. For this definition we will let a, b, c, d, and complements a', b', c', d', range over the eight Conway items in one (unspecified) similarity class, and we will let w, x, y, z, and complements w', x', y', z',  range over the Conway items in the other similarity class.

1. A Type R1 Conway square is a Conway square with all the items of one similarity class occurring together in the first two rows, all the items of the other similarity class occurring together in the last two rows, and organized in the following patterns:

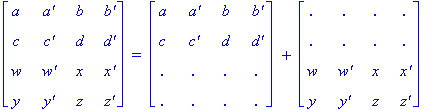
Illustration 2.9

Note that for ease of viewing, we have partitioned the pattern for a Type R1 Conway square (the one on the left of the equality in Illustration 2.9) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'R1' corresponds to constructing a Conway square by placing an item a in the upper left hand corner of the square and then placing its complement, a', one position to the right of it in the first row. It turns out that beginning in this way and completing to a Conway square forces the resulting square to be of Type R1.

2. A Type R2 Conway square is a Conway square with all the items of one similarity class occurring together in the first and third rows, all the objects of the other similarity class occurring together in the second and fourth rows, and organized as follows:

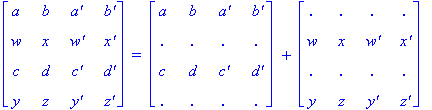
Illustration 2.10

Note that for ease of viewing, we have partitioned the pattern for a Type R2 Conway square (the one on the left of the equality in Illustration 2.10) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'R2' corresponds to constructing a Conway square by placing an item a in the upper left hand corner of the square and then placing its complement, a', two positions to the right of it in the first row. It turns out that beginning in this way and completing to a Conway square forces the resulting square to be of Type R2.

3. A Type R3 Conway square is a Conway square with all the items of one similarity class occurring together in the first and fourth rows, all the items of the other similarity class occurring together in the second and third rows, and organized in the following patterns:

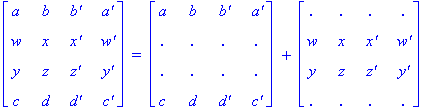
Illustration 2.11

Note that for ease of viewing, we have partitioned the pattern for a Type R3 Conway square (the one on the left of the equality in Illustration 2.11) into two partial squares, each depicting the location of one of the two similarity classes. We use a plus sign to indicate schematically how the two patterns are joined together.

Also, the name 'R3' corresponds to constructing a Conway square by placing an item a in the upper left hand corner of the square and then placing its complement, a', three positions to the right of it in the first row. It turns out that beginning in this way and completing to a Conway square forces the resulting square to be of Type R3.

Theorem 2.12. There are 384 Conway squares of each Row Type R1 and R2, and 768 Conway squares of Row Type R3, yielding a total of 1536 Row Type Conway squares.

Corollary 2.13. Each Row Type Conway square is preserved under the four symmetry transformations of the rectangle, i.e. a rotation by 180 or 360 degrees, or a reflection in the horizontal or vertical axis through the center. Hence, there are 96 essentially different Conway squares of each Row Type R1 and R2, and 192 essentially different Conway Squares of Row Type R3, yielding a total of 384 essentially different Row Type Conway Squares.

Sketch of Proof of Theorem 2.12:  Type R1 Conway squares.
Note that we will again use a Conway game construction to give a proof sketch as we did for Theorem 2.8.
So, we begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the first position to the right of a in the first row. Next, since we must have the same similarity class occupying the first two rows, we have 6 choices remaining for the next position in the first row, say b, and then b' must go to the right of b in the first row. Now, we have 4 choices remaining for the first position in the second row, say c, and then c' must go next to c in the second row. Thus, we have the following sequence of partial squares:

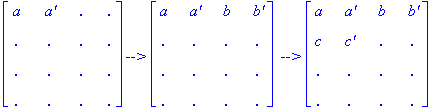
Finally, it can be seen by playing the Conway game that the rest of the entries are forced and in the correct positions for a Type R1 Conway square. Hence, there are (16)(6)(4) = 384 Type R1 Conway squares. ||

Sketch of Proof of Theorem 2.12:  Type R2 Conway squares.
We begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the second position to the right of a in the first row. Next, since we must have the same similarity class occupying the first two rows, we have 6 choices remaining for the position immediately to the right of a in the first row, say b, and then b' must go in the last position in the first row. Now, we have 4 choices remaining for the first position in the third row, say c, and then c' must go in the second position to the right of c in the third row. Thus, we have the following sequence of partial squares:

Finally, it can be seen by playing the Conway game that the rest of the entries are forced and in the correct positions for a Type R2 Conway square. Hence, there are (16)(6)(4) = 384 Type R2 Conway squares. ||

Sketch of Proof of Theorem 2.12:  Type R3 Conway squares.
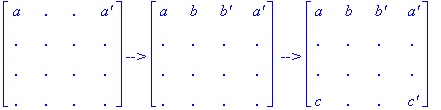
We begin by placing an arbitrary Conway item a in the upper left hand corner for which we have 16 possible choices, then a' must go in the third position to the right of a in the first row. Next, since we must have the same similarity class occupying the first two rows, we have 6 choices remaining for the position immediately to the right of a in the first row, say b, and then b' must go immediately to the right of b in the first row. Now, we have 4 choices remaining for the first position in the fourth row, say c, and then c' must go in the last position in the fourth row. Thus, we have the following sequence of partial squares:

In contrast to the other 5 types, it can be seen by playing the Conway game, that an R3 square is not yet forced and this is due to the fact that this is the only type in which the same similarity class (the other one, not yet filled in above) occupies the middle two rows of the square. Instead, it turns out that there are exactly two elements in this similarity class, say w and y, such that both of the following extensions of the game sequence above are possible, and from which each fourth partial square displayed is forced to an R3 Type Conway square.

Hence, there are (16)(6)(4)(2) = 768 Type R3 Conway squares. ||

Exercise 2.11. If you haven't done so already, play the Conway game while reading each part of the proof sketch of Theorem 2.12 above, mirroring all the steps in a specific case for each of the three Row Types. As a result, you will have constructed a Conway square of each of the three Row Types. Try this yourself before viewing these examples: Type R1 Example, Type R2 Example, Type R3 Example 1, Type R3 Example 2

Exercise 2.12. By viewing Illustrations 2.9, 2.10, and 2.11, convince yourself that each of the four symmetries of the rectangle do indeed preserve each of the Row Types. And so, as stated in Corollary 2.13, ignoring these symmetries there really are only 96 = 384/4 essentially different Conway squares of each type R1 and R2, and 192 = 768/4 essentially different Conway squares of type R3.

Remark 2.14. Note that if we wished, we could enumerate all the Row Type Conway squares simply by playing the Conway game as in the proof of Theorem 2.12, enumerating all of them by hand and verifying that each one is a Conway square. However, this would be quite tedious, so in Section 3 we will show how to do this in a more mathematical way, instead of using brute force.  In addition, we will show that the six types (D1, D2, D3, R1, R2, R3) introduced above exhaust the Conway squares, and hence there are exactly 528 = 144 + 384 essentially different Conway squares. Finally, we mention that in [Berlekamp, Conway, and Guy 1982] different types of magic squares are described. However, though we used those types as a starting point, we found them to be too coarse. Instead, we developed our Diagonal Types and Row Types based on similarity classes, in order to create more refined types needed for a more precise classification and easier counting.