|
Next: Acknowledgements: Up: Classification of Columns Previous: Discrete Corkscrew Columns Columns with Finite Symmetry -- Seven TypesThis types of column have neither a pure translation symmetry nor
any symmetry that includes a translation symmetry. There are seven possible
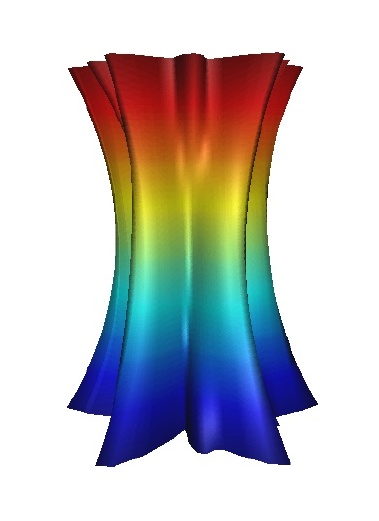
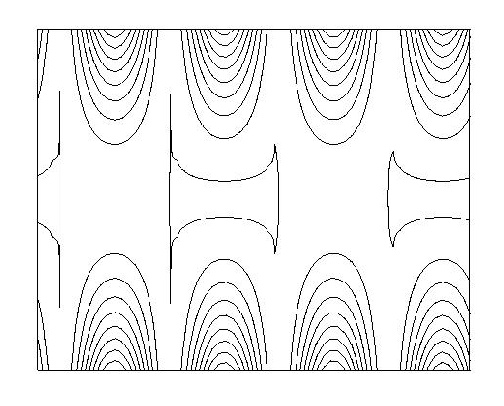
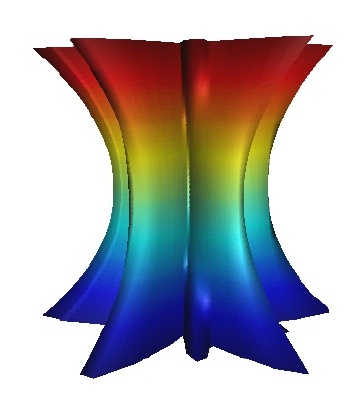
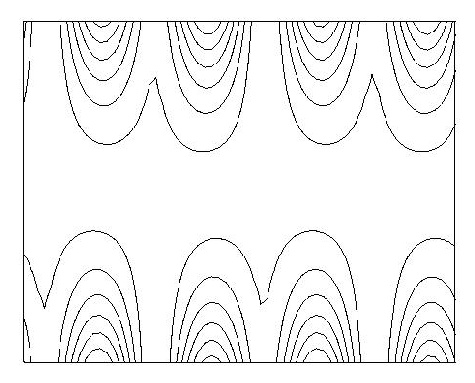
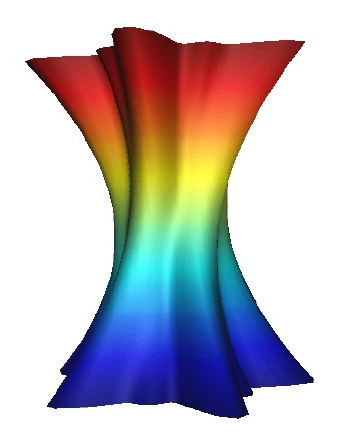
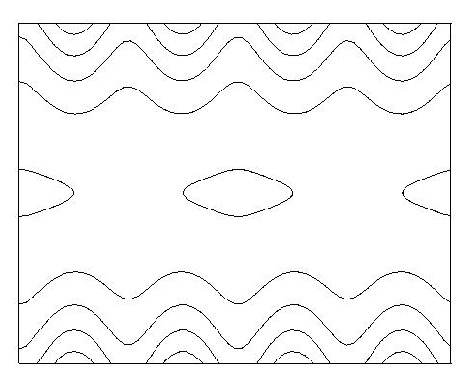
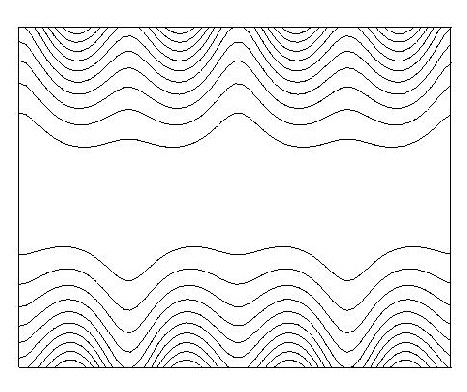
symmetry groups: An example of a column with no symmetry is given in Figure 23.Columns with just a single reflection or glide reflection are shown in Figure 24, 25, 26and 27, while columns with exactly two reflection or glide reflection symmetries are shown in Figure 28 and 29.
Next: Acknowledgements: Up: Classification of Columns Previous: Discrete Corkscrew Columns Marty Golubitsky 2001-01-29 |