Periodic Columns with No Corkscrew Symmetry -- Eight Types

Recall that 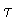$\tau$ is a reflection through a plane containing the axis of the cylinder and 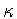$\kappa$ is the reflection through the midplane - the up-down symmetry. Each of these symmetries has a glide reflectionversion

$$\tilde{\tau} = (\tau,(0,1/2)) \qquad \tilde{\kappa} = (\kappa,(\pi,0)).$$

There are ten subsets 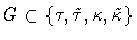$G\subset\{\tau,\tilde{\tau},\kappa,\tilde{\kappa}\}$ that form symmetry groups when coupled with 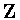${\bf Z}$ .These subsets are:

$$\{\kappa\} \quad \{\tau\} \quad \{\tilde{\kappa}\} \quad \{\t... ...{\tau},\tilde{\kappa}\} \quad \emptyset \quad \{\tau\kappa\}.$$

The symmetry groups of the corresponding periodic columns are: 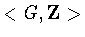$<G,{\bf Z}>$ --the group generated by G and 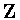${\bf Z}$ .Examples of columns having one purereflection symmetry are found in Figures  10and 11. Examples of columns having precisely one glide reflection are given inFigures  12 and 13. Columns having two reflections or glidereflections are shown in Figures  14,15, 16 and 17. The last two subsets correspond to symmetry groups that lie in infinite families and these infinite families have corkscrew symmetries (see Figures  21and 22).

   

Figure 10:Periodic column with up-down reflection.

   

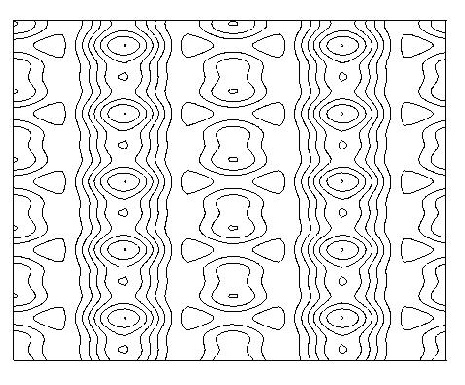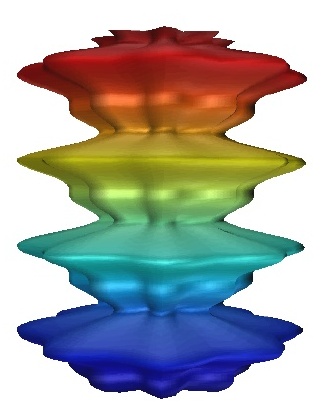
Figure 11:Periodic column with left-right reflection.

   

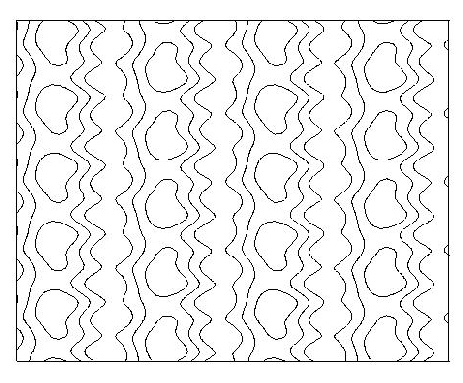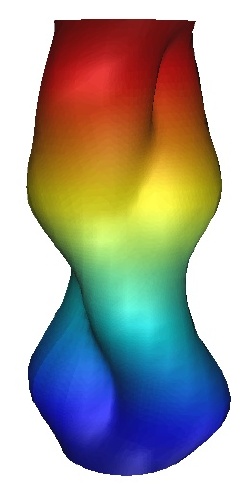
Figure 12:Periodic column with up-down glide reflection.

   

Figure 13:Periodic column with left-right glide reflection.

   

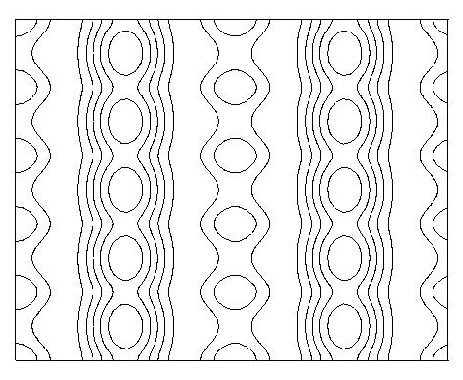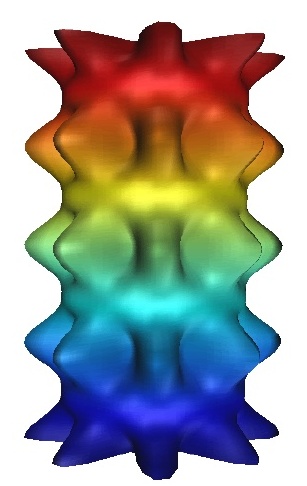
Figure 14:Periodic column with up-down and left-right reflections.

   

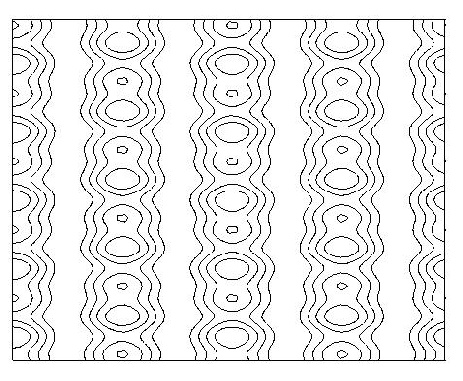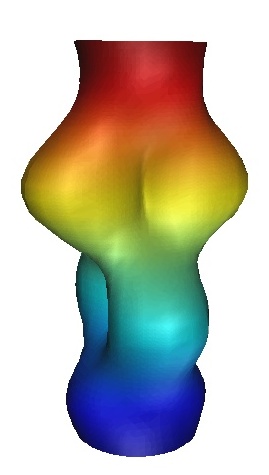
Figure 15:Periodic column with up-down glide reflection and left-right reflection.

   

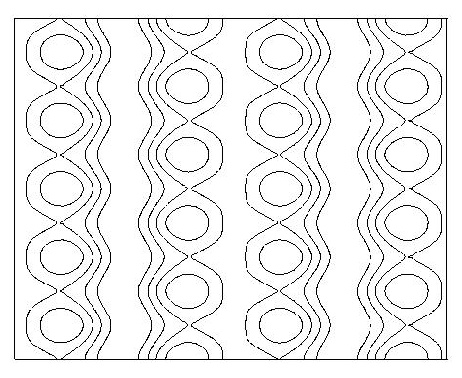
Figure 16:Periodic column with up-down reflection and left-right glide reflection.

   

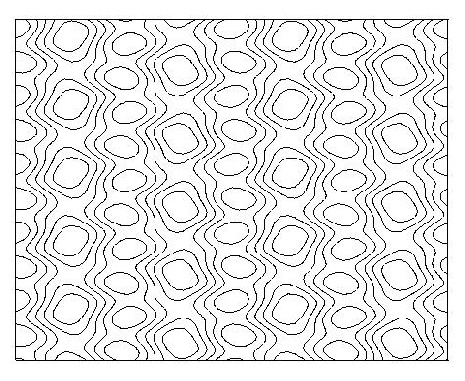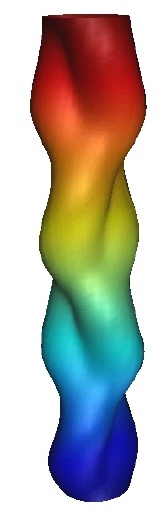
Figure 17:Periodic column with up-down and left-right glide reflections.