For the former longstanding four colour problem: "are the countries of each given map on the sphere colourable with 4 colours?" we have an affirmative answer since 1977 due to Appel and Haaken. In this article we look at the generalization of that problem to other surfaces, i.e. either a sphere with a finite number n of handles attached to it, or a sphere in which a finite number of circular holes have been filled with a Möbius strip each. Again we can ask: "what is the minimal number n of colours for such a surface such that any given map on the surface can be coloured with n colours?" We find the classical contributions to this topic in Gerhard Ringel’s book about the map colour theorem from 1974. It starts as follows: "In 1890 P.J.Heawood published a formula which he called the Map Colour Theorem. But he forgot to prove it. Therefore the world of mathematicians called it the Heawood Conjecture. In 1968 the formula was proven and therefore again called the Map Colour Theorem." This proof is due to Ringel and Youngs and co-workers. The problem is essentially that of finding for a given surface of genus g the smallest n for which the complete graph with n vertices can be embedded on that surface without self- intersections.

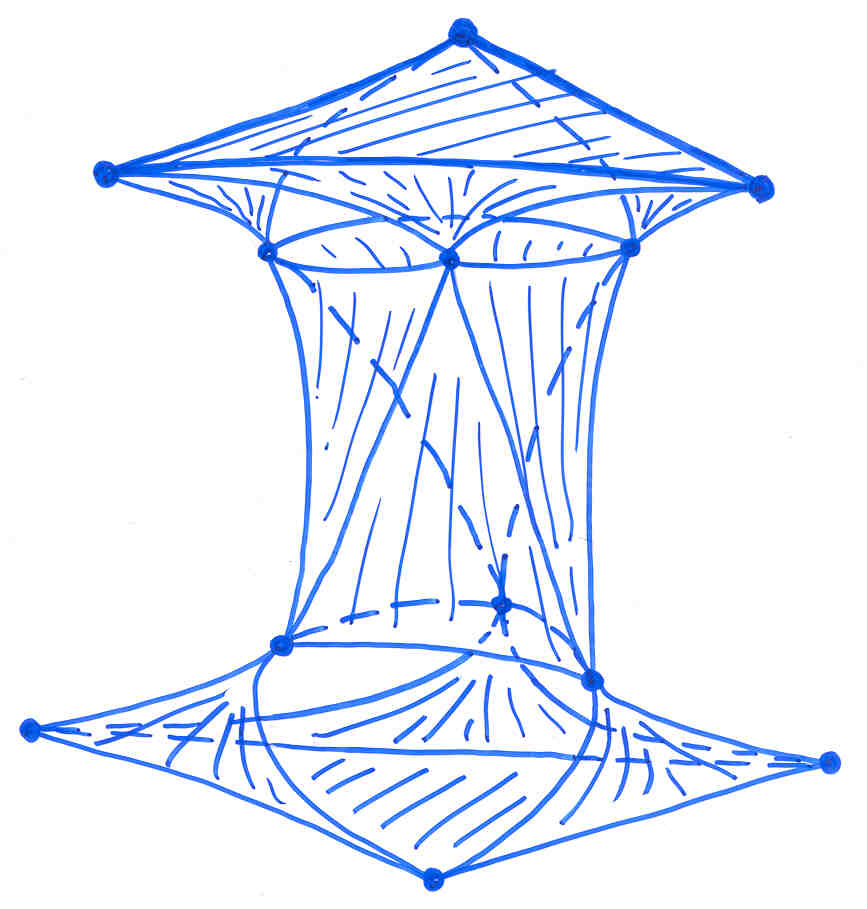
Ringel himself tried to find a model in the orientable genus 6 case in which the complete graph with 12 vertices can be embedded on the surface but he did not succeed. Try to start with the pottery model above and draw the 66 connecting curves on it without self-intersections.

The following model with a tetrahedral symmetry (corresponding to the proper rigid motions of the tetrahedron) shows such a solution in the highest symmetrical case. See also the website of Carlo Séquin for such a model.

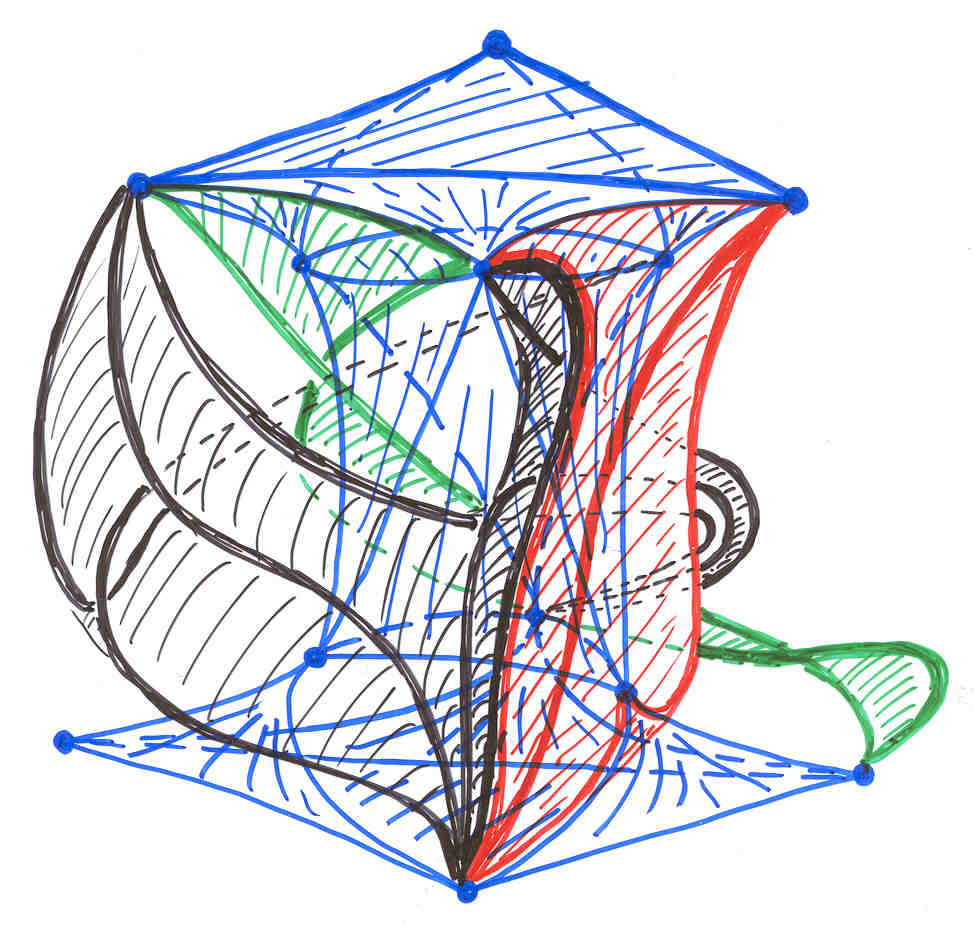
Whereas this solution is interesting in its own right, such a model has its interest in connection with a longstanding problem concerning the realization of triangulated 2-manifolds. Grünbaum has asked the following question: does every oriented triangulated 2-manifold (a sphere with g handles) have a polyhedral embedding in 3-dimensional Euclidean space without intersecting triangles? It has turned out that another combinatorial version of the complete graph with 12 vertices on an orientable surface of genus 6 plays an essential role as a counter example for that problem. The symmetry in that case is that of a planar regular triangle. The surface can be seen in the next figure. We have a rotational symmetry of order 3 and when putting the model upside down, we arrive at the same model again. Whereas the surface is easy to understand, a possible shape for the complete graph with 12 vertices on that surface is more difficult to find.

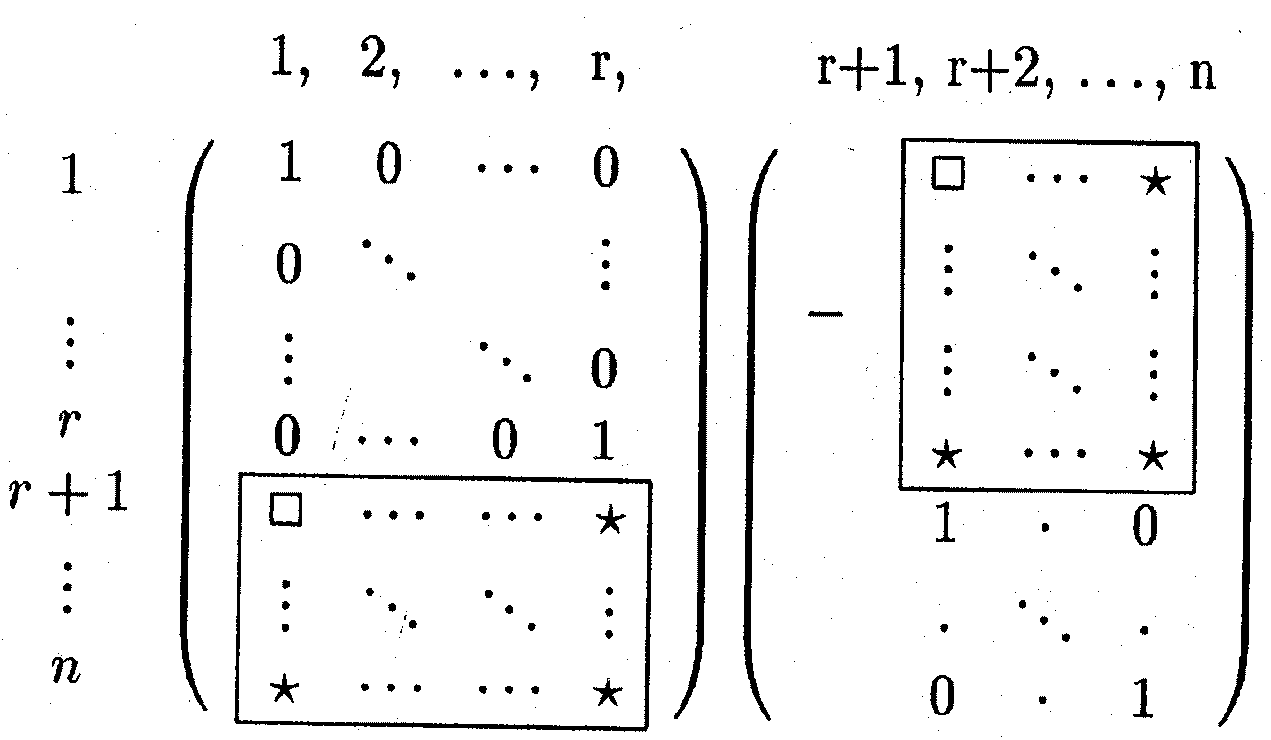
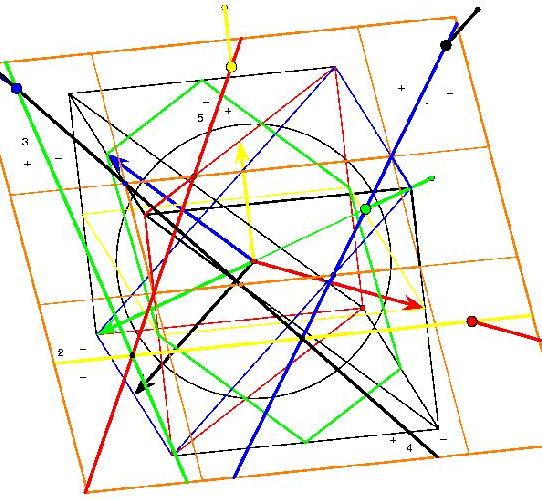
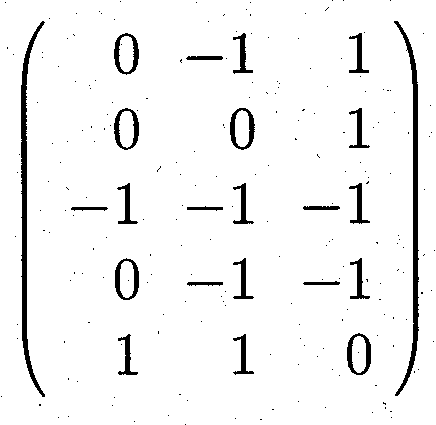
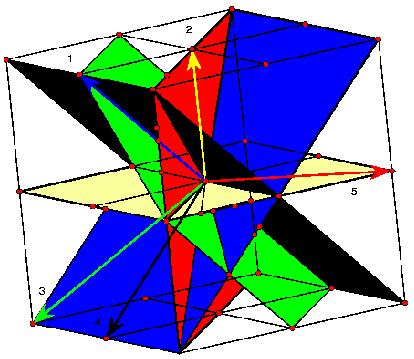
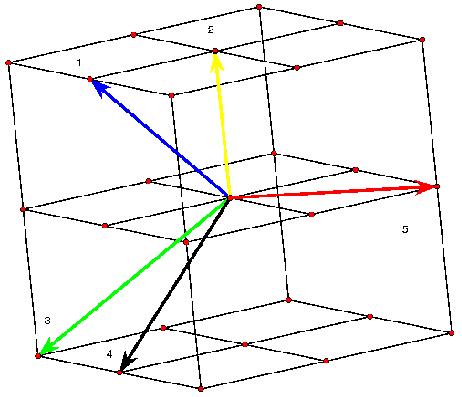
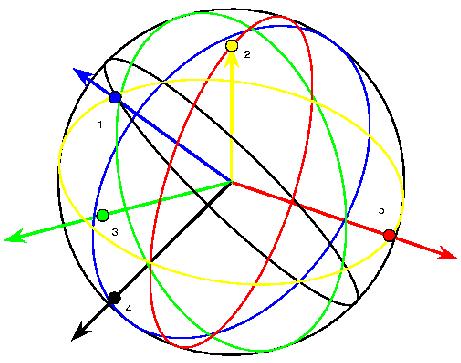
The following picture (the central part) shows the complete graph with 12 vertices on such a surface. This time the surface is more difficult to detect. There is a top triangle and a bottom one with adjacent 3 triangles each. 6 triangles form a cylindrical central shape. The next topological triangles (with curves instead of line segments) are part of the handles. Because of the symmetry they have to be inserted 6 times. Some of the boundary curves occur only 3 times because of the upside down symmetry. People still find it difficult to understand the shape of that model.

In order to find the result that the corresponding map has no polyhedral realization, the theory of oriented matroids has been applied, see the article by Bokowski and Guedes de Oliveira. A certain flavour of the theory of oriented matroids with its wide range of applications can be guessed when we look at the possible representations of a matrix. The following (5x3)-matrix can represent 5 vectors in 3-dimensional Euclidean space, or 5 central planes in that space. It can also describe 5 great circles on a 2-sphere or 5 points on that sphere. A tangent plane attached to the sphere tells us that we can reinterpret the matrix as a point configuration within that tangent plane or as a line configuration. But there are many more interpretations, the rows of the matrix generate a vector space, this in turn defines an orthogonal vector space etc.

When we think about the great circle representation of a matrix, we can understand that the following models show the vertex figure of an icosahedron on the one hand and Pappos’ configuration in the projective plane on the other.

This great circle representation of a matrix is close to the topological generalization of the equivalence class concept for matrices. We study simple central symmetric closed curves on the 2-sphere like in the two following examples.
 

These models together with the following pottery model shows the embryonic stage of a recent discovery of the author with T. Pisanski. Oriented matroids of rank 3 and complete graph embeddings on surfaces can be viewed as closely linked, see the cited article by Bokowski and Pisanski.