1 STUDENTS WORK

Before we display the items produced by the artist starting from the work of students (see the first previous part of this paper), we show in figure 1 an example of a work from the first group of students, made by hand, in black and white, and using just paper, scissors and photocopier.
 

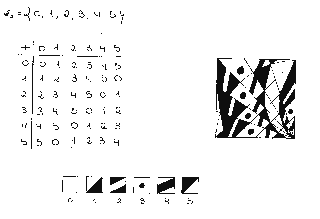
Figure 5 shows three examples from the second group of students, where a computer has been used, and additive and multiplicative structures can be identified. 
 

2 THE ARTIST WORK

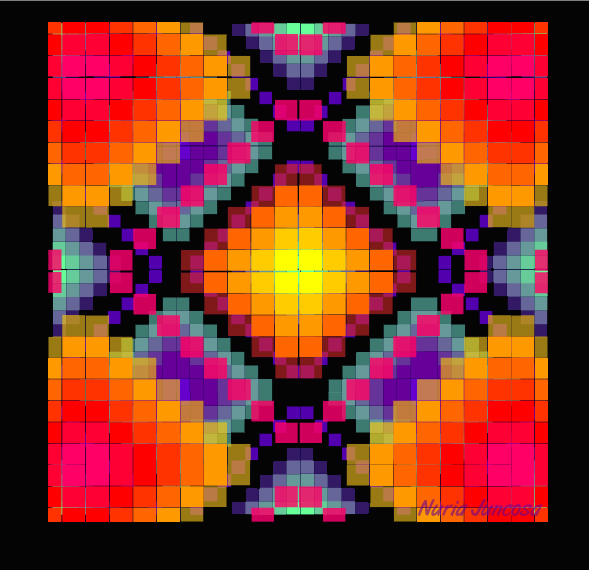
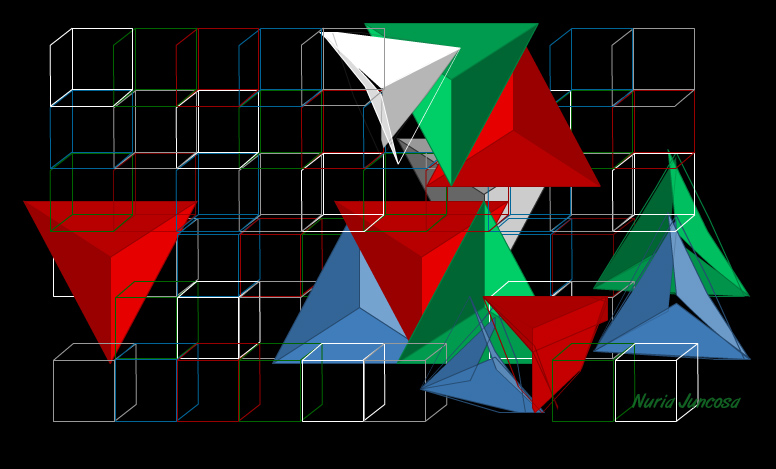
I am a visual artist, a painter and a cinematographer. I use to make movies and I paint pictures using oil to make my works, but I never worked within the world of abstractions before this experience in contact with mathematics.

After discovering a new dimension in art, through computers, I started using Flash to make animated art movies to place them on internet. I was very interested in experimenting new shapes and colours by means of computer, and I thought that I could use numerical patterns for this purpose. But I am an artist and not a mathematician. I wondered if I could find a system to obtain such patterns in order to use them to achieve new shapes. 

Fortunately I exchange several emails with Francisco Ruiz, and he explained to me how to generate some patterns, using mathematical concepts. A few months after I met him in Granada and I had the opportunity to talk to him personally about using mathematical elements to create visual art. Then, I learnt what congruence is and that it is a good source of producing patterns. 
 

In this way I was more interested in knowing about mathematic structures, and I learnt to replace traditional symbols of numbers with several kind of geometrical objects. I produced many kind of interactive and non-interactive movies using Flash program, and I also have used multiplicative and additive structures, with different modules, different colours and shapes to obtain nice results. 

Discovering geometrical transformations helped me in my tasks, and in this way I played with rotations, translations, mirror symmetries, and even plane tessellations. 

Sound was another ingredient in my work, and I introduced it in my movies following some mathematic criteria.
 

I made not only virtual works but I also painted some canvas with oil, using the same rectilinear and algebraic structures, but with organic forms instead of geometrical ones, obtaining surprising results like beautiful landscapes and conceptual abstractions. 

In this section I show some of my works made with the help of different mathematical elements. They are static pictures taken from my movies.
 
 

3 CONCLUSIONS

In this work (written in two parts) we show a sort of evolution of the same idea of using the mathematic concept of group in order to generate artistic designs. In a first step students could take a contact with those basic algebraic elements by utilizing paper, scissors, photocopier. Then the same experience revealed how students can improve their products getting much more motivated to make connections between Mathematics and Art by means of computers. Finally we have the point of view of an artist, not linked to the world of teaching Mathematics. She found a useful tool: to use such numerical patterns and congruence in order to incorporate them in her work.
 
 

REFERENCES