1 THE TWO REALMS OF THE Large Glass

The Bride Stripped Bare by her Bachelors. Even by Duchamp, commonly known as the Large Glass, is one of his fundamental works. In four main collections of written notes, (Sanouillet, Matisse) Duchamp described the project and his concern with geometry. Two parts constitute the Glass. The higher part is the Bride realm. It is intended to be a 2D rendering of a 3D shadow of the 4D Bride (Cabanne, p.40). Duchamp (Sanouillet, p. 83) points out that in this realm objects lose "all connotation of men-surated position". The lower part is called Bachelor apparatus and is located in 3D a environment. It is a complicate machinery drawn according to a single-point perspective. Its forms are "imperfect" with respect to those of the Bride, because they are "mensurated". Thus the note opposes the 3D metric space of the Bachelor utensil and the emancipated 4D topological space of the Bride. The Bachelor can only try to emulate the spatiality of the Bride, also according to his more general effort of joining with her. Duchamp’s perspective is no longer realistic but rather scientific and focused on dimensions (Cabanne, p.38). Based on the blueprint of the project (containing the exact measures of each part of the apparatus), I checked the perspective of the Glass, showing that it is absolutely canonical and perfectly carried out (Giunti).
 

2 ROTATING THE LARGE GLASS

Dynamic geometry software (Cabri Géomètre) allows to move the apparatus, in order to show that a mix of rotatory motion, transparency and perspective can emancipate the spatiality of the Bachelor, by either adding an imaginary 4^th dimension or providing parts of the apparatus with unexpected topological properties. 

Most of Duchamp’s notes of the White Box (Sanouillet p.74-101) work by analogy, i.e. by observing what happens passing from 1D to 2D, from 2D to 3D, and then extending the outcomes to 4D. An example: to superimpose two chiral 2D objects a rotation into the third dimension is needed, hence two chiral 3D objects can be superimposed only by rotating into the 4^th dimension. Duchamp put it into practice (Adcock, p.177) in a preparatory study on glass, entitled Glider Containing a Water Mill (in Neighbouring Metals) of 1913-15. A semicircular panel of glass can rotate about its hinge. The panel contains the perspective drawing of a part of the Bachelor machinery called Glider. Due to its transparency, when rotated by a half turn, the Glider appears under its chiral version. Thus we have the suggestion of a turn into the 4^th dimension. The same effect of reversing the whole Bachelor apparatus can be obtained by walking around the actual Large Glass, swapping the roles of Glass and Observer in the relative motion. 

Duchamp largely used the analogical reasoning, but he perceived it unsatisfactory and rather sterile (Sanouillet, p.92). Hence he tried other possible ways, like for the Sieves. They are seven conic filters disposed in semicircle. Duchamp left a sketch containing their perspective construction. Once the ellipse at the base of the first cone was traced, he simply rotated it using a set of eccentric circles. The Sieves were intended to force the Spangles (particles of frozen gas) in a circular course, and the circles used for the perspective construction can be seen as their trajectories. Now, if we hold the Spangles still rotating the circles (maintaining the relative motion as done above), we gain an amazing outcome: due to their eccentricity, the rotating circles give us a very impressive stereokinetic effect. Thus the plane gives the illusion of a volume. But, according to the perspective metaphor, we virtually have the illusion of a hypervolume. Only speculations? Possible, but this is exactly what Duchamp did a few years later with Anemic Cinema (1925) and the Rotorelief (1935). Passing through this "labyrinth of the three directions" the Spangles "imperceptibly lose […] their designation of left, right, up, down, etc, lose their awareness of position" (Sanouillet, p. 49); but, for Duchamp, similar swaps left-right, up-down are always related to the 4^th dimension. Related to those swaps there is another interesting feature. The preparatory sketch of the Sieves with its semicircles, actually depicts a semi-torus. The loss of distinction left-right or up-down also means identification. Now, it is well known that by identifying any pair of its symmetrical points (with respect to the centre of the torus), one obtains a Kleinian bottle, whose counterintuitive properties, especially the loss of meaning of inside and outside concepts, emulate the emancipated properties of the Bride realm space. 

Geometrically speaking, the most interesting device of the Bachelor is the Chocolate grinder. Three conical frusta (the rollers) rotate (with a sliding component) on a conical chassis. The roller are carefully ruled with threads, as the coiling of a dynamo. This connects the Grinder device with electromagnetism, as definitively documented by Henderson. But Duchamp also spoke of the threads in terms of "generatrices" (Matisse, entry 36). Accordingly the Grinder is a very effective generator of ruled surfaces. This is fully consistent with Duchamp’s theory of "elemental parallelism" (Adcock, pp. 137-199) and with his interest in Marey’s chronophotography (Cabanne, p. 34). Supposing the Grinder at work, we obtain several ruled surfaces as geometrical loci of the threads. When the rollers slide without rotating around their own axes, the loci of the diametric threads are single-sheeted hyperboloids, which are actually mentioned by Duchamp (Sanouillet p. 83) as examples of geometrical objects which "lose all connotation of men-surated position" by passing into the Bride realm. Single-sheeted hyperboloids can be used to create a special type of gearing, very similar to that one depicted in the Coffee mill (1911). Even more interesting and complicated bands, belonging to the family of the Moebius strips, can be obtained as the loci of the threads (of both the slant heights and top or bottom diameters) under the assumption that the rollers also rotate around their own axes, while rotating around the Grinder axis. Again, rotation allows the Bachelor to emulate the topological essence of the Bride space.
 

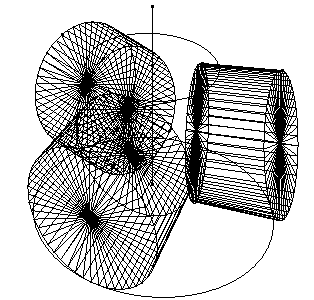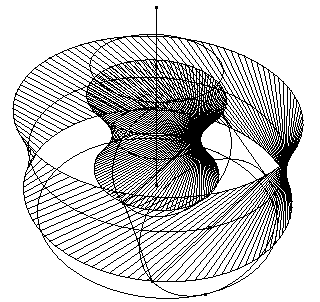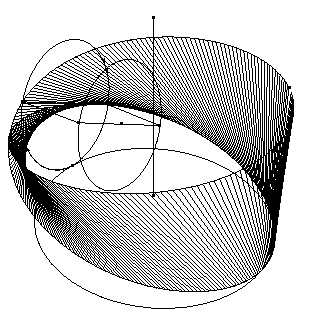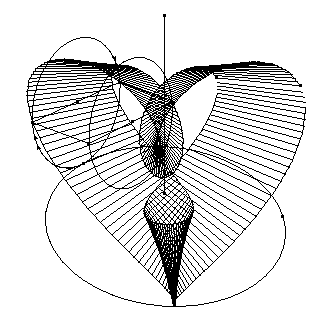
Finally let us consider the Water mill wheel contained in the Glider. The rotation of the wheel was combined with the onanistic left-right sliding of the whole Glider (Sanouillet, pp. 56-59). While I was working with Cabri to rotate the perspective drawing of the Water Mill wheel, I serendipitously discovered a surprising effect. I filled the eight paddles of the wheel with a grey solid colour, to better appreciate their rotation. But, the filling order followed by Cabri to repaint the successive frames of the animation is that followed by the User to create the animated objects, and not that consistent with the perspective system. Hence, in the animation, from time to time it happens that the paddles can be painted either according to the correct foreground/background policy or not. In turn this causes continuous and unexpected (but stable) swapping in the perception of the rotation, either clockwise or anticlockwise. In turn, this causes a marked Necker-cube effect in the overall perception of the Glider, as if it were seen from either left or right, which finally is fully consistent with its projected onanistic motion. What is quite amazing now, is that even if the paddles are drawn transparent, one easily learns to perform stable mental inversions (clockwise or anticlockwise) if and only if the device is rotating. Of course similar perceptive swapping into chiral instances of the same object are connected with rotations into the 4^th dimension. Hence, even if the Bachelor is not as emancipated as the Bride, at least he is clever enough to find some remedies. 

The main objection one could make against what I presented here, is that the actual Glass is in fact definitively and dramatically static, which of course is true. There are no special or magic effects in looking at the Glass. But what one has to bear in mind is thinking of the Glass, which was strongly recommended by Duchamp, by stating the primacy of the grey matter over the retina (Cabanne pp. 38-39). Duchamp said that his notes must be considered as essential parts of the very Glass (Cabanne, pp. 42-43). The Glass was conceived in perpetual and ubiquitous motion, with a particular inclination for circuital courses. Duchamp made clear his attraction for circular motions (Tomkins p. 125). Furthermore, we have several notes where Duchamp points out the importance of relative motion (of subject and object) in the perception of space (Sanouillet, pp. 87-88). Thus, Duchamp suggests us to move the Glass with our mind. The second point to make clear is whether or not Duchamp imagined something similar to what I presented above. The example of the hinged Glider is self-evident. The stereokinetic effect discussed with the Sieves, will be actually exploited a few years later (that’s why I consider the perspective study of the Sieves as the most relevant antecedent of the successive optical devices). For the rest we have only clues which make us suppose some possible awareness of Duchamp. He actually cited quadric surfaces, but not with direct reference to the Grinder. Clair confirmed that Duchamp knew Kleinian bottle and Moebius band but not referred to the Grinder or to the Sieves. The strange reversible motion of the Water Mill is actually consistent with Duchamp’s notes, but there is no evidence that Duchamp exactly thought of something similar. Anyway, at least we can say: Duchamp suggested us a recipe (mix perspective and rotations); and, when we use it, it works perfectly. 
 
 

References