| 1
Introduction
|
|
|
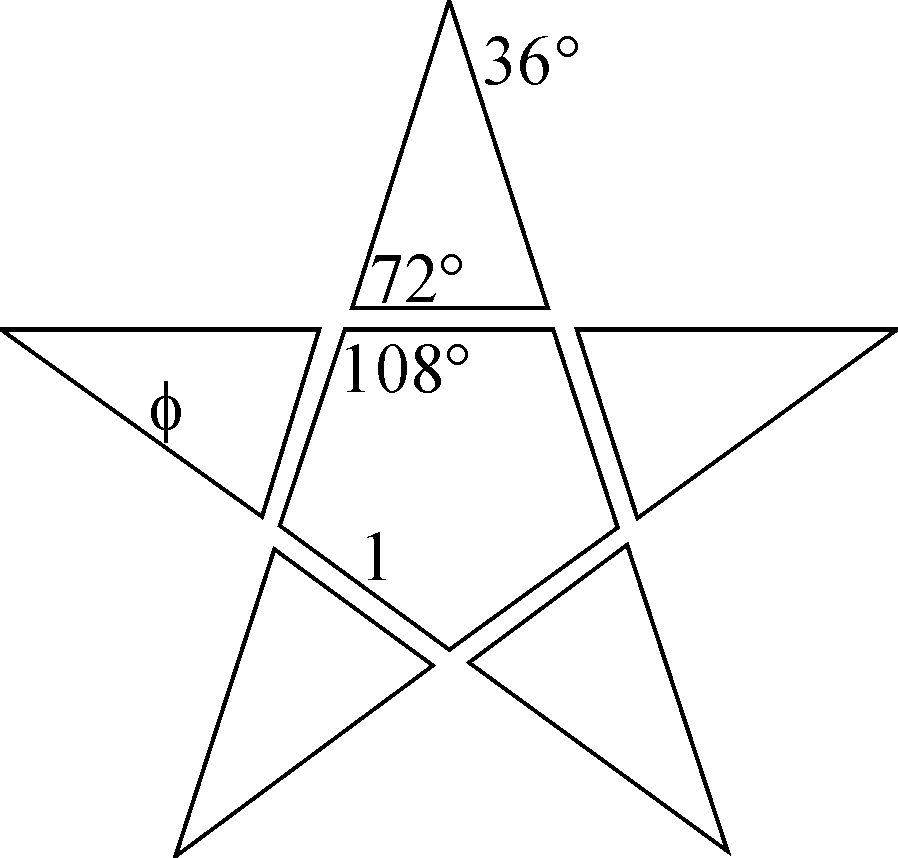
Following Euclid’s "rule", the golden number (or golden
section, mean, or ratio, or divine proportion, etc.) arises when a line segment
of length f
= (1+√5)/2»
1.618… is divided into two pieces of lengths 1 and
0.618… In the regular pentagonal star and the "regular" pyramid, the
golden number is discovered too (see Fig. 1). These numerical properties got
numerological interpretations in mythical circles, in as much that the
denomination of "golden angle" of 36° was introduced in literature. Furthermore,
since the proportion of consecutive Fibonacci terms 1, 1, 2, 3, 5, 8, … tends to
f, the
occurrence of f in many unpretentious proportions of 2 to 3, 3 to 5
and so forth is not surprising. In recent times, several authors pointed out
that the occurrence of the golden section in Egyptian pyramids, Greek art, da
Vinci’s work, in music, poetry, modern architecture and art must be considered
with the greatest precaution. Most of these "justifications of the frequent
occurrence" of the golden number do not relay on solid backgrounds, while their
frequency depends on a personal interpretation.
|
|
|
|
|
|
The’ regular’ pentagonal star and Utah piramid with height = base×√f /2. |
|