|
JÜRGEN BOKOWSKI
1 COMBINATORICS OF TORI OF CSÁSZÁR
AND SZILASSI
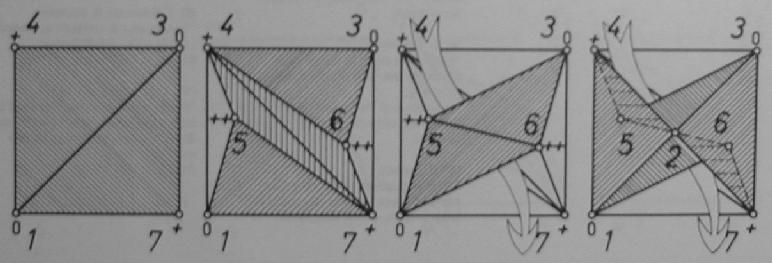
From a square with diagonal (1,3)
we lift vertices 4 and 7. Insert 4 triangles as shown. Points 5 and 6 lie
higher than all previous ones. Add two additional triangles. An apex above
the midpoint of the original square together with a roof structure of additional
6 triangles tells us the shape of the torus of Császár.
Szilassi’s torus is shown on the right with its seven non-convex
facets. Both polyhedra have a geometrical symmetry of order 2. This is
optimal, see Bokowski and Eggert 1991 and Bokowski and Schewe 2004.
Figure 1: Császár.’s torus (left) and Szilassi’s torus (right). Let us study its combinatorial symmetries.
Look at the ring surface depicted as our first pottery model. Six curved
edges start at each vertex reaching all the remaining vertices. This complete
graph embedding published Möbius
in 1861.
Figure 2: From left to right: Möbius’s torus, Heawood’s map, Curve arrangement. We place a vertex in each curved triangle
and we connect vertices when the corresponding triangles have a common
edge to obtain Heawood’s map, see a nice model of Carlo Séquin
in the middle. Both combinatorial objects are regular maps.
Figure 3: Cuve arrangement on a surface of genus 3. The related pottery object of the author on the right shows seven simple closed curves on a genus 3 surface. The two parts of each curve with a common colour have to be connected. We identify seven pairs of edges of the regular 14-gon when the same pair of curves meet and in such a way that the curves cross. Each pair of curves has precisely one intersection point. The next pottery model shows the curves on the surface. The surface hides the symmetry, however, it reveals the additional combinatorial symmetry of order 3. The combinatorial symmetry group is known to be of order 42. We have seven points in Möbius’s
torus, seven cells in Heawood’s map, seven curves on the genus 3 surface.
Any two points are joint by an edge in case of Möbius’s
torus, any two cells have an edge in common in Heawood’s map and any two
curves have a common intersection point. The incidence structure in all
three cases is identical. This is indeed the starting point for a transition
from graph embeddings on surfaces to curve arrangements on surfaces. The
case of simple closed curves in the projective plane lead to the theory
of oriented matroids, see Björner
et al. 1993 and Bokowski, 2005.
2 ON OTHER SPATIAL POLYHEDRA WITHOUT DIAGONALS There are other triangular complete
graph embeddings in great profusion. However, not a single example out
of infinitely many of them has been realized as a polyhedron.
Figure 4: Complete graph with 12 vertices on a surface of genus 3. Imagine that the next smallest case
looks already somehow like the above K12 embedding on a genus 6 surface
with 44 triangles. Bokowski and Guedes de Oliveira have shown that in this
particular example a search for coordinates such that the polyhedron has
no self-intersections will be in vain. A corresponding polyhedral realization
can simply not exist. See additional comments in Bokowski 2001.
3 4-DIMENSIONAL POLYHEDRON WITHOUT DIAGONALS In dimension four there are convex polyhedra without diagonals for any given number of vertices. A Haskell code (functional programming) exemplifies the case with 8 vertices.
4 SPATIAL PINCHED SPHERES WITHOUT DIAGONALS There are spatial polyhedral realizations
of pinched spheres that have no diagonals, see Altshuler, Bokowski, Schuchert
(1993) and (1994).
References Altshuler, A., Bokowski, J., and Schuchert, P. (1993) Sphere systems and neighborly spatial polyhedra with 10 vertices, Proceedings of the First International Conference on Stochastic Geometry, Convex Bodies and Empirical Measures, Palermo, Italy, Supplemento ai rendiconti del Circolo matematico di Palermo, Ser. II, No. 35, 1994. Altshuler, A., Bokowski, J., and Schuchert,
P. (1994) Spatial polyhedra without diagonals, Israel J.Math., 88,
373-396.
Altshuler, A., Bokowski, J., and Schuchert,
P. (1996) Neighborly 2-manifolds with 12 vertices, J. Comb. Theory,
Series A, 75, No. 1, 148-162.
Bokowski, J. (2001) Pottery models and
complete graphs on surfaces, Symmetry: Art and Science,Proceedings of
the Sydney Congress of ISIS-Symmetry.
Bokowski, J. (2005) Computational
Oriented Matroids, Cambridge University Press, to appear.
Bokowski, J. and Eggert, A. (1991) All
realizations of Möbius’ torus with 7 vertices, Structural Topology,
No. 17, 59-78.
Bokowski, J. and Guedes de Oliveira,
A. (2000) On the generation of oriented matroids, Discrete and Computational
Geometry, 24, 197-208.
Bokowski, J. and Pisanski, T. (2001)
Oriented matroids and complete graph embeddings on surfaces,J. Comb.
Theory, Series A, submitted.
Björner, A., Las Vergnas, M., Sturmfels,
B., White, N.,Ziegler, G. (1993) Oriented Matroids, Cambridge:Cambridge
University Press
Czászár, Á.(1949)
A polyhedron without diagonals, Acta Sci. Math. Universitatis Szegediensis,
13, 140-142.
Lutz, F. (2002) Czászár’s
torus, Electronic geometry model, No. 2001.02,069.
Ringel, G. (1974) Map Color Theorem,
Springer, Berlin, Heidelberg, New York.
Szilassi, L. (1977) Egy poliéder,
melynek bármely két lapja szomszédos, Juhász
Gyula Tanárképz?F?iskola Tudományos Közleményei,
2, Szeged, 130-139. (In Hungarian.)
Szilassi, L. (1986) Regular toroids,
Structural
Topolgy, No. 13, 69-80.
Additional note: Möbius's
torus and its dual, the Heawood map are no regular maps in the strongest
sense.
|