




 |
 |
 |
 |
 |
 |
Research findings suggest that relative motions can be used as an interesting way to generate complicated forms. In the world of computers where Newton's Law of Gravity does not apply, we were able to set our own arbitrary rules of motions to experiment with trajectories never existed before. It has always been interesting to observe how the images might turn out to be when the level of relative motion increases.
A quick decision must be made when an image was finished: Whether to keep it or not? The decision was rather subjective. The image was kept if it looked nice, and dumped if not. It made us wonder what the standard should be. It seemed that the ones we preferred all shared one characteristic, that is, certain kind of mixture of order and disorder, or complex and simplicity. Could this be a loose definition of the beauty of this kind of forms? That is the question we need to contemplate in the future.
We often obtain an image with circular outline. Although the shapes are not so astonishing, we still keep them. This kind of shapes sometimes have interesting patterns embedded in them.
Color palette is another subjective issue. An image may look quite different with different palettes. However, it is difficult to determine the optimal palette for any given image. Maybe there should be an easy way to switch the palettes, so as to provide more alternatives.
When chaotic factors are added, the trajectories usually became dramatic and sometimes even peculiar. Any slight variation of the initial state might result in entirely different outcome. The trajectories of these kinds of relative motions tend to be highly unpredictable. On the other hand, pursuit curves seemed to be another interesting way to create forms. They both call for further explorations.
We experimented on an interesting kind of chaotic relative motion. We made an assumption that is impossible in the real world: the earth orbits the sun, and the moon orbits the earth, and the sun orbits the moon. In order to limit the trajectory to our computer screen, we discover to increase the angular increment among coordinate systems and decrease the radii among coordinate systems. It is unpredictable when the relationship among coordinate systems is chaotic. We could increase the level of coordinate systems, there can be of course, and the images created can hardly be imagined. For instance, there are six coordinate systems, A, B, C, D, E, F, and the relationships of them are A->B, B->C, C->D, D->E, E->F, and F->A. The symbol “->” here represents the movement of orbits.
When the angle of coordinate system is increasing or decreasing as a variable of time, the shapes created are sometimes overwhelming. The velocity of relative motions is according to the variation of angle, and even change the clockwise or counterclockwise of relative motion. Firstly, we experiment a spiral movement that angular increment dA is fixed. Then, we attempt to experiment the different parameters of angular movement. The ceiling-limited and floor-limited value of angular movement is among 0.16 and -0.48 angle. The radius increment of spiral movement is 0.01 pixels, and radius is 150 pixels. The increment of angular increment is a variable, this example ddA, and we will show the different results.
| Table 4-1 the different dA (30,000 iterations) | |
|
dA = -0.48  |
dA = 0.16 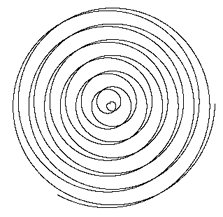 |
| Table 4-2 the different ddA (dA = 0.16 ~ -0.48; 30,000 iterations) | ||
|
ddA = 0.0001 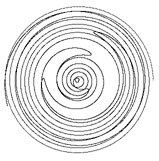 |
ddA = 0.0005 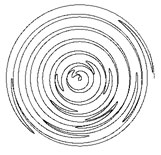 |
ddA = 0.0007  |
|
ddA = 0.001  |
ddA = 0.002  |
ddA = 0.003  |
We adopt the pursuit concept in these kinds of relative motions. The trajectories of pursuing a target object are interesting. We increase the systems of multi-level relative motions, and the trajectories are unpredictable and somehow peculiar. There are two kinds of rules in pursuit relative motions: (1) always pursue the nearest coordinate system, and (2) always pursue the furthest coordinate system. The two kinds of pursuit relative motions lead to different results. We may set the rules that the trajectory pursue the coordinate system of the proportion among two coordinate systems. For instance, the trajectory are influenced from two coordinate systems, A and B, and the degree of influence is different from them. The pursuit velocity among coordinate systems is also a crucial factor. This new concept may result in another interesting images.
The another pursuit relative motions are according to some rules to record the trajectory of coordinate system. For instance there are two coordinate systems (A and B). If the distance of the trajectory and B is more closer to A, the trajectory will be switched to the A, and contrariwise. We could add the chaotic terms into the coordinate systems, and the results are very different.
It has always been an amazing experience to watch unseen images gradually unfurl themselves. We defined the motions and we set all the parameters, and yet we still could hardly predict the trajectories. Forms seemed to grow merely by themselves. As creators of these images, we realized that we actually had little control over them. Ironical as it may sound, this is the pleasure of creating forms. We will show some the evolutions of relative motions with different parameters. Maybe we could find some rules in these inductions of testing parameters.
CONTENTS:
| Conclusions |