SCHULZE-FIELITZ

The systematization of space is a condition for the spatial composition of standardized parts, and thus the basic tenet in prefabrication.

Modular coordination offers, in spite of the strictest systematics, great freedom in selection and arrangement, and thus for the synthesis of the tendencies of commercial mass-production and individual multiplicity. The interchangability of spatially coordinated quantums achieves flexibility and adaptation in dynamic developments. Geometry, topology, group theory and combinatory methods are going to influence serial constructions in architecture.

The spatial structure is a macromaterial capable of modulations, analogous to a hypothetical model in physics, according to which the multiplicity of manifestations can be reduced to a few elementary parts. The physical material is a discontinuum made up of whole-part units, molecules, atoms, and elementary particles. Their combinatory possibilities determine the properties of the material used. Not until we have a modulation of spatial structure is there a discontinuous continuum, discontinuous due to the marking line between a part and its whole, and continuous due to the unchangable possibilities of change.

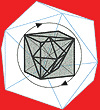
In 1959, Schulze-Fielitz combined the space-filling intracubic Platonic solids, cube (1), tetrahedron (Ö2) and octahedron (½ Ö2), and introduced the spatial diagonal (Ö3) into the cube. As a rectangular prism, the cube is the habitable element in this crystalline spatial structure, resulting in the theoretical proposition of a continuous spatial city capable of growth in all directions.

Schulze-Fielitz also introduced the a, b and g positions of crystalline structures, which recognized all lattices known at the time as different sections taken from the same spatial structure. With the discovery of the Metaeder as a combination of all regular polyhedrons, i.e. plus the extracubic, non space-filling solids as well, a further position called d was introduced, which is of determinatory importance for the position for the Fuller domes principally constructed on the icosahedron (j) and the dodecahedron (1/j).

With these additional possibilities, the structure also shows five fold symmetries, which were neither present nor possible in the spatial structure of crystals; they also include now the quasicrystals with Kepler's thirty-faced rhombic triacontahedron as elementary cell and its two-dimensional counterpart, consisting of two different rhombuses (als "tiles") having a five-numbered symmetry in each case; furthermore, the harmonic rectangle 1/j with its close relationship to the number five [j =(1+Ö5)/2], any number of progressive or harmonic series, the logarithmical spiral or Spira Mirabilis with its "self-similarity" as important criterion for fractals and the starting point of fractal geometry, by Mandelbrot. The "crystalline" structure stands on a, b or g, the quasicrystalline on d.

The following shows a series of examples for structural architecture in projects and realisations.