QUASICRYSTALS IN THE METAEDER

In addition to the regular "Platonic" solids already known to the Pythagoreans and described by Plato — the semiregular "archimedean" polyhedrons ascribed to Archimedes — and the non-convex star polyhedrons Johann Kepler discovered and described, he also found two rhombohedrons: the twelve-sided one with its periodic space-filling property, the so-called rhombic dodecahedron, and the thirty-sided triacontahedron, non-packable solid with its five fold symmetry in d, which according to then accepted opinion, does not make a periodic filling of space possible. Both are contained in the Metaeder.

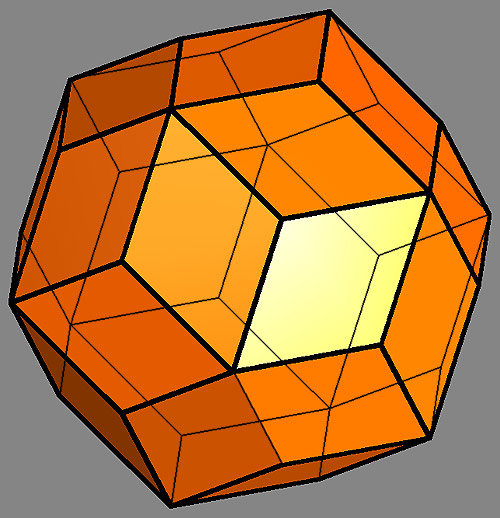
The first is generated via quadratic pyramids on the sides of a cube, the second via three-cornered pyramids on the sides of an icosahedron. The d-position of the rhombic triacontahedron produces an aperiodic surface tessalation, a Penrose pattern - its corresponding forms in space are the quasicrystals discovered by Shechtman in 1984.

Quasicrystals are formed either by the overlapping arrangement of rhombic triacontahedrons or by the aperiodic / complementary packing of rhombohedral solids, all of whose faces are formed with golden rhombuses: two different rhombohedrons, the rhombic dodecahedron, the rhombic icosahedron and/or the rhombic triacontahedron.

This is in fact a classic quasicrystal which, in the d projection, generates the classic Penrose pattern.

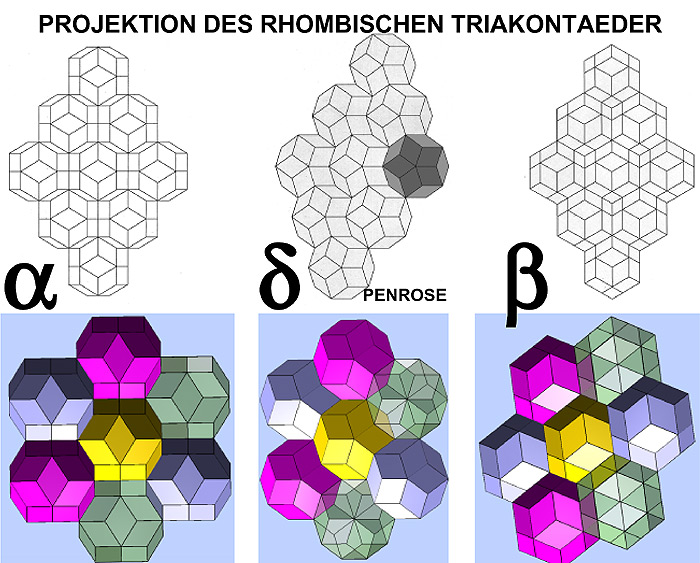
A two-dimensional projection in d of the rhombic triacontahedron results in the so-called Penrose pattern.

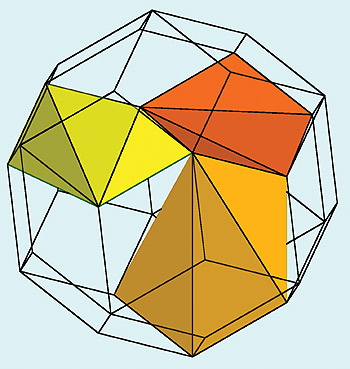
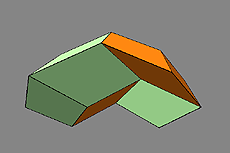
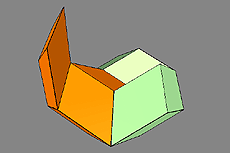
Another frequently published Penrose pattern consisting of three pentagons, two rhombuses and a crown produces, as a corresponding spatial form, the figure shown below.

Quasicrystal

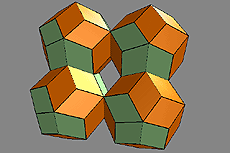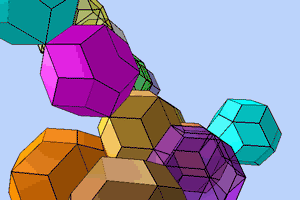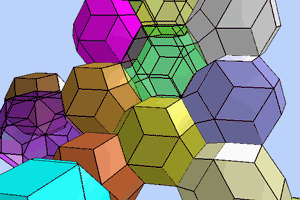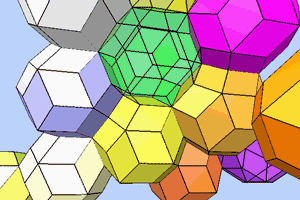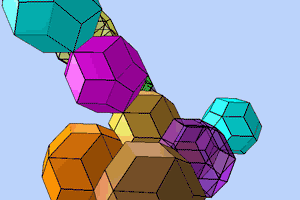
The unit cells of a quasicrystal are two different complementary packable golden rhombohedrons, an acute-angled (brown) and an obtuse-angled (green) one, whose sides form golden rhombic figures. These rhombohedrons can be combined in a space-filling manner to form rhombic dodecahedrons, icosahedrons, triacontahedrons and, over and beyond this, quasicrystals. All figures are contained in the Metaeder.