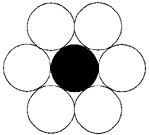
An interesting measure of the size of a circle is the possible number of neighboring circles. One can place circles in a rectangular grid, with identical circles touching above, below, to the left, and to the right of the central circle. However, a tighter arrangement can be made, with hexagonal symmetry. Here, each circle is surrounded by six equivalent ones. This arrangement has the special property that all the neighbors are touching two other circles off the original one. In other words, six circles will exactly surround one, in two dimensions. Items forced on to a flat surface, if short on space, will get six neighbors, and tend to take on the shapes of hexagons themselves, as in a honeycomb (Figure 18).

Another example of the kissing number in a plane is carbon atoms in graphite, as in pencil "lead" (Figure 19). Here, layers are made of carbon atoms forming three bonds in the plane to similar atoms. The atoms form flat hexagonal rings, which are surrounded by identical hexagons.
 

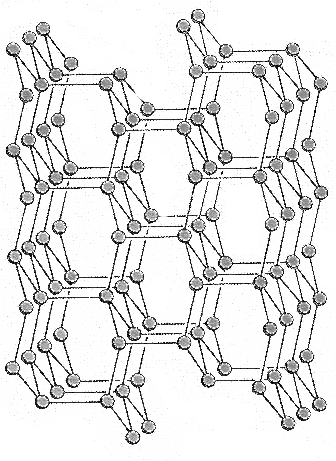
While carbon in the graphite form is essentially a two-dimensional structure, the diamond form of carbon is a covalent network solid, extending equally in three dimensions (Figure 20).
 

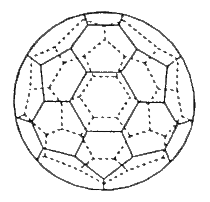
In the last few years, a third fundamental form of the element carbon has been discovered, in which individual atomic bonds are made in two dimensions, but the overall shape obtained is three dimensional. Specifically, a group of 60 carbon atoms will wrap itself into a sphere (changing some hexagons into pentagons). This forms a compound called buckminsterfullerene, or a buckyball (Figure 21). This is named after the inventor of the similarly shaped geodesic dome, Buckminster Fuller.
 

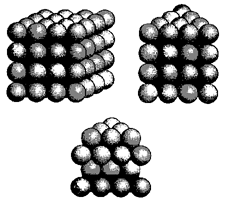
The problem of stacking or packing balls efficiently has been an interesting puzzle for four centuries. While people have stacked things for millennia, it was in 1611 that Kepler posed the Sphere-Packing Problem [19]. What kind of stacking of spheres can be proven to be the densest possible?

A first layer of spheres can be arranged in the rectangular or hexagonal patterns of circles in a plane, described above. Such layers can be stacked exactly atop one another, yielding respectively the arrangements called the body-centered (or 3-dimensional) cubic lattice, and the face-centered cubic lattice or cubic close-packed form (Figure 22). However, if flat layers are stacked repeatedly in a staggered way, a third, most dense pattern emerges, called the hexagonal lattice, or hexagonal close-packed [20].
 

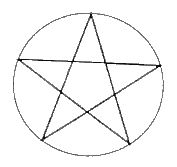
All three of these packings are found in nature, as are mixtures of these with less regular forms. Interestingly, elemental metals use all forms, in patterns that do not always correlate with electronic symmetry. For example, potassium, chromium and tungsten prefer the body-centered cubic form, as does iron at room temperature. However, iron at other temperatures takes on the cubic close-packed form, as do copper, silver, and gold. In contrast, the elements in the same period directly below iron (i.e., ruthenium and osmium) prefer the hexagonal close-packed arrangement, as do most of the rare-earth elements, as well as zinc and titanium [20].

The number of circles that can surround a circle in any given dimension is called the "kissing number" by mathematicians. On a one-dimensional line, this is two (left and right). In a two-dimensional plane, as we discussed, the kissing number is six (see Figure 18). The kissing number is 12 in three dimensions, as in the above hexagonal close-packed arrangement (with six in the plane, three more above, and three others below). In theory, a four-dimensional sphere should have a kissing number of 24, in eight dimensions it is 240, and in 24-dimensional space the kissing number is 196,560 circles touching the center circle at once [19].

The kissing number of six for a circle means that it is possible to construct a regular hexagon (and consequently a six-pointed star) by using the radius to cut the circle into six equal arcs. Unlike the simplicity of the construction of a six-pointed star, it is a challenge to use only a compass and straight edge to construct a pentagram, a five-pointed star extending from a regular pentagon.

To do this task, we need to know how to find the "Golden Mean" of a line segment. The Golden Mean is a cut in a line segment such that the ratio of the larger section to the smaller one is the same as the ratio of the entire line segment to the larger one. It is possible to find the Golden Mean of a given line segment using a compass and straight edge. The Golden Mean has been used extensively in art and architecture from the ancient times of the Egyptians and Greeks up to today.

The larger section of the Golden Mean of the radius of any circle divides the circle into ten equal arcs, which enables us to construct the pentagram [21]. The complexity of these procedures, or the harmony and order of the completed form, created the association of mysticism with the combination of a pentagram inscribed in a circle, the chosen symbol of the order of the Pythagoreans, sometimes associated in western tradition with witchcraft (Figure 23).

The word Sama means the joyous but ceremonial religious excitement of the Sufi faithful, either individually or together. Today, it also is any of the famous whirling and circling dances done to the lamenting reed pipe and the pacing drum, performed by the Mevlevi dervishes. These are the disciples of the Sufi poet and spiritual leader, Jalal al-Din Molavi al-Rumi (1207-1273). Rumi is, by one account, the best-selling poet in the United States today [22].

Rumi is one of the most well-known of the historical Persian-language poets, and his mystical poems have been sung from Afghanistan and India to Iran and Turkey for seven centuries. He feels a transcendent, romantic relationship and obsession with the creator, and equally with all of creation. He was born in Balkh (now in Afghanistan). The Mongol invasions caused his family to flee, while he was still a child, to Konya (now part of Turkey), where he lived and died.

Rumi was a theologian, preacher and conventional religious scholar through age 37. Then a man in his sixties arrived, a wandering dervish of wild demeanor named Shams al-Din, who transformed Rumi’s world view, despite resistance from Rumi’s many conventional religious pupils. Rumi’s new ecstasy with the world led him to express his feelings with poetry and with a revision and popularization of the whirling dances of the dervishes. He would even dance and sing to the sounds of the metalworkers in the bazaar.

The Sama, in the mystical culture of Persia popularized by Rumi, is demonstrated by a person under the influence of a deep, internal feeling of excitement and love for the spiritual beauty of creation. The person stands up, without feeling self-conscious, and starts circling and whirling. This is especially done according to certain conventions of hand positions and other dance movements that symbolize the spiritual attitude of the obsession with love of the universe. To this day, this is performed in Turkey every year for thousands of visitors, during the week around December 17, the anniversary of Rumi’s death.

The Mevlevi dervishes consider the space in the house of the Sama to represent a spherical form of the universe. An imaginary axis divides it into western and eastern pieces. At the center is a small circle, called the "pole." After music and singing to candle-light, the circle dancing is done as shown (Figures 24 and 25). The hands are open and arms extended. The right palm faces up to the spiritual sources of heaven, while the left palm faces down to the world, with the dervish’s heart in between, as a medium or bridge. The left foot is fixed, while the right foot causes the body to circle.
 

Figure 25. The circular dancing of a man inspired by Rumi’s philosophy, 
showing the same symbolic pose, but in a different costume and 
at a more intense part of the ceremony [23a].

Rumi’s poetry expresses circles in several different ways, such as in how he saw himself in the world [23b].