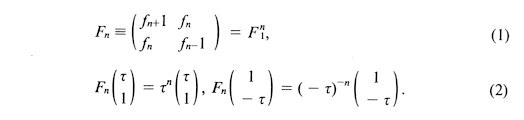|
AN ESSENTIALLY-THREE-DIMENSIONAL QUASICRYSTAL Tohru OGAWA Institute of Applied
Physics,
As the generator of an essentially-3-D quasicrystal, some detail of a 3-D Penrose transformation is given. The expansion rate t3=4.236 is by far the larger than ever believed value t=1.618. The features of this model agree rather well with those of high-resolution electron micrograph. The Penrose logic of hierarchic generation of patterns is summarized and a new expression is also given for 2-D Penrose transformation. 1. Introduction Crystallography is now in an epoch of revolution. It has been believed as established in the last century as the general system of possible configurational order. In that system, periodicity is the most important nature and any ordered configuration without periodicity is out of scope.Also in the electronic theory of solids, whose basis is Bloch theorem, periodicity is a priori assumed. The discovery of the sharp Bragg spots with icosahedral symmetry by Shechtman et al [1] is giving a shock to the system of configurational order in the above mentioned situation. It has long been known that icosahedral symmetry or, more generally, five-fold symmetry, is incompatible with periodicity. Some sensitive people felt some unsatisfaction in the classical crystallography excluding five-fold symmetry from rather aesthetic interest. For example, Husimi [2] had an idea of filling the inevitable gaps in a nonperiodic packing with regular pentagons of equal size. Among such attempts, Penrose [3] succeeded in a tesselation of a plane with two kinds of tiles closely connected with pentagon, basing on the logic of a recursive patterngeneration. His tesselation [3,6] is essentially nonperiodic, homogeneous, isotropic and self-similar in a sense. Along this stream of interest, Mackay [7,8] tried the generalization of this tiling to 3-D case. These efforts were paid before the exciting experiment by Shechtman [1]. After
the experiment, many people explore the concept of quasicrystal and its
structural image [9,10].
Most of them are based on the 2-D Penrose pattern. Very recently,
the present author [11] found a 3-D Penrose
transformation and pointed out some difference between 2-D and 3-D.
An essentially 3-D quasicrystal, as ideal as possible, can be generated
by the infinite-timerecursion of this transformation. The main purpose
of this paper is to give a detail of this transformation.
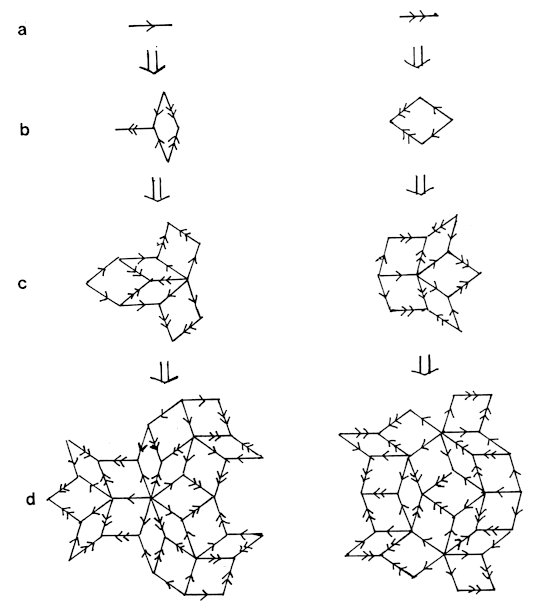
2. Penrose Logic In this section, the basic logic of generating an ideal nonperiodic pattern is summarized. It was originally introduced by Penrose in 1972 for 2-D case [3]. Prepare a proper initial pattern. Explicitly, in 2-D case, it is composed of two kinds of elements and must fill a certain condition. A pattern is transformed by a certain transformation rule for elements into another pattern which is also composed of the same two kinds of elements. This transformation is applied again and again. After infinite-time-iteration of this procedure, a whole plane is tiled with two kinds of elements. The pattern thus obtained is essentially nonperiodic and has some self-similarity or some hierarchic structure. Suppose a tiling of a plane with two kinds of tiles with properly designed figures on their face so that they are composed of miniature tiles of the same two kinds. Nonperiodicity is proved by the fact that a finite unit cell and a proper Bravais lattice can not be chosen since the composition ratio of two elements are irrational [5]. Here, a new expression of the 2-D Penrose transformation is given. In this version, the elements are two kinds of arrows. These two are the same arrows as introduced by de Bruijn [6] red arrows and green arrows of unit length, which, in prints in black, are indicated respectively with single arrows and double arrows. A set of transformation and an example of iterative transformation are given in Fig. 1. The plane gets tesselated with two kinds of rhombus whose sides are two kinds of arrows. The expansion ratio of this transformation is t. In the extension to 3-D, it is an easy way to imitate the 2-D pattern and to stack such layers in a sense. Isotropy, however, can not be expected in a 3-D pattern thus obtained. In order to find an essentially-3-D transformation if any, it is necessary to recognize the difference in nature of spaces in 2- and 3-D. For example, an n-gon has the same number of sides and vertices and generally an n-hedron has different numbers of vertices and faces. Such a difference of topological nature of space brings some hints to find an essentially-3-D transformation. What we should learn from the 2-D case is not the results but the spirit and the logic.
Fig.
1. New expression of a set of 2-D Penrose transformation and someresults
of its iterative operation.
3. Some Geometrical Preparations A golden rhombus is a rhombus the ratio of whose two diagonals is the golden number t; t= (1 + Ö5)/2 plays a key role in such problems as connected with five-fold symmetry. The rhombohedra whose faces are all golden rhombus are only two kinds A6 and O6. There acute vertices of three rhombi meets at a principal vertex in the former and three obtuse vertices in the latter. It is noted that these rhombohedra are consistent with icosahedral symmetry and a whole solid angle 4p can be composed only with these rhombohedra. It is also noted that the projection of a rhombic face of a golden rhombohedron onto the face normal to the third direction of the rhombohedron is either of acute and obtuse rhombi, the two elements in rhombic version of 2-D Penrose tiling. Some useful geometrical data on golden rhombus and these two golden rhombohedra A6 and O6 are summarized in Table 1. Any configuration constructed with only these two kinds of golden rhombohedra has bond orientational long range order since other nearest neighbour vectors never appear in a thus constructed "mono-quasicrystal" in the weakest sense than the twelves icosahedraly arranged. As a preparation for the discussion below, it is useful to introduce some terms and to see some typical configurations constructed with only A6 and O6. Some properties of them were studied by Miyazaki [12]. A
zonogon is defined as a 2p-gon with p pairs of parallel edges.
A zonohedron is a convex polyhedron made of zonogons. A golden isozonohedron
is a zonohedron whose faces are all golden rhombus. There are altogether
five golden isozonohedra; dodecahedron (12-hedron) B12, icosahedron
(20-hedron) F20 and triacontahedron (30-hedron) K30
besides two hexahedra (6-hedra) A6 and O6. All of
them can be constructed with only A6 and O6 in multiple
manners. This multiplicity is related with a kind of stereoisomer. A6
and O6 fill the condition as the 3-D tiles of quasicrystalline
configuration in a weak sense. Some properties of them are given in Appendix
A.
4. 3-D
Penrose Transformation
Golden
rhombohedra, acute A6 and obtuse O6 are chosen as
the two quasi-unit-cells of 3-D Penrose tiling as by Mackay [7,8].
By the 3-D Penrose transformation to be introduced in this section,
these two rhombohedra are transformed into two expanded rhombohedra which
are composed of only the two kinds of rhombohedra. The expansion ratio
is t3
which is the ratio of the length of the principal diagonal of A6
to that of O6. An expanded A6 is composed of 55 A6's
and 34 O6's and an expanded O6 of 34 A6's
and 21 O6's. These three numbers {21, 34, 55} are successive
terms of the Fibonacci sequence {fn; fn+1
= fn-1 + fn, f1
= f2 = 1} = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...}.
The corresponding three terms are respectively {1, 1, 2} in the original
2-D Penrose transformation and {1, 2, 3} in the 3-D version
suggested by Mackay [7,8].
The following matrices related with Fibonacci sequence are useful.
TABLE
1. Some useful geometrical data.
The
point a + t-1x
in the representation in Appendix B, dividing
the principal diagonal in the golden ratio, is equidistant from nine among
twelve midpoints of twelve edges. The distance is Ö(5-8t )/2
= 0.596.
*) A principal vertex of a rhombohedron is the vertex on the trigonal axis. A rhombohedron has two principal vertices. The principal diagonal joins them. An edge crossing a principal vertex is a principal edge. A rhombohedron has six principal edges.
The expansion rate of Penrose transformation is equal to the larger eigenvalue tn of the corresponding matrix Fn whose elements are {fn+1, fn, fn-1}. The present transformation consists of two parts; the skeleton part and other part. The transformation uniquely decides only the skeleton structure, leaving some degrees of freedom undecided in contrast with the completely deterministic 2-D Penrose transformation. One of the origin of this difference is the abundance of the symmetry operations in higher dimensions; 3-D rotation has more degrees of freedom than 2-D and there is the possibility of the so-called stereoisomer or the right- and left-hands freedom. All the rhombic faces have the identical skeleton structure. Therefore any two faces are fitting each other reminisce of the 2-D case; the sides of a rhombus are not simple segments but two kinds of arrows and are differently transformed. The coordinates of 102 quasi-lattice-points in the skeleton of an expanded A6 and 86 quasi-lattice-points in the skeleton of an expanded O6 are given in Appendix B in the form of six integer representation. The instruction for the model construction of the expanded A6 and O6 with sticks and ball joints is given in Ref. [11]. A skeleton of an expanded A6 consists of two empty triacontahedral cages overlapping each other and some acute-rich parts near the eight vertices of the expanded rhombohedron. It has some missing part around each of twelve edges. A skeleton of an O6 looks like a hexagonal snowflake, though the symmetry is trigonal as it should be. Around each of its edgess there is a missing part as in the former case. The following discussion generally holds. Suppose the situation that the symmetry of the outside of a zonohedron is rather high and that of its internal structure low. A configuration with the same internal structure and with a different direction is also available without affecting the surroundings. In other words, it is the freedom to choose an axis. Moreover, there is another freedom of the rotation around the axis. Both are the case now. The inside of each triacontahedral cages can be treated independently of any other parts. Each of them has 104 different configurations of 9 internal quasi-lattice-points constructing 10 A6's and 9 O6's besides the central O6 which partitions the two cages off. The derivation of the number 104 is given in Appendix B. The missing parts around an edge compose an F20 when the angle is closed. It is mentioned in the last section and Appendix A that F20 and K30 can be constructed only with some A6's and O6's. After all, the number of possible configurations in an expanded rhombohedron is 1042×103 for 89 quasi-lattice-points in the acute case and 103 for 55 quasi-lattice-points in the obtuse case. It
is noted that these numbers should be understood as lower bounds since
there are some other less symmetrical configurations. The counting of the
exact number is rather troublesome and is still an open question. It depends
on the details of the definition of Penrose transformation. Here the author
tried to find the one most highly symmetrical as possible.
5. 3-D Penrose Patterns Starting with any configuration constructed with only A6 and O6, a 3-D Penrose pattern is generated by the infinite time recursive operation of the 3-D Penrose transformation mentioned in the previous section. In each operation in this recursion, the redundant part of the transformation may be chosen arbitrarily. Therefore, the meaning of self-similarity in this case is in a generalized sense. Any way, the composition [A6]/[O6] tends too in the limit of infinite operations, as seen from the former of Eq. (2). The system has a kind of residual entropy due to the multiplicity of the redundancy in the transformation. The structure of the redundancy in the whole recursive transformation is also hierarchic and it brings a geometricseries-like enhanced factor. In the limit of infinitely large system, the value of the residual entropy per quasi-lattice-point is given by S0= [(t2 - ((t9-1)]-1 [(t ln (1642×103) + ln 103] = 0.176 = ln 0.193 (3) In
this respect, a quasicrystal is more closely related with an amorphous
configuration than ever thought on a base of incomplete knowledge on 3-D
Penrose transformation.
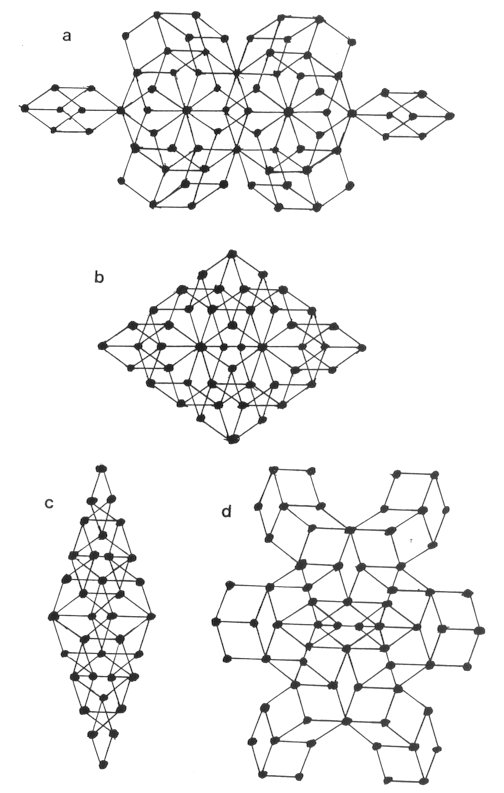
6. Concluding Remarks There are many common features to the projection of the present 3-D pattern (Fig. 2) to some symmetry axes and some experimental results. In the projection along a pentagonal axis, one of the six quasi-basic-vectors is reduced to a point and other five are vectors of length 2t = 0.894 pointing five vertices of a regular pentagon of side length Ö(2(1 - t )) = 1.05 from its center. These fives are the bases of 2-D Penrose pattern. A striking feature of the projection of a skeleton along a pentagonal axis is the presence of regular decagons and its portions surrounded by a ring of regular pentagons. For example, in the case of Fig. 2(b), two overlapping decagons are surrounded with 14 pentagons after four points are properly supplied outside the rhombus. This pentagon in the present case is actually a pentagram in the projection. It means that the concerned five points are not on a plane as the stars in a constellation are not. It is noted that the above mentioned decagon surrounded with pentagons are also regarded as a double ring of decagons.
Fig.
2. The projection of the expanded rhombohedra A6 and O6
along five-fold axes.
Hiraga et al [13] pointed out the similar feature about their high-resolution electron micrograph along a pentagonal axis. The bright dots surrounded by decagonal double ring are distributed all over their image. If one marks such decagons then the marked regions are rather dominant and almost percolated. Figures 2(a) and 2(b), which are the projection of the skeleton of an expanded A6 along two five-fold axes, respectively correspond to Figs. 4(a) and 4(b) of Ref. [13]. Furthermore, the followings should be noted. The smallest decagons in the original version of 2-D Penrose tiling have six quasi-lattice-points in their inside. The same pattern is obtained from the whole configuration of F20 and K30 with all of their inner quasi-lattice-points by projection along a pentagonal axis. Bursill and Lin [14] relates their experimental images to the original version of 2-D Penrose tiling. According to Mackay [15], the self-similarity of linear factor t3 is observed in electron micrograph by Portier et al [16]. As for the composition of Al and Mn in the realized alloys, Kimura et al. concluded to be nearly Al4Mn (~20.5at%Mn) [17]. Compare with Al6Mn (-14.3at%Mn) originally reported by Shechtman et al [1]. Two ideas are proposed for the atomic location by two experimentalist groups; Hiraga et al [18] and Kimura et al [19]. Mn atoms are at the vertices of rhombohedra in both of them. Then each of A6 and O6 contains a manganese atom. The centers of every edges of them are occupied by an aluminum atom. That corresponds to three Al's a rhombohedron. The difference between two assignments concerns the inside of A6. Two Al's according to Hiraga et al. and one according to Kimura et al. are on a principal diagonal of A6. Therefore an A6 corresponds to Al5Mn in the former and to Al4Mn in the latter, while an O6 to Al3Mn in both. After all, two proposed values of the Mn-composition are (2-t)/3= 19.1at%Mn and (4-t)/11=21.7at%Mn respectively by Hiraga et al and Kimura et al. Though the value is open question, such a situation may be referred to as quasistoichiometry in that the composition of the stoichiometric quasi-unit-cells is irrational. The
author is indebted to Professor A.L. Mackay, Professor T. Ninomiya, Professor
S. Hitotsumatsu, Professor K. Miyazaki, Professor S. Takeuchi, Professor
K. Hiraga, Professor M. Hirabayashi, Professor M. Tanemura, Dr. K. Kimura,
Dr. H. Aoki and Mr. K. Senba for valuable discussion.
|