T. Ogawa¹and R. Collins ²

 1 Institute of Applied Physics, University of Tsukuba, Tsukuba 305, Japan, and
   The Institute of Statistical Mathematics, 4-6-7 Minami-Azabu, Minato-ku, Tokyo 106, Japan
   ogawa@bk.tsukuba.ac.jp

 2 Departrnent of Physics, University of York, York Y01 SDD, UK
 

Abstract. The new concept of a graphical geodesic is introduced to characterize an arbitrary two-dimensional network whose meshes are all triangles. Although locally straight, a geodesic line globally meanders and sometimes intersects with itself. Furthermore, it may be open or closed. When the method is applied to the triangulated Penrose tiling, geodesics fall into four classes: chains, flowers, rings and peanuts. The analysis shows that a Penrose tiling has strong local fluctuations of curvature which average out over a small region.

1. Introduction

The Voronoi-Delaunay analysis of a set of point centres in a plane has been applied in many fields of science: the physics of disordered systems, ecology of territories, geographical problems and many others. From this point of view, local data such as number of geometrical neighbours are statistically analyzed. Some related methods for treating more global features are desirable. Such an attempt is made here. Moreover, our method is applicable for any network, not necessarily a Delaunay one.

2. Definition of Graphical Geodesics

Suppose a network whose meshes are all triangles is given. It is shown in Fig. 1 with thin lines with a circle at every knot. Inscribe another triangle determined by the three midpoints of the three edges of every triangular mesh. Then paths are found all over the network which intersect each other at an edge of the mesh. The paths thus obtained are referred to as graphical geodesics. A geodesic line runs locally straight and globally meanders because of local curvatures in the space. Here the local curvature corresponds to the distribution of vertex coordination numbers. In view of this fact, it is useful to define the excess coordination number D_R of vertex R as D_R = z_R - 6 where z_R is the coordination number of vertex R.

For a regular triangular lattice where the coordination number of any vertex is six and their excess coordination numbers are all zero, geodesic lines are three sets of parallel paths. Geodesics tend to converge (diverge) in the presence of a vertex with negative (positive) excess coordination number. If two geodesic lines never intersect, the total excess numbers of all the vertices in the infinite region between them is non-negative.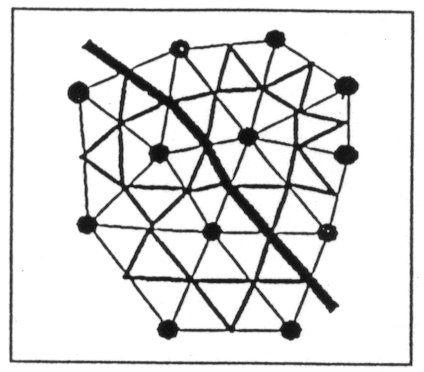

Fig. 1 A triangular network (thin lines with a circle at every knot) and its graphical geodesic
lines (thick lines). A triangle determined by three midpoints of three edges of the mesh of
the network is inscribed. Then the edges of the inscribed triangles form graphical geodesic
lines intersecting at every edge of the meshes. A single geodesic line among them is drawn
as a heavy line.

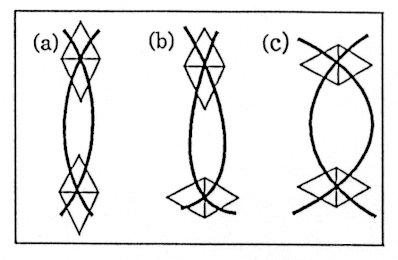
Fig.2 Three types of regions bounded by two geodesic lines. Total excess coordination
numbers in the region are respectively (a) -2, (b) -3, (c) -4.

Two geodesic lines may intersect each other several times. There are three types of closed regions bounded by two geodesic lines. In the first type (Fig.2a), where the angles at both cross points are acute, the total excess coo rdination number in the region is -2. In the second type (Fig.2b), where the angle at one cross point is acute and that.at the other is obtuse, the total excess coordination number in the region is -3. In the third type (Fig.2c), where the angles at both cross points are obtuse, the total excess coordination number in the region is -4.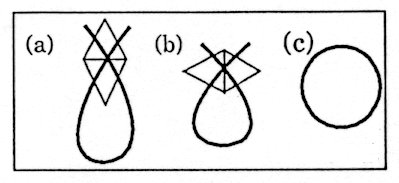

Fig.3 Three types of regions bounded by a single geodesic line. Total excess
coordination number in the region are respectively (a) -4, (b) -5, (c) -6.

There are three types of closed regions bounded by a single curve. In the first type (Fig.3a), where the angle at the cross point is acute, the total excess coordination number in the region is -4. In the second type (Fig.3b), where the angle at the cross point is obtuse, the total excess coordination number in the region is -5. In the third type (Fig. 3c), where a geodesic line closes by itself, the total excess coordination number in the region is -6.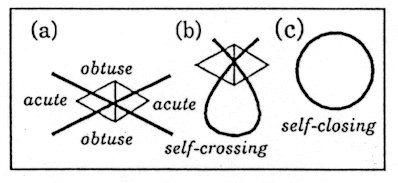

Fig.4 A systematic interpretation of Fig.2 and Fig.3. Regard the region with two
cross points as normal. (a) Assign -1 and -2 respectively to acute and obtuse
angles of a cross point. Assign -3 for each missing cross point.
(b) A self-crossing case. (c) A self-closing case.

These can be systematically interpreted by assigning -1 and -2 respectively to the region of an acute and obtuse portion (respectively not, containing and containing the edge) at a cross point (Fig.4a). Regard the region with two cross points as normal. Assign -3 to every missing cross point; one is missing in a self-crossing case and two are missing in a self-closing case. Add up the two numbers thus assigned. The obtained number is equal to the total excess coordination number of the region.

It is noted that a self-closing geodesic line corresponds to a great circle in the following sense. The total excess coordination number of a triangular polyhedron is -12. The value -6 is half of that.
 

3. Triangulated Penrose Tiling

A triangulated Penrose network is obtained by drawing the minor diagonals of all rhombic tiles (Fig.5(a)). It  is equivalent to the Delaunay network of vertex configuration of rhombic Penrose tiles. The geodesic lines of the triangulated Penrose network are classified into four classes, chains, flowers, rings and peanuts (Fig.5(b)-(d)) and Fig.6, where the diagonals are omitted so that the location in a Penrose tiling might be easily recognized).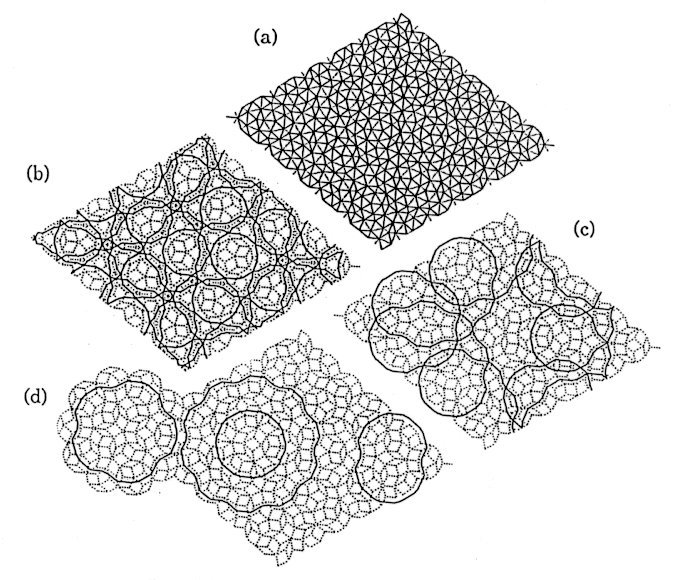

Fig. 5 (a) An example of triangulated Penrose net. All the minor diagonals
are drawn in an acute rhombus of 6th generation. It exactly corresponds to
the Delaunay network of vertex configuration. (b) Ammann lattice constructed
with all chains in the area. (c) Parts of flowers. (d) 60-, 40- (inside) and 80-
(outside) rings and 48-peanut from left to right.

Chains (Fig.5(b)) are macroscopically straight geodesic lines. There are.five sets of parallel geodesic lines. There are only two separation widths for two successive parallel geodesic lines. The ratio of these two is the golden mean. Chains as a whole construct the so-called Ammann lattice. A chain looks like a slalom avoiding S-vertices (using the name by de Bruijn), It never passes an obtuse rhombus parallel to its diagonal. The total excess coordination number is zero in any parallelogram region bounded only by two pairs of parallel chains. Exactly one third of the total length of geodesic lines are chains in the triangulated Penrose tiling.

Rings (Fig.5(d)) are self-closing geodesic lines of nearly circular shape. There are three sizes, of length 40, 60 and 80, where the length is measured as the number of triangles the geodesic line passes through. A 40-ring and an 80-ring enclose a decagon without five-fold symmetry at their centre. The centre of a 60-ring is at a S5 vertex and its inside has perfect five-fold symmetry. 42.75% of the total length of geodesic lines are rings.

The total excess coordination number inside is of course -6, corresponding to a kind of a great circle mentioned at the end of the previous section.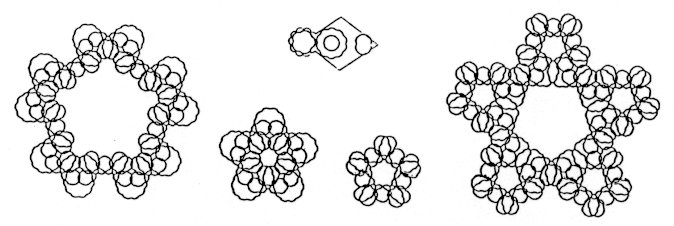

Fig. 6 3180-, 1200-, 780- and 4740-flowers from left to right. There are two systems of flowers:
the one the former two belong to and the other the latter two belong to. A miniature of Fig.5(d)
is shown as a scale of the figure.

Peanuts (Fig.5(d)) are less symmetrical self-closing geodesic lines. There is only one kind of peanut of the length 48. The total excess coordination number inside is also -6. 6.50% of the total length of geodesic lines are peanuts. 

Flowers (Fig.5(c) and Fig.6) are self-crossing and self-closing geodesic lines. They have perfect five-fold symmetry. There are two types: one, with length 165×4ⁿ+540= 1200, 3180, 11100, 42780,..., has its centre at an S5-vertex and the other, with length 330×4ⁿ-540=780, 4740, 20580, 83940,..., has its centre at an S5-vertex. Their varieties are hierarchically infinite. If coarse grained, the edges of higher order flowers are Koch curves of bottom angle 36. 17.41% of the total length of geodesic lines are flowers.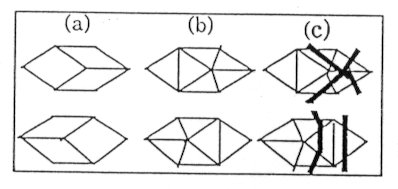

Fig.7 Recombination of geodesic lines. A phason excitation corresponds
to the change between the upper row and the lower. The change in the triangular
network is in (b) and the recombination in (c).

It is noted that a change from a self-crossing geodesic into two self­closing geodesics takes place by rearrangement of three tiles constituting a Q-vertex, which corresponds to the excitation of a phason (see Fig.7). The change is a kind of bifurcation.

From the fact that there are such classes of geodesic lines, some characteristic features of Penrose tiling can be seen. There are strong fluctuations in local curvature, which result in the existence of rings and peanuts. These fluctuations compensate in a narrow region as can be seen from the existence of so many parallel geodesic lines. The self­similarity of Penrose tiling is reflected in the Ammann lattice of chains and hierarchic varieties of flowers. The frequency of vertices with excess coordination number 0 and ±1 is given in Table I, which actually shows rather strong fluctuations of local curvatures. For an irregular network, occurrences of so many pairs of parallel geodesic lines and so many closed geodesic lines can be expected. Existence of flowers must be reflected in some physical properties of Penrose tiling.
 

Table I
Distribution of excess coordination numbers.The names of vertices are due to de Bruijn. The deviation <D²> = 20-12t = 0.58.
 

Note that there are more fluctuations in a self-similar tiling with ten-fold symmetry with -1 £ D £ -4 and <D²>=0.94. The frequency, however, of the strong scatterers with D² > 1 is rather rare. Therefore the geodesic lines go rather straight in wide flat areas and turn suddenly at a strong scatterer. This situation is also seen in the self-similar tiling of octagonal symmetry with squares and 45^o-135^o-rhombi (-1  £  D  £  2 and <D²> = 1.03). In these cases, there is a ring geodesic at every strong scatterer since the excess coordination number at the n-fold centre is n-6 and that of then neighbours is -1 (when n³8): (n-6)+n×(-1) = -6. It is noted that the area of averaging out is wide in these tilings with a large deflation ratio. One cannot help noticing how high the uniformity of the original Penrose tiling is.