


: Fibonacci like sequences made
: pascal like triangles
: Sierpinski like gaskets made
Contents
Here we are going to see many pictures made from these Pascal like triangles.
Some of the authors (Nakagawa, Yamauchi, S.Hashiba and Matsui) spent much time to make beautiful pictures.
In Example 2 and 3 we can see Sierpinski like triangles of numbers made from Pascal like triangle.
In Example 4 we can see Sierpinski like gaskets made from Pascal like triangles by substituting numbers with colored dots..
The similarities and differences of our Sierpinski like gaskets and the original Sierpinski gaskets are very interesting.
In Example 5 we can see beautiful hexagons made from six Sierpinski like gaskets.
Example 2:
Here we use the Pascal like list of numbers {
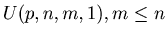 and
and
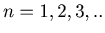 } for
} for
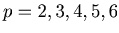 .
If we use the least nonnegative residues of numbers in triangles taken modulo 2, and color them with two colors, then we get the following figures.
.
If we use the least nonnegative residues of numbers in triangles taken modulo 2, and color them with two colors, then we get the following figures.
(1) A Sierpinski like gasket for 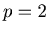 .
Figure(8)
.
Figure(8)
(2) A Sierpinski like gasket for 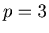 .
Figure(9)
.
Figure(9)
(3) A Sierpinski like gasket for 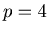 .
Figure(10)
.
Figure(10)
(4) A Sierpinski like gasket for 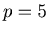 .
Figure(11)
.
Figure(11)
(5) A Sierpinski like gasket for 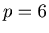 .
Figure(12)
.
Figure(12)
Example 3:
Here we use the Pascal like list of numbers {
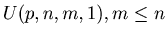 and
and
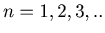 } for
} for
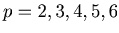 .
If we use the least nonnegative residues of numbers in triangles taken modulo 3, and color them with three colors, then we get the following figures.
.
If we use the least nonnegative residues of numbers in triangles taken modulo 3, and color them with three colors, then we get the following figures.
(1) A Sierpinski like gasket for 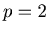 .
Figure(13)
.
Figure(13)
(2) A Sierpinski like gasket for 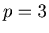 .
Figure(14)
.
Figure(14)
(3) A Sierpinski like gasket for 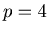 .
Figure(15)
.
Figure(15)
(4) A Sierpinski like gasket for 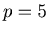 .
Figure(16)
.
Figure(16)
(5) A Sierpinski like gasket for 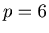 .
Figure(17)
.
Figure(17)
Example 4:
Here we use the Pascal like list of numbers {
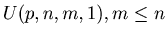 and
and
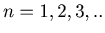 } for
} for
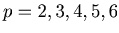 .
If we use the least nonnegative residues of numbers in triangles taken modulo 2, and substitute them with dots of two different colors, then we get the following figures.
.
If we use the least nonnegative residues of numbers in triangles taken modulo 2, and substitute them with dots of two different colors, then we get the following figures.
(1) A Sierpinski like gasket for 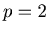 .
Figure(13)
.
Figure(13)
(2) A Sierpinski like gasket for 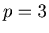 .
Figure(14)
.
Figure(14)
(3) A Sierpinski like gasket for 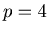 .
Figure(15)
.
Figure(15)
(4) A Sierpinski like gasket for 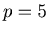 .
Figure(16)
.
Figure(16)
(5) A Sierpinski like gasket for 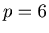 .
Figure(17)
.
Figure(17)
Example 5: Here we can make a hexagon from six Sierpinski like gaskets for
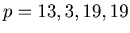 .
Students tried hard to make hexagons beautiful.
The authors made small hexagons, because they had to use high compression rate to make them small enough. Big figures with high compression rate are not good to see.
.
Students tried hard to make hexagons beautiful.
The authors made small hexagons, because they had to use high compression rate to make them small enough. Big figures with high compression rate are not good to see.
(1) A hexagon made from Sierpinski like gaskets for
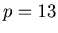 .
.
Figure(18)
(2) A hexagon made from Sierpinski like gaskets for
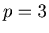 .
Figure(19)
.
Figure(19)
(3) A hexagon made from Sierpinski like gaskets for
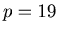 .
Figure(20)
.
Figure(20)
(4) A hexagon made from Sierpinski like gaskets for
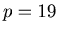 .
Figure(21)
.
Figure(21)



: Fibonacci like sequences made
: pascal like triangles
: Sierpinski like gaskets made
Contents
![\includegraphics[height=10cm,clip]{sierpinski1.eps}](img91.gif)
![\includegraphics[height=10cm,clip]{sierpinski1.eps}](img91.gif)
![\includegraphics[height=10cm,clip]{sierpinski2.eps}](img92.gif)
![\includegraphics[height=10cm,clip]{sierpinski3.eps}](img94.gif)
![\includegraphics[height=10cm,clip]{sierpinski4.eps}](img96.gif)
![\includegraphics[height=10cm,clip]{sierpinski5.eps}](img98.gif)
![\includegraphics[height=12cm,clip]{sierpinski3-1.eps}](img99.gif)
![\includegraphics[height=12cm,clip]{sierpinski3-2.eps}](img100.gif)
![\includegraphics[height=12cm,clip]{sierpinski3-3.eps}](img101.gif)
![\includegraphics[height=12cm,clip]{sierpinski3-4.eps}](img102.gif)
![\includegraphics[height=12cm,clip]{sierpinski3-5.eps}](img103.gif)
![\includegraphics[height=10cm,clip]{sierpinskib-1.eps}](img104.gif)
![\includegraphics[height=10cm,clip]{sierpinskib-2.eps}](img105.gif)
![\includegraphics[height=10cm,clip]{sierpinskib-3.eps}](img106.gif)
![\includegraphics[height=10cm,clip]{sierpinskib-4.eps}](img107.gif)
![\includegraphics[height=10cm,clip]{sierpinskib-5.eps}](img108.gif)
![]() .
Students tried hard to make hexagons beautiful.
The authors made small hexagons, because they had to use high compression rate to make them small enough. Big figures with high compression rate are not good to see.
.
Students tried hard to make hexagons beautiful.
The authors made small hexagons, because they had to use high compression rate to make them small enough. Big figures with high compression rate are not good to see.![]() .
.
![\includegraphics[height=10cm,clip]{sierpinskibr22.eps}](img111.gif)
![\includegraphics[height=10cm,clip]{sierpinskibr11.eps}](img112.gif)
![\includegraphics[height=10cm,clip]{sierpinskiyr23.eps}](img114.gif)
![\includegraphics[height=10cm,clip]{sierpinskiyr22.eps}](img115.gif)