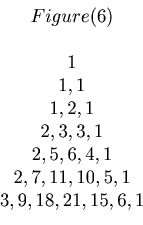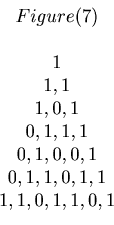


: A gallery of beautiful
: pascal like triangles
: The mathematical background for
Contents
The fractions
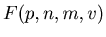 have many interesting properties, but here we are going to study
have many interesting properties, but here we are going to study
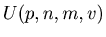 .
See the following Figure 5 and 6.
.
See the following Figure 5 and 6.
We let 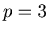 and
and 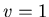 , and make a triangle by
, and make a triangle by
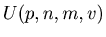 for natural numbers
for natural numbers 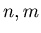 with
with 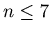 and
and 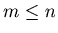 .
Then we get the following Figure 5.
.
Then we get the following Figure 5.
If we calculate each
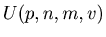 , then we get the following Figure 6.
, then we get the following Figure 6.
One of the authors (Matsui) studied the least nonnegative residues of numbers in Figure 6 taken modulo 2, and he got the following Figure 7. He is a freshman in a high school, and he did not know the Sierpinski Gasket. Therefore his discovery shows an amazing possibility of young students.
After he discovered Figure 7, he colored 1,0 with different colours. In the next section you can see many beautiful pictures made from these Pascal like triangles.



: A gallery of beautiful
: pascal like triangles
: The mathematical background for
Contents