Algorithm B.
1. Take the
continued
fraction expansion of x. Cut the sequence {ak}
up to the (m+1)-th term to obtain a0 ,
a1, ...,
am;
2. Create a
sequence of pairs {(ak, am-k),
k = 0, 1,..., m};
3. Rotate each
point Ak = (ak, am-k) counterclockwise
about the origin, and draw this part of polygonal line
g(x,
m) = A0A1...Am.
The graph
g(x,
m) is obviously a symmetric figure with respect to the
y-axis, the reason to call it
symmetrogram of x. It can
be used as another "portrait" of this number. Also, as we will see, the
shape of
g(x,
m) heavily depends on m.
Like in the previous section, we
will supply some examples. Note that the numbers with the greater diverse
in
the sequence {ak}
will have more interesting symmetrograms than these with finite or uniform
expansions.
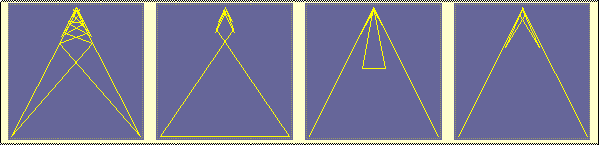
Let us start with numbers containing
p: The figure below shows
symmetrograms g(p,
31),
g(p2,
12),
g(Öp,18)
and g(1/p,25).
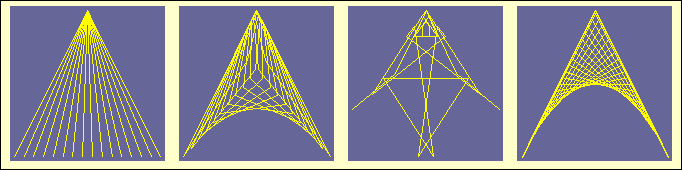
E-numbers are peculiar as in the case of Brownian walk graphs. Here we
display the sequence g(e,50),
g(e2,65),
g(e3,30)
and g(e1/4,70)
(figure below).
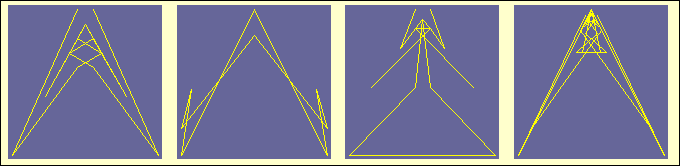
The first two subpictures of the next figure represents g(Log
(2),
17), g(Log
(3),
9). Next two subfigures show
the dependence of a symmetrogram
on m - the length of the sequence {ak}.
These contains the graphs g(g,
18)
and g(g,32)
(g »
0.577216..., the Euler gamma).
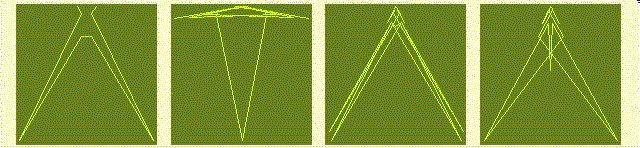
The next row shows symmetrograms of numbers obtained by the Bessel function
of the first kind, Jn(x), i.e.
g(J4(2.1),26),
g(J4(8),12),
g(J2(9),12)
and g(J4(e),39).

Symmetrograms, obtained by Algorithm B are also numerically very sensitive.
This will be confirmed by
the leftmost two subframes of the next figure that represents numbers
cos (1) and cos (1+ 10-10) for the
same m = 27. The rightmost subframes are portraits of
sin(1)
(8 points) and sin2(1) (39 points).
The following four figures show g(Arcsin
(1),
12) , g(sh(sin
(1)),
20) , g(ch(sh
(1)),
12) and g(ch(sin
(1)),
23),
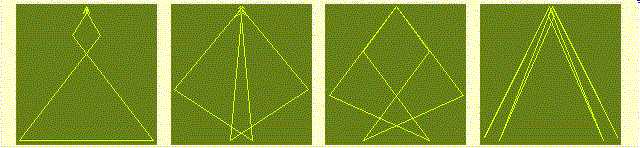
while the hyperbolic functions produce the symmetrograms g
(sh(1),12),
g(ch(1),15),
g(sh(1),15),
and
g(sh(0.35),17)
shown on the figure below.
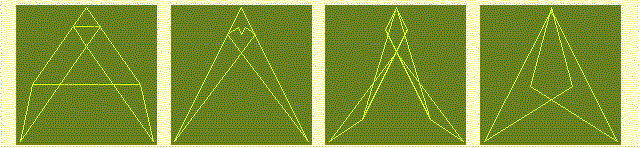
NEXT
VisMath Home