The Soft Logic of Thomas Harriot
H. T. Goranson, Sirius-Beta
Abstract
Until recently, First Order Logic has suffered from an inadequate representation of the situation. This has imposed significant limitations in real-world modeling. We see that an early innovator in logic had this concept but it was dropped by successors because of notational complexity. We present a likely introspective notation of the early scholar, Harriot; we outline the Hermetic influence on this idea (of introspection); and provide a newly discovered interesting influence from the New World.
Introduction
The historical sequence of how mathematical ideas unfolded is almost never the best logical development for my own understanding. But sometimes the historic evolution itself provides significant insight into ideas. And sometimes parts of ideas are lost as they pass from one thinker to another.
Such is the case with a recent problem in logic that I have encountered. In particular, an inadequacy in ordinary logic can be traced to the algebraic system Thomas Harriot imperfectly supplied to René Descartes, and this inadequacy limits the ability to do "soft" modeling, which we define below. Working the other way, insights from logic provide some new interpretation of a specific important artifact from this period. Finally, the identified inadequacy in logic has been addressed in the last decade by some elegant techniques which history validates.
The Problem
My own work is in logic-based modeling of collaborative enterprises [1]. There is a long tradition of such representations in the industrial engineering community; in the past decade, such representations have been extended to all elements of the business enterprise for all sorts of valuable tasks. Enterprise integration, business process re-engineering and simulation are among the most common. The economic benefits of this application of logic are very strong, and the area is booming. Unfortunately, there are problems.
The simplest problem is that most modeling methods are not rigorously formal— but only if they are can we perform meaningful analyses. So the logical basis of such models has become a matter of some study. Some researchers in the community are working under leadership of the U. S. National Institute of Standards and Technology to create an axiomatically formal basis for such knowledge representation [2]. So already, it is possible to have a mathematically rigorous representation of a small domain in a complex enterprise.
But in the general case, there are many situations in which First Order Logic (FOL) encounters difficulties. One of these is the completeness problem: in order to perform system-level analyses (the usual case), one must model some critical mass of the enterprise. There is no formal place-holder for yet-unmodeled phenomena. Since the really interesting enterprises are of the size of, say, Boeing, the requirement for complete modeling becomes unrealistically expensive.
More substantial problems exist, though. FOL can be used in cases where behavior is governed by the so-called hard sciences, physics, chemistry, biology and the like. In this case, causal behavior can always be reduced to basic well-founded primitives. But many processes in the world fall into the "soft" sciences. In this case, the behavior below a certain level of granularity cannot be well described. For instance, how well a certain person will collaborate in an organization defies all by the most general of formal descriptions. Unfortunately a great many problems in business, medicine and economics are of this type, and many bad decisions are made as a result.
So we cannot effectively model cultural and social phenomenon, nor the phenomena that we cannot afford to. But there is an even more vexing problem, modeling the future which is full of not only simple uncertainty, but unexpected "types" of certainty. There are many cases where we have great capability to answer questions, but simply don't know what the right question is.
These three types define the soft modeling problem: context that is unknown, entities which are known but whose behavior is not fully explicable, and entities whose behavior can be well explicated but is not for some reason such as cost or some other logistic barrier.
Workshops [3] on the soft problems fault not only the lack of care in modeling, but more fundamentally the inability of logic itself to provide a basis for soft problems.
Thomas Harriot (1560-1621) is the hero of our story, though an unsung hero in general knowledge. We know little of this English scientist because of the peculiarity that great thinkers are known through their books, and Harriot wrote essentially none. His environment was such that he was constantly under threat of trial for heresy by the English courts. And in fact, his sponsors were imprisoned and in some cases beheaded for notions almost certainly guided by Harriot. We know that he went through several periods where he destroyed every important record just before a trial. In a letter to Galileo, he congratulated his fellow scientist on his courage in publishing and complained that he couldn't do so. When Galileo did publish, he suffered as a result of course. Probably what Harriot had most in mind was the fate of his colleague, Giordano Bruno, who was burned as a heretic in Rome in 1600.
Until recently it was thought that the few of Harriot's writings that survived perished in the great fire of London in 1666. But in the 1980's some of his notes were found in the home of his primary sponsor, the so-called "Wizard" Earl of Northumberland. This very wealthy patron was obsessed with Harriot's work and devoted much of his time and treasury to it. So integrated into the house was Harriot that he acted as stewart of the household accounts for decades and was effectively the master while the Earl was imprisoned for many years. Interestingly, during the Earl's lengthy imprisonment in the Tower, he was able to receive visitors. He and co-prisoner Walter Raleigh (who was Harriot's other patron) were able to set up an alchemical laboratory in the Tower and conduct experiments under Harriot's guidance. And they apparently hosted a scientific salon.
At any rate, this blending of roles, and the mixing of scientific with surviving household papers, has provided a glimpse of Harriot's achievement, and his reputation is beginning to be repaired. He invented the radical sign and popularized the equals signs and the form of expressing equations (left side/right side) which is second nature today. He was a major figure in optics: built the first telescope in England, and there are indications he provided key technology to the Dutch innovators to create the first ones overall. We know now that he made the first map of the Moon and was the real first discoverer of Jupiter's moons.
To aid Raleigh and the Queen in their sea ventures, he greatly advanced spherical trigonometry and devised new navigation instruments as well as beginning a science of dynamic stability to aid in seavessel design. He investigated the optimum packing of cannonballs: his conjecture, conveyed to Kepler and known by the latter's name was only recently proved [4]. He was also an active innovator in linguistics, chemistry and even accounting methods. We won't review everything here; what is cogent is that in lieue of publishing, he shared his results in correspondence, often clandestine, with his peers. What concerns us here is his work on the algebra of concepts. This was used by Descartes as his primary formal foundation for his new system of logic.
The Logical Kabbalah
A conventional history of logic before Descartes has settled into a comfortable litany of steps consisting of the Greek schools colored over time by the medieval Church. From our modern perspective, we are careful to distinguish "real" science from the occult, pseudoscience and other silliness. So we project that distinction back into history. Actually, things were not so clean: until around 1600, the study of science was as likely to involve mystical traditions as not. And such was the case with logic, and the thread of the history of logic through hermetic Kabbalah.
Kabbalah is difficult to describe briefly, because it has such a long history and has been coopted for many special interests. It is primarily the Jewish mystical tradition, allegedly the component of God's wisdom to Moses that, by virtue of its transcendence, could only conveyed orally. It is possibly quite older than Judaism, as it probably has Zoroastrian origins; some ideas are suspected to have been inserted in Jewish tradition with Darius' rebuilding of the Temple a half-millenium before Christ. It is notable that the original Zoroastrian tradition was largely concerned with the representation of the divine; in order to get closer to the divine, one had to have representations which do not unduly debase. The idea of an ordered grammar itself can be seen in the related orderliness of sanscrit.
Kabbalah in the Jewish tradition originally focused on the representation of the literal Hebrew scriptures, and dealt with such issues as the shape and semiotic meaning of the letters themselves; how combinations of these can form representations which have meanings on different, "hidden" planes; and on the internal logics conveyed by representation composed by phrases and chapters. In other words, Kabbalah was the study of abstraction, albeit in the context of the representation of divine wisdom.
How strong this tradition was before about 1000 CE can only be inferred indirectly because if it existed, it was an oral tradition. But after the millenium, especially in Spain, study greatly increased and books started to appear. While very mystically oriented and tightly linked to by-then very codified Jewish thought, Kabbalistic writings stuck to the agenda of defining abstraction. After several iterations, a specific structure emerged to describe the cosmos and all its principles. This is a geometric figure of circles and lines with compex symmetry, the so-called "Tree of Life" which we'll describe in a moment. It can be said that all Kabbalah is considered to be coded in the Tree.
During this time, basic philosphical battles were raging within Christianity with the dominating views claiming both divine guidance and ancient provenace. One of these groups, influenced by neo-Platonists, coopted Kabbalah, specifically the Tree, and incorporated it in a document purportedly written in most ancient times by the Egyptian adept, Hermes Trismegestes. Thus, a separate branch of Kabbalah was spawned. While Jewish Kabbalah remained relatively static, Hermetic Kabbalah became a versatile, dynamic basis for much of what we would term scientific and mathematical speculation. That the Tree specifically addressed a number theory as well as a causal abstraction chain helped. Each Hebrew letter also stands for a number, so while letter combinations convey semantic meaning, their numerical equivalents carried an additional numerological semantics, thought to suppliment the exoteric one.
Thus, one can trace a second root of the history of logic, bumping against the Greek root, both supplimenting and competing with it. It is this root which was the source of the richest of ideas, if only because the alternative was innately constrained by religious conservatism. Many late 16th-century scientists/alchemists were Kabbalists in some sense, and this was the case with our Thomas Harriot.
He sat on the cusp of modern science. On one side were his mentors John Dee (who recorded conversations with angels) and the philosopher/magician Giordano Bruno. On the other side were experimentalists Kepler, Galileo, Descartes and later Newton. Harriot influenced the theory of inductive reasoning reported by Francis Bacon, but at the same time influenced Kepler's 1596 theory of matching planetary orbits to "vibrations" of regular polytopes. This seems comical to us today—just a stupid error— as we've lost some of the historical perspective
After 1620, Hermetic Kabbalism spawned a new breed of occult society: secret Rosicrucianism and such which chose to ignore the emerging scientific thought. As occultism and science diverged, Kabbalah, the Tree and its cousin, Tarot cards, went through a modern reinvention into realms of silliness and quackery. As a result, we retrospectively tend to dismiss the influence of the hermetic ideas on someone like Harriot.
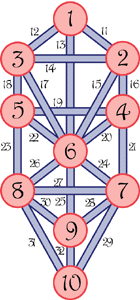
The Tree of Life is shown in Figure 1. It consists of 10 circles connected by 22 lines, and has several internal structures. For instance, the circles are numbered. Number 10 is the physical world in which we live. It "emanates" from a set of higher abstractions denoted by Circle 9. 9 is the emanation of 8 on up until the metalevels become so basic and pure that the last is the "nothing beyond nothing."
[Figure 1, The Tree of Life, with Simple Structures (click each for larger)]
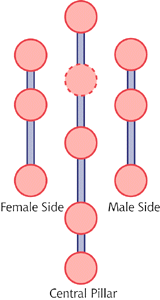
Another structure is the three pillars on the left, right and center. The emanations are only made possible through the differences between left and right which incorporate all dualisms (male/female, light/dark, cold/hot and so on). Circles on the center are a special kind of synthesis of the two sides in that while balanced, they contain left/right forces in an especially potent mix.
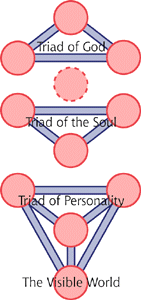
The basic unit of the world above #10 is the triad of one right, left and center circle; there are three of these, each with an internal balance and self-contained engine of abstraction. Each of the lower triads is an emanation of the abstracted one above it in much in the same way as the circles.
Finally, consider the lines. Each of the circles has semantic association in every category: birds, emotions, colors and so on. And each of the lines has a distinct semantics which represents the relationship between the two. It's quite a sophisticated concept this, that each line—meaning each relationship—is a first class entity in the conceptual system. Each of these lines has somewhat more power in the Tree cosmology than the circles. We might call them functions and that's the way the Kabbalists of both stripes felt. (Each of these 22 paths define a letter of the Hebrew alphabet. The idea of the the word as directly synthesized from basic cosmic forces is a critical foundation for "the religion of the book.")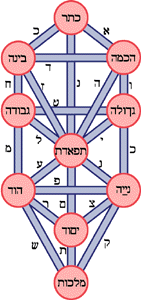
[Figure 2, The Hebrew Letters (click for larger)]
During Harriot's time there was quite the controversy over the role of the divine, specifically Jesus, in any system of abstraction. In particular, the early Hermetic Tree assigned circle #6 to Jesus. For reasons not of interest here, dogma held it impossible to have such a system without Christ at the "center." A more modern view held that any wise person, later called an adept, could stand for that role. (This in fact could stand as the definition of modernity.) In was in this context that Harriot led an expedition to the New World in 1584 for Walter Raleigh.
Others on the voyage were tasked with the search for gold and such. The metallurgist selected by Harriot for the voyage was himself a Kabbalist, Joachim Ganz. We know this because his father, David Gans was a well known astronomer and historian who studied with the Kabbalists of Prague. The younger Gans alchemical workshop of 1584 was recently discovered in North Carolina [5].
Harriot's charter on this voyage was evolved from Raleigh's "School of Night" which explored hermetic/scientific ideas in a Protestant context; Harriot was to search for New World wisdom to revolutionize thought. (Politically, Raleigh's enterprise, later to be the Virginia Company was opposed by the neo-Hebrew Puritans who supported the Levant Company to seek a revival of Christ-centered science in the Holy Land.) Accordingly, a destination in modern Virginia was chosen as it was a reputed center of Indian priests, thought to be a rich source of ancient wisdom, perhaps even from Lost Tribes of Israel. A native American from this area had been supplied to Harriot beforehand, and he had made a thorough study of the language. (His linguistically sophisticated phonetic alphabet survives and is used in the example.)
While others went off prospecting, he in fact spent the winter of 1584-5 with this tribe of Native Americans. On his return to England, we infer that he reported an existence proof of a Kabbalah (and therefore a system of logical abstraction) without Christ. Native Americans had never even heard of Jesus, yet had—he thought—recreated the Tree of Life. I have recognized the Tree in a key artifact from this period. The chief Indian priest's robe found its way to England as a gift to King James in 1608. Shakespeare's The Tempest portrays Harriot as a Magus who employs a magic robe which almost certainly refers to this. It is now in tha Ashmolian in Oxford. Figure 3 shows a photograph of the robe, a rather luxurious item in terms of labor.
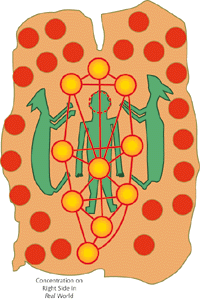
[Figure 3, The Mantle (click for larger)]
To the right of this photograph, we've drawn the features of this robe. (The lines have been added for clarity.) Notice the ten circles of the Tree of Life. The man imposed on the diagram has his head located where an eleventh, "invisible" circle is placed, which makes the European-American correspondence even more remarkable. Arrayed around the Tree are 22 disks representing the 22 lines. The two upward-looking hares are representative of spirits that help the local deity.
(In fact many stylistic peculiarities of this diagram (not discussed here) are so similar to European models that it is unlikely to have been of aboriginal derivation, and there is a potential early European contact which could account for it.)
But Harriot thought it a spontaneous parallel discovery from the New World, we think, and this stimulated thinking about a religion-free system of abstraction and logic. No wonder Harriot was concerned about heresy trials!
The Situation in Logic: Kabbalah
That story is interesting in a general context of the history of science. But there are lessons for logic as well. Consider the basic hermetic unit, the triad. Key components here are two circles on the left and right, two collections of information if you will. Connecting them is a horizontal line representing a relation between them. This is a simple graphical notation for a functional logic.
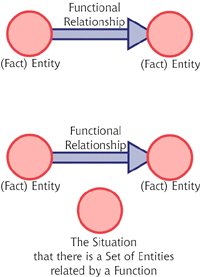[Figure 4, the Kabbalistic Situation (click for larger)]
What's notable is the third circle below, which represents the "situation" that exists of the two pieces of information and their relationship (or if you like, the function that transforms one to another.) So, in this system we have three distinct notions: facts, functions among facts, and the situation that there are facts that are functionally related.
We can only infer how Harriot handled these three notions so that they are all first class entities in his system of logic. Fortunately, we have work of his contemporaries. The facts were conveyed by symbolic variables as they are today. The relating functions were expressed by the form of equations as they are today. While Harriot didn't invent this by any means, he cleaned it up and standardized it.
The situational semantics, expression of the third entity, was conveyed by shapes of the letters of the variables. These together formed "words" that had a parallel meaning in the equation sort of "on top" after the manner of Kabbalistic scripture: the words had a meaning from their speech-derived semantics, and also a parallel "situational" one from their numerologically-derived semantics.
The system of Gematria, the extraction of a second meaning from the numerical value of Hebrew letters, has many systems. The most primitive calculate a single number from each word and link that number to some special meaning. More complex systems keep the number for each word distinct and interpret the number stream in terms of recurring patterns, much as music. The most complex systems translate the numbers into letters and words again, so that each phrase contains its own commentary.
Such a system was employed by John Dee, England's senior scientist of the generation just before Harriot. The trick for Kabbalists of the day was to devise an alphabet that could communicate phonetic and annotative meaning in the same words. In Dee's case, this was what he called the Enochian Alphabet. Like many from this period, it is unsophisticated in that Enochian letters correspond roughly to Roman letters, but rather interesting in that he means to inherit from the Hebrew the vast symbology by linking each letter to one of the functional links on the Tree of Life. Each character has a plant, color, emotion, planet and so one associated with it. In this way, a written phrase conveys a whole scene on its metalevel. But gleaning the "proper" meaning from his letters alone would be quite impossible. There is nothing like a well-formed ontology and an ordinary reader would be excluded from the annotative meaning.
Harriot's alphabet was more sophisticated in that it denotes phonemes, likely the first systematic approach to grouping sounds by the geometry of the mouth and tongue. Each character physically is drawn from a combination of paths from the Tree.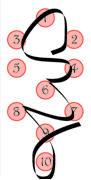 
Harriot's combining of paths and "circles" in a single character allowed him to make more concise statements. For him, the meaning was in the functional transforms that related a set of circles. In other words, each character was a notation of a collection of functions in itself. By wisely choosing the characters he used in equations (as we do today), he could convey not only the statement of the equation, but also a collection of metastatements that convey the general situation of the equation. Moreover, both meanings had the additional property of being (with some unknown algebraic shorthand) pronouncable as a phrase.
But this is still unduly cumbersome notation, quite beyond the assumption that someone can parse the cosmological primitives of the Kabbalistic cosmology in the Tree. No wonder Descartes eschewed it in adopting only the superficial notation. (Descartes may not have been completely conscious in this. The published explication of Harriot's algebra, in 1631, by a student who deliberately expunged much of what he considered heretical. Harriot died ten years earlier; Descartes great work appeared in 1637.)
This is an example of a case where a poor notational system was so cumbersome that it prevented mathematicians from dealing with a central concept. As it happens, Descartes focused on the first two concepts because they were well developed in the Greek tradition and because Harriot's algebra made them easier while making the third unpalatable. As a result, we've evolved a system of logic that is biased in certain ways and is poorly suited for many exercises in rationalism.
This inadequacy was a significant part of what fueled the "alternative" of rosicrucianism and such and continues to be the engine which makes antiscientific new-agism attractive to people today. The first formal statement of the inadequacy was Peirce's 1852 study of pragmatics [6] which stated that a "thirdness" was essential to a well-founded system of logic, an element missing in the logic of his time. For the next hundred years, pragmatics were dealt with in inelegant ways, lacking elevation as a well-founded integrated part of the mathematics. While Boole went off in a thread resulting in remarkable utility, contemporary logician Charles Dodgson emphasized all the humorous inadequacies of the current system. Interestingly, Dodgson (best known as Lewis Carroll of the "Alice in Wonderland" books) was a student of both hermeticism and Harriot. The former was through his associations with various occult societies, the latter in his role as librarian at Oxford.
(There is much to say about the Carroll/Harriot Kabbalah link which is being prepared in forthcoming book.)
Just because a renaissance scientist believes something doesn't make it so. But it does seem to be the case that Harriot's situation was like the button: Romans used them extensively. Then the button became forgotten with the collapse of the empire and in particular, loss of button infrastructure. In that case, it was a thousand years before the button reemerged.
It wasn't until the 1980s that "thirdness" was restored to logic. Barwise and Perry [7] introduced the notion of a "situation" as a first class object in logic. A situation is a simple entity which can carry context and attitude. Thus, reasoning about anything interesting can now deal with reasoning over soft objects as well.
The power of a situation is that it can act as a placeholder for information which is necessary to the analysis, but which for some reason is not expressible as facts. What's interesting is how this problem was solved. Harriot expressed situational information distributed in the context of the situation of the equation. This makes sense, that there should be a mapping from the role contextual appearance plays in the real world to the role it plays in the equation representing it. But the vagueness in the content of the situation conveyed to vagusness in the notation. And above all the notation must be unambiguous. Situation Theory has not yet been extended to the most difficult of soft objects, but it does seem capable of doing so.
Harriot's technique was to add metameaning within each variable and their combinations. The modern, less notationally cumbersome solution is to create a discrete notational class of object and to create a new type of relation within the equation. This reproduces the hermetic notion that had both facts (left and right circles) and situations (the central circle) as the same "type" of object.
It seems that insights often outrun the mechanics used to manage them, and both are restricted when the notation is inappropriate. It seems that logic could have developed as a more capable soft logic, more widely applicable. Instead, it lost its ability around 1600 because of inelegant notation. It's been reinstated now not only because we have the insights, and the formal mechanics, but also because of innovation in the notation. We may now have the foundations of a new soft logic [8] that was dropped from the agenda.
I am indebted to Lee Bloomquist and Keith Devlin who introduced me to Situation Theory, to Stephen Goranson who corrected some history of Kabbalah, and to John Collier who pointed me to Peirce's thirdness.
References
1. Goranson, H. T.: The Agile Virtual Enterprise, Quorum, Westport Conn, 1999.
2. For information on the Process Specification Language: http://www.mel.nist.gov/psl
3. Goranson, H. T.: The International Conference on Enterprise Integration Modeling Technology in Perspective 1992-1997, in Enterprise Engineering and Integration, Ed K. Kosanke and J. G. Nell Enterprise Engineering and Integration, Springer, Berlin, 1997.
4. Hales, Thomas C.: Sphere Packings I, Discrete and Computational Geometry 17, pp 1-5, 1997.
5. Hume, Ivor Noel: Roanoke Island: America's First Science Center, in Colonial Williamsburg 16.3 (Spring 1994), pp 14-28.
6. Peirce, C. S.: Collected Papers, ed Charles Hartshorne and Paul Weiss, Cambridge University Press, Cambridge, 1960.
7. Barwise, Jon and John Perry: Situations and Attitudes, MIT Press, Cambridge Mass, 1983.
8. Devlin, Keith: Goodbye Descartes: the End of Logic and the Search for the New Cosmology of Mind, John Wiley and Sons, New York, 1997.
9. Shirley, John W. Thomas Harriot: a Biography, Oxford University Press, 1983.