|
(4) Differences in views of the same size There are two shapes of the same size. These are examples for a kind of illusion to recognize that these shapes with the same size look different due to a slight difference in the backgrounds.
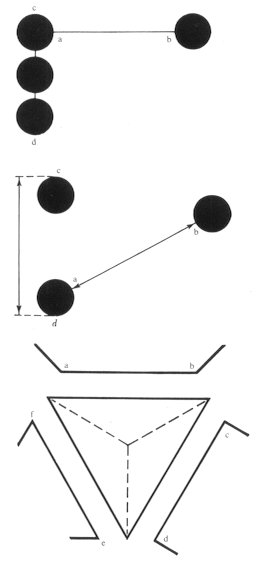
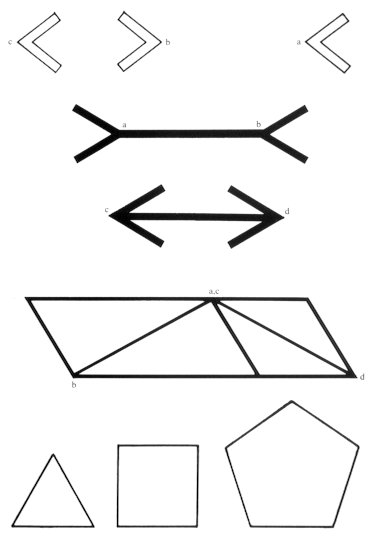
(i) Illusion of length Let's analyze the famous Muller Lyer's illusion (Fig. 327). The distances of the points with a finite size drawn in Figures 323 and 324 look different. This is because we tend to determine the distance between the points as that between the centers of the points when we measure a distance between these points with our eyes. This is the same in the case where a carpenter measures between the centers (center-center) of pillars. And, we feel that the distance of cd is shorter than that of ab since the points a, b, c, and d tend to be pulled toward the centers of the circle (point shape). The illusion in Figure 326 is based on a similar principle regarding the bending shapes as a point shape. If the above are understood, the illusion in Figure 327 by Muller Lyer has been almost solved.
·
Figures 325, 328, and 329 belong to a different category of the illusion diagrams from the above.
It depends on whether these lines being investigated belong to larger shapes or smaller shapes. In
other words, it tends to be seen that a straight line which belongs to a larger shape looks longer than
that which belongs to a smaller shape.
|