|
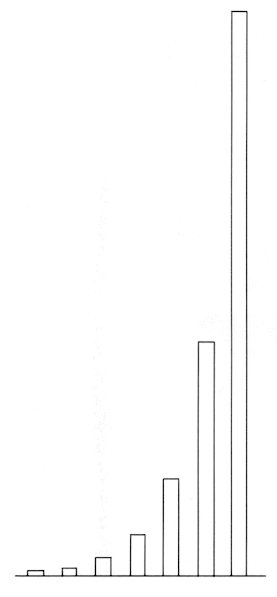
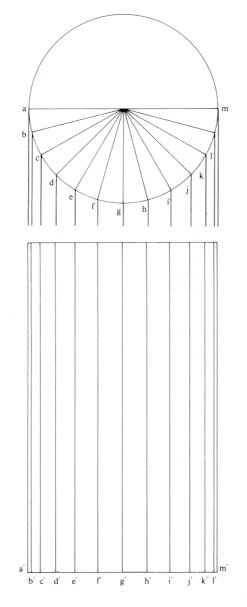
· Progressions with a structure of the harmonic oscillation Normal projections of the equally dividing points on a perimeter of a circle are shown in Figure 256-a. These exactly represent the structure of the harmonic oscillation. Using a progression of the points with this structure, a bundle of the parallel lines with the same length, is drawn. This makes a diagram which has a similar feeling of a cylinder and a round surface (Fig. 256-b). This is the same as the view of the parallel lines drawn on a cylindrical surface with an equal interval seen from just in front.
· Progression created by oneself
Figure 252 on the preceding page is the arrays of intersecting points of the perimeters of the
circles of the equal radius, and the centers are aligned in the same distance on a straight line.
When we pick up any point which is located in a vertical line, this is also supposed to be a
progression, too. Only, we don't know the formula which represents it. Figure 254 is an equal area
division of a circle. In other words, all the areas surrounded by neighboring circles are equal. The
interval of the spacing between circles also forms a progression created by such a condition or a
structure.
|