|
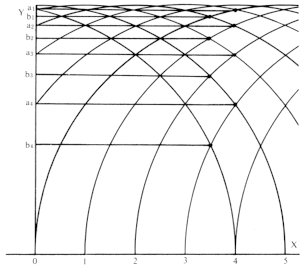
(v) Other progressions There are progressions which are led from clear formulas. Though we do not know what kind of expression the formula will be, some are easily obtained geometrically in drawing. As the former example, there are an arithmetic progression or a harmonic progression, and as the latter example, there is a geometric progressions. The Fibonacci progression has both of the convenience. In order to create good and new shapes that good shapes, either method can be used. The latter method handles shapes from the beginning. Thus, it has an advantage that the work can be continued being ascertained by eyes. The designs belonging to the latter system are mainly selected below (Figs. 252-254).
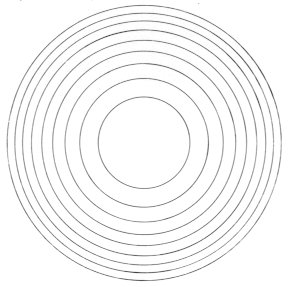
· The progression of Pell The previous term is doubled and added by the second previous term to lead to the next term in the Pell's progression. For example when the first term is 1 and the second term is 2, The third term becomes (2× 2+1) = 5, and the fourth term becomes (5×2+2) = 12, and the following terms are calculated similarly, the progression of 1, 2, 5 12, 29, 70, and so on is obtained. This is a progression of Pell. It is attractive since the numerical value increases rapidly similar to a geometric progression (Fig. 255). Another advantage of this progression is that it
is drawn only using a divider. In other words, a general term is obtained
by doubling the length of the front term and adding the value of the second
previous term to this.
|