|
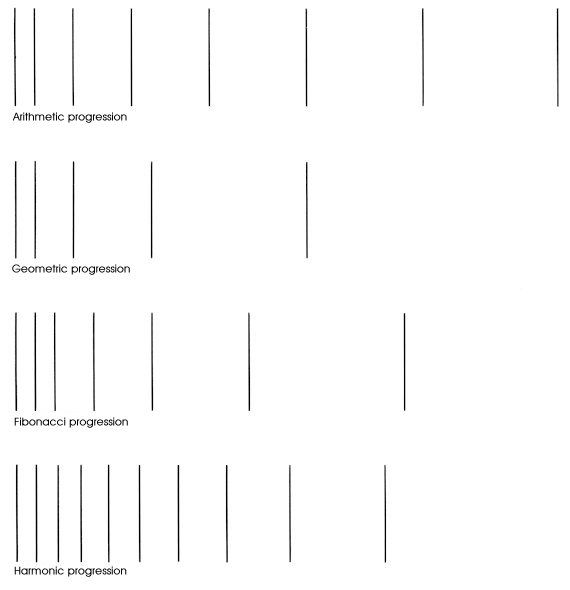
(3) Progression The ratios between two quantities of shapes with a length and an area have been studied a problem up to the previous page. If we treat ratios more than 3, research on progressions are needed. All the groups of numbers generated based on a fixed rule are called progression. These are useful for the arts and designs. However, if the calculations and drawings are not easy, they are actually not suitable for the purpose. Form these view points, the following four typical progressions were selected, and will be investigated their characteristics. (Examples)
The harmonic progression has a form of fraction. Thus, when it is written in the forms of decimals; 1, 0.5, 0.33, 0.25, 0.2, 0.16, 0.14, 0.12, 0.11, 0.1... These can be modified to be more convenient by reversing the orders and multiplied by 10; 1, 1.1, 1.2, 1.4, 1.6, 2, 2.5, 3.3, 5, 10. The four kinds above are drawn in figures and compared as shown below. As for the arithmetic progression, in the progression that a change was fixed a geometric progression increases slowly in the beginning, but it increases rapidly after that. It is a dynamic progression which increases geometrically as the name represents. The Fibonacci progression is rather close to the geometric progression. In the first stage, it does not produce a smooth curve. But later, it increases at a high rate similarly to the geometric progression, which gives us a profile with a speedy feeling (Fig. 241-d).
|
|||