|
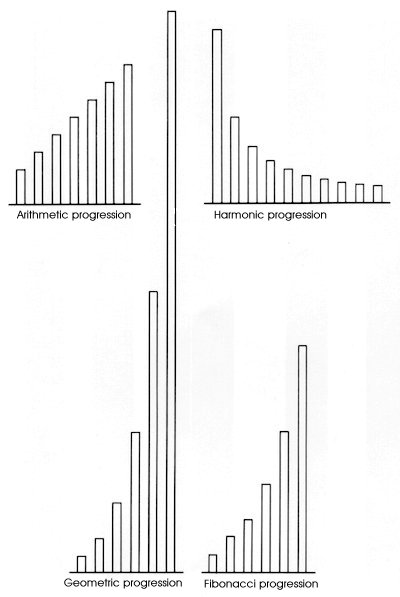
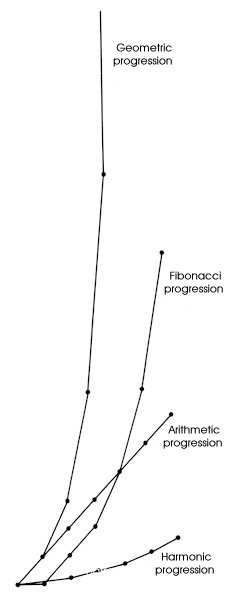
However, the rate of increase isn't so rapid as the geometric progression. It has a gentleness with a rule that a sum of a 2nd previous number and a previous number becomes a next number. When the number n of the n term increases, the ratios between two successive numbers are approaching to the golden ratio. The harmonic progression is made of the reverse of an arithmetic progression, and the number of the term decreases as the term progresses. The ratio of reduction of it is small and the number of the term is approaching toward a constant value. Roughly speaking, it is easy to memorize them if we assume that the geometric progression is similar to a parabola and the harmonic progression is similar to a hyperbola (The arithmetic progression varies linearly). However, these are only the simplification to make us easy to memorize the progressions. If a minus is put to the equation which leads a progression, the profile of the graph will be reversed. By adopting a part of the profiles or modifying variously, a new way of using them differently from the above general characteristics is also possible. We can not limit the way to use them in a fixed way. For example, if an arithmetic progression and a harmonic progression start assuming that their first terms are 1 and the difference is 1 (or the interval of the number of denominator is 1), the second term will be doubled (or 1/2). They show a big increase (decrease) ratio. The variation ratios of the second terms are never said to be small. As a result, the change ratios of the arithmetic progression and the harmonic progression are large if they are partly seen. Therefore, they should be utilized in arts and designs with a good knowledge of them. In the next two pages, several examples of using
the four above-mentioned progressions taken from the works of the practical
studies of two-dimensional KOHSEI (Basic Art & Design).
|
|||||