First, when we examine the number of the ways of arranging two horizontal lines, there are ten kinds because it is a combination for selecting two lines out of the five lines is ₅C₂ (this is the same to the case where two vertical lines are selected). When one vertical and one horizontal line is selected, there are 25 possibilities ( ₅C₁ × ₅C₂ = 25 ). As in the above, the total number will be 45 (10+10+25 = 45) when two lines are used.

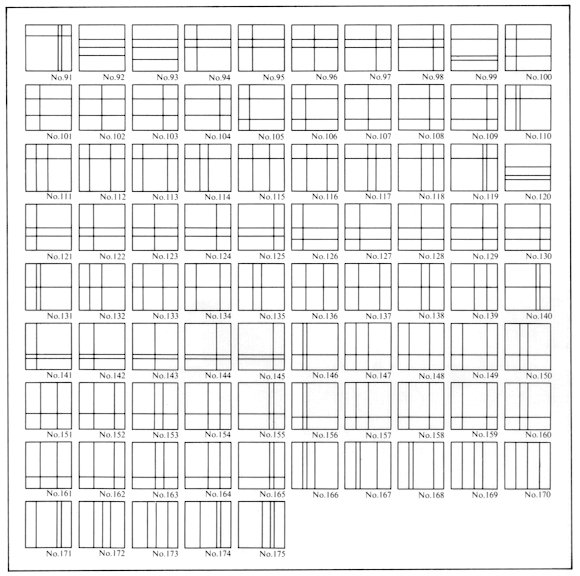
The number of the division using three lines is calculated as follows; three horizontal lines, ₅C₃=10, three vertical lines, ₅C₃=10, two horizontal lines and one vertical line, ₅C₂ × ₅C₂=50, and one horizontal line and two vertical lines, ₅C₁ × ₅C₂=50. The above total number of 120 is the total number of the division using three lines. In the same way, we can sum up the total number by adding these combinations for the case of using four lines one by one. Since all of the resulting numbers are too numerous to supply, only the examples using three dividing lines are illustrated here. We were surprised that so many divisions were made by defining these small dividing points. 
 
 

197-b   Figure 197-a, b: Basic study into the division of a square surface. These figures confirm that there are                                various kinds of phases composed by selecting dividing lines on the bisection, trisection,                               and tetrasection points on the sides of a square. The figures shown on these two pages                                show examples of the divisions using one to three dividing lines. The 175 divisions were                               collected.  (A computer was used).

NEXT

CONTENTS