|
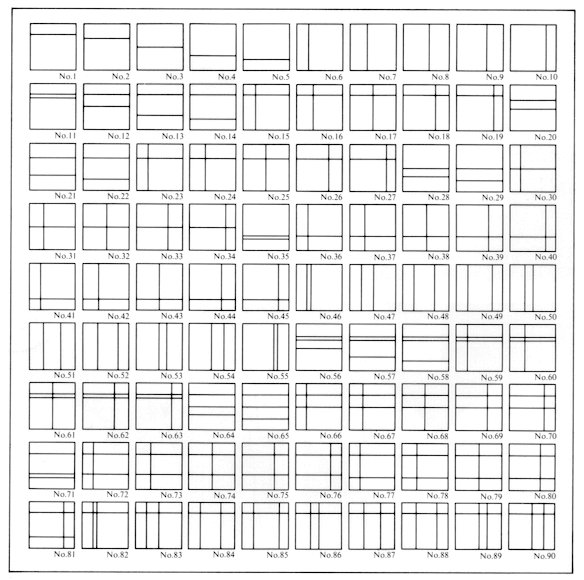
(4) Methods of division and the number of kinds of divisions Figures 197-a, b shown below represent the results of basic research on divisions based on our plan to find methods to divide a square space using bisection points, trisection points, and tetrasection points on the sides of the square. It must be done systematically if we want to find all of them we must examine how many methods there were, respectively, when the number of division lines were increased one by one. If only a dividing line is used, there are five dividing points on each of the vertical and horizontal sides. Thus, there are ten dividing methods. It should be noted here that the figure of No. 1 is equivalent to those of No. 5, No. 6, and No. 10. They are of the same shape and "congruencies" mathematically because they can completely coincide with each other by rotation. However, in the field of art and design, they are not identical even if a line is put upward or downward, because they create a sense of difference. Moreover, drawing a horizontal line or a vertical line will create a larger difference. After all, all four shapes are necessary in the field of art and design, but only one shape is necessary in mathematics. Next, there are three dividing methods using two
lines. They are three possible cases of using two horizontal lines, two
vertical lines, and one horizontal line and one vertical line.
|