|
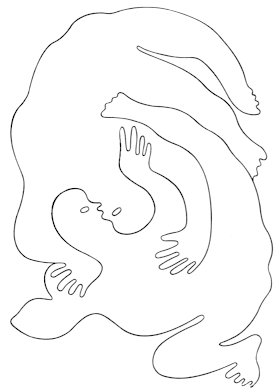
(2) Equal-area division Let's assume that there is a rectangle. When we think of dividing it into two equal shapes, there are various methods. If it is cut on a diagonal, we get two congruent right-angled triangles. Two congruent rectangles are generated if it is cut with a vertical bisection line. Two congruence trapezoids are obtained if it is cut with a straight line passing through the center on any slanted angle. The area of these triangles, rectangles and trapezoids is, respectively, the same though each form is different. Thus, the "equal-area division" theory, that the shapes may be different but the areas must be equal, can be defined. The characteristic of this division is that it generates more variations due to the differences in the shapes than the equal-shaped division. However, because the areas are respectively equal, our eyes are always watching shapes with the same area. This gives us a feeling of equality (the sense of balance and stability) within the area. Yet, it is pretty difficult when we try to do an
equal-area division using concrete configurations, although the picture
of the Escher below is an example that was successful. When areas are measured
strictly, there is a difference of about 10% in the work of Vasarely. However,
sensuously, the two twining figures appear to be of the same size.
|