3.3 The Wallpaper Groups

Definition 3.3.1. A subgroup K of D_E₂ is the wallpaper group if it's translational subgroup is generated by two translations.

A wallpaper group will be denoted by K, it's corresponding translational and point group with T_K and O_K, respectively.

The lattice consists of points ma+nb, m,nÎZ, where translations by independent vectors a and b generate T_K.

From the condition that K is discrete, it follows: there are such a and b, that their module is smaller or equal to the module of any other translation in T_K. In the further exposition, we will consider T_K = áa, bñ, with |a| and |b| as minimal. Depending on the proportion of vectors a and b, we will make the difference between the lattices. The classification of wallpaper groups we begin by the classification of T_K, that is by their lattices. Namely, the lattice will be 'built' of parallelograms (with two exceptions). Regarding the form of 'bricks', the lattice will get it's name.

Without loosing generality, let:

(1) |a|£|b| (otherwise, a « b);

(2) |a-b|£|a+b| (otherwise a ® - b, while because of |b| = |-b|, we have the condition (1) satisfied);

From the conditions (1) and (2) result the possible relations between |a|, |b|, |a-b| and |a+b|:

1) |a| < |b| < |a-b| < |a+b|

- oblique lattice;

2) |a| < |b| < |a-b| = |a+b|

- rectangular lattice;

3) (i) |a| < |b| = |a-b| < |a+b|

(ii) |a| = |b| < |a-b| < |a+b|, (by the replacement of b and a-b we obtain (i))

- centered rectangular lattice;

4) |a| = |b| < |a-b| = |a+b|

- square lattice;

5) |a| = |b| = |a-b| < |a+b|

- hexagonal lattice.

So there are 5 types of lattices:

- oblique;

- rectangular;

- centered rectangular;

- square;

- hexagonal.

All the lattices except centered will be called simple lattices.

The Theorem 3.1 and the discreteness condition restrict the possibilities for O_K to a finite number of different rotations that may belong to O_K for any wallpaper group K. By proving the Crystallographic Restriction Theorem, we will show that there are allowed only four non-trivial rotations through the angles [(2p)/ 6], [(2p)/ 4], [(2p)/ 3], [(2p)/ 2], i.e. the rotations of the order 6, 4, 3, 2, respectively.

Every orthogonal group of a wallpaper group is finite, because the wallpaper group is discrete, so it contains the rotations through the angles [(2p)/ k], k Î Z. Since the vectors a and b that generate T_K are independent, they represent the basis of R². In this basis, according to Theorem 3.1, the matrix from O_K preserves the lattice (this matrix represents the rotations about the origin), and it will contain the integer values (as lattice nodes). It's trace will be integer to. Because a matrix trace is invariant under the change of basis, and in standard basis the trace of

M =

æ
ç
è

cosq -sinq

sinq cosq

ö
÷
ø

tr(M) = 2cosq,

all the terms 2cosq will be integers. Therefore,

cosq =

æ
ç
ç
ç
ç
ç
ç
ç
è

for

q =

for

q =

±1

for

q = 0,

We proved:

Crystallographic Restriction Theorem. In a wallpaper group, the point group of rotations must be of order 1, 2, 3, 4 or 6.

This theorem is stated by Barlow in 1893 [6].

By using the proved existence of five lattice forms, four possible non-trivial rotations (Crystallographic Restriction Theorem) and the fact that these rotation preserve a lattice (Theorem 3.1), we will demonstrate the existence of 17 non-isomorphic wallpaper groups. Their classification will be done by exhausting all possible cases: for every combination of a lattice and a orthogonal group we will construct the corresponding group, or show that such a group does not exist. At the end, we will prove that all groups derived are mutually non-isomorphic.

We will use the standard notation, where the letters p or c denote a primitive or centered lattice, respectively. The number following the letter gives the order of rotation. It is followed by the next letter: m for reflection, g for glide reflection. This scheme has some exceptions: the groups p3m1 and p31m. That disagreement comes from the older notation that used four symbols.

In that classification, we will consider the vector a as collinear to x-axis, and b in the first quadrant. By M_q will be denoted the matrix of rotation about the origin, through the angle q, and S_f will be a reflection in the line passing through the origin, and of the slope f/2 .

Let`s mention that for every T_K and it's orthogonal group O_K, the wallpaper group will be T_KÈ_{X_i}_Î_{O_K}(t,X), where tÎ T_K and (t,X_i) represents the realization of X_i from O_K in K.

We begin the classification from the oblique lattice:

(1) As for the oblique lattice R, |a| < |b| < |a-b| < |a+b|,

the only element of O_D that preserves R is the rotation through f about the origin, so

O_K Ì {±I}.

(i) If the only rotation in K is the identity I, we get the simplest case: the wallpaper group generated by translations, K = {(ma+nb,I) | m,nÎZ}.

According to the notation accepted, this is the wallpaper group p1. It's orthogonal group is trivial.

(ii) O_K contains -I. We get K = T_K{(0,I),(0,-I)}, that is the union of two neighboring classes of T_K. The elements of K, not belonging to T_K are (ma+nb,I)(0,-I) = (ma+nb,-I), m,nÎ Z (that means that the elements are translations and half-turns about the points (¹/₂ma+¹/₂nb)).

Here, K is the wallpaper group p2. The orthogonal group is C₂.

(2) Rectangular lattice:

|a| < |b| < |a-b| = |a+b|,

Here, except the coincidence, we have the transformations -I, S₀ and S_p preserving the lattice:

(i) For O_K = {I,S₀} there are two possibilities:

a) S₀ is realized in K as a reflection (0,S₀). K = T_KÈT_K(S₀), and we have the wallpaper group pm. It's orthogonal group is D₁.

b) S₀ is realized in K as a glide reflection, so K contains (0,S₀). This is the glide reflection (¹/₂a,S₀).

Let that glide reflection be given in the form (aa+bb,S₀). Then (aa+bb,S₀)²=( aa +bb+aa-bb,I)=((2aa,I) ÎT_KÞ a = ^m/₂, m Î Z. For m even, we will have (¹/₂ka,I)(¹/₂ka,S₀) ÎT_KÞ (0,S₀) Î T_K, and S₀Ï O_K, so this is the contradiction. Hence, m is odd, and the glide reflection is of the form (ma+nb,I)(¹/₂a,S₀). The group K we obtain as T_KÈT_K(¹/₂a,S₀).

This is the wallpaper group pg. It's orthogonal group is D₁.

(ii) Orthogonal group

O_K is {I,-I, S₀, S_p }

For O_K = { I,S_p} we get the group isomorphic to a). Therefore, O_K Ì { S₀,S_p}. As

(0,S₀)(0,S_p) = (0,S₀S_p),

S₀S_p =

æ
ç
è

-1

ö
÷
ø

æ
ç
è

-1

ö
÷
ø

æ
ç
è

-1

ö
÷
ø

= -I.

We have -I Î O_K. According to that, there are three wallpaper group corresponding to this orthogonal group:

a) If S₀ and S_p are realized as reflections, K = T_KÈ_{XÎO_K}(0,X). This is the wallpaper group pmm.

It's orthogonal group is D₁×D₁.

b) The only element of orthogonal group realized as a reflection is (0,S_p). Now K must contain the glide reflection parallel to the y-axis. By analogy with (1), we obtain that the glide reflections are of the form (¹/₂,S₀). The transformation -I from O_K is realized as (¹/₂,S₀)(0,S_p) = (¹/₂a,-I). K = T_KÈT_K(0,S₀)ÈT_K(0,S_p)ÈT_K(¹/₂a,-I). This is the wallpaper group pmg.

The orthogonal group is D₁×D₁.

c) The third case occurs when K does not contain the reflections. So, S₀ is realized as (¹/₂a,S₀), and S_p as (¹/₂b,S_p). -I is realized as (¹/₂a,S₀)(¹/₂b,S_p) = (¹/₂(a-b),-I).

K = T_KÈT_K(¹/₂a,S₀)ÈT_K(¹/₂b,S_p)ÈT_K(¹/₂(a-b),-I).

This is the wallpaper group pgg. It's orthogonal group is D₁×D₁.

(3) Centered lattice

|a| < |b| = |a-b| < |a+b|

The elements of O_K as in (2) are I, -I, S₀, S_p.

Since |b| = |a-b|, for a = (x_a,y_a) and b = (x_b,y_b) holds:

x_b²+y_b² = (x_a-x_b)²+(y_a-z_b)²Û 2x_bx_a-x_a²+2y_by_a-y_a² = 0 Û x_a(2x_b-x_a)+y_a(2y_b-y_a) = 0

Û áa,2b-añ = 0 Û 2b-a ^a Þ 2b-a

so we obtain again the rectangular lattice.

To avoid the groups isomorphic to the already derived ones (pm, pg, pmm, pmg), we take that K, where the reflections from O_K are realized as both reflections and glide reflections.

Namely such O_K are characteristic for the centered lattice, in order to make a difference between the centered and the rectangular lattice.

(i) In the case that O_K = { I,S₀}, S₀ is realized as a reflection (2b-a,S₀), and glide reflection as (¹/₂(2b-a)+^a/₂,S₀) = (b,S₀), we have K = T_KÈT_K(b,S₀).

This is the wallpaper group cm. The structure of O_K for this group is D₁.

(ii) The case when O_K={ I,-I,S₀,S_p } is analogous to (i) (by mutually exchanging x- and y-axis).

Hence, we have K = T_KÈT_K(b,S₀)ÈT_K(a,S_p ).

The wallpaper group derived is cmm. It's orthogonal group is D₁×D₁.

4) Square lattice

It is preserved by the dihedral group D₄. Therefore,

|a| = |b| < |a-b| = |a+b|

To get the wallpaper groups characteristic for this lattice (non-isomorphic to already derived ones) O_K must contain M_[(p)/
2].

(i) In the case O_K = áM_[(p)/
2]ñ we have

K = T_KÈT_K(0,M_[(p)/
2])ÈT_K(0,M_p)ÈT_K(0,M_[(3p)/
2]).

The result is the wallpaper group p4. The structure of it's orthogonal group is C₄.

(ii) In the case S₀ ÎO_K, O_K = {I,M_[(p)/2],-I,M_[(3p)/
2], S₀,S_[(p)/
2],S_p,S_[(3p)/
2]},

because of

S₀M_[(p)/
2] =

æ
ç
è

-1

ö
÷
ø

æ
ç
è

-1

ö
÷
ø

æ
ç
è

-1

ö
÷
ø

= S_{[(p)/ 2]}

a) S₀ is realized as a reflection.

We get the wallpaper group p4m. It's orthogonal group is D₄.

b) S₀ is not realized as a reflection. Let S₀ be realized as (aa+bb,S₀). So

(aa+bb,S₀)² = (2a,S₀) ÎK

It follows that 2a ÎZ. If a is an integer, we have (-aa,I)(aa+bb,S₀) = (bb,S₀) ÎK, and that is the contradiction. Therefore, S₀ is realized as (¹/₂ a+bb,S₀). By analogy, S_p is realized as (a₁ a+¹/₂b,S₀). From

(

a+bb,S₀)(a₁a+

b,S_p) = ((a₁ +

)a+(b-

)b,M_p)

it follows that a₁ = ¹/₂+k and b = ¹/₂+l, where k, l Î Z.

K = T_KÈT_Ká(0,M_[(p)/
2])ñÈT_K(

b,S₀)ÈT_K(

b,S_[(p)/2])ÈT_K(

b,S_p)ÈT_K(

b,S_[(3p)/
2])

This is the wallpaper group p4g. It's orthogonal group is D₄.

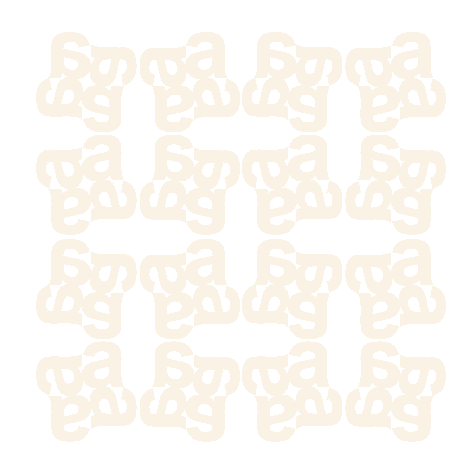(6) Hexagonal lattice

There we have the lattice:

|a| = |b| = |a-b| < |a+b|,

and it is preserved by the dihedral group D₆, generated by M_{[(p)/ 3]} and S₀ from O_K. In the subgroup of direct transformations from D₆, we have áM_[(2p)/3]ñ£áM_[(p)/
3]ñ. Except S₀, the indirect transformations in D₆ are S_[(kp)/
3], k = 1,¼,5 .

Since S₀M_[(kp)/
3] = S_{[(kp)/ 3]}. Each of them is realized as a reflection in K.

It is sufficient to prove that S₀ is realized as the reflection (for (0,S₀)(0,M_[(kp)/
3]) = (0,S_{[(kp)/ 3]})). Let S₀ be realized as (aa+bb,S₀). Then

(0,M_{[(2p)/ 3]})(aa+bb,S₀) = (a(b-a)-ba,S_[(2p)/
3]) Î K.

(a(b-a)-ba,S_[(2p)/
3])² = ((a-b)b,I) ÎKÞ a-bÎ Z Þ (aa+bb,S₀)((b-a)a,I) = (b(a+b),I) ÎKÞ a,bÎ Z Þ (aa+bb,S₀)(-aa,I) = (bb,S₀) ÎK, i.e. S₀ is realized as the reflection in K.

When O_K = áM_[(2p)/
3],S_{[(p)/ 3]}ñ, S₀ is not in O_K.

Now we see that the wallpaper groups corresponding to the hexagonal lattice are:

(i) O_K is generated by M_[(p)/
3]. Here

K = T_K

È
k = 1,¼,5

(0,M_{[(kp)/ 3]})

This is the wallpaper group p6. It's orthogonal group is C₆.

(ii) The orthogonal group is D₆, O_K = áM_[(p)/3],S₀ñ.

K = T_K

È
k = 1,¼,5

(0,M_{[(kp)/ 3]})

È
k = 1,¼,5

(0,S_{[(kp)/ 3]})

The wallpaper group K is p6m, and it's orthogonal group is D₆.

(iii) O_K is generated by M_[(2p)/
3].

K = T_K

È
k = 1,¼,3

(0,M_{[(2kp)/ 3]})

The obtained wallpaper group is p3, and the orthogonal group is isomorphic to C₃.

(iv) When O_K is generated by M_[(2p)/
3] and S₀:

K = T_K

È
k = 1,¼,3

(0,M_{[(2kp)/ 3]})

È
k = 1,¼,3

(0,S_{[(2kp)/ 3]})

This wallpaper group is p3m1, and it's orthogonal group is isomorphic to D₃.

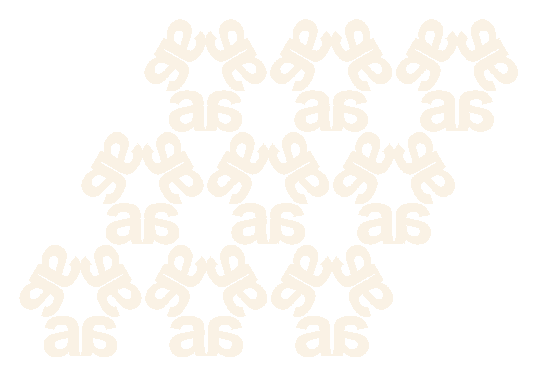(v) O_K = áM_[(2p)/
3],S[(p)/ 3] ñ.

K = T_K

(0,M_{-[(2p)/ 3]})

T_K(0,M_-[(2p)/
3])

T_K(0,S_[(p)/
3])

T_K(0,S_[(5p)/
3])

T_K(0,S_p).

This is the group p31m, and the orthogonal group is D₃.

In the presented analysis we distinguished 17 different cases for the wallpaper groups: 2 for the oblique, 6 for rectangular, 7 for centered, 11 for square, and 11 for hexagonal lattice. For completing the classification, we need to show that these groups are not mutually isomorphic.

The only possible isomorphic groups can be those with isomorphic orthogonal groups (Theorem 3.2, Corollary 3.1). So, the groups of the following classes (p2, pm, pg, cm), (pmm, pmg, pgg, cmm), (p4m, p4g; p3m1, p31m) might be mutually isomorphic.

In the first class, the only group possessing a rotation is p2, so it is not isomorphic to any other group of that class (Theorem 3.2). The group pg is the unique group of that class which does not posses reflections, so it is not isomorphic to pm or cm. The remaining groups pm and cm are not mutually isomorphic, because every glide reflection from pm can be decomposed as the product of translations and reflections from pm (Theorem 3.2, Corollary 3.2), which is not true for cm.

The group pgg does not contain the reflections, so it is not isomorphic with pmm, pmg or cmm. The groups pmg and cmm are not isomorphic, because the product of every two reflections from pmg is a translation, while in cmm this product can give -I (Theorem 3.2, Corollary 3.3). Finally, the group pmm is not isomorphic with pmg or cmm, because every glide reflection from pmm can be decomposed as the product of translations and reflections belonging to that group (Theorem 3.2, Corollary 2), which not holds for pmg or cmm.

Every rotation from p4m can be decomposed as the product of two reflections from p4g, but this is not true for p4g. Therefore, p4m and p4g are not isomorphic (Theorem 3.2, Corollary 3.2).

In the same way, the previous consideration holds for p31m and p31m.

Thus, the classification of 17 wallpaper groups is completed.

Theorem 3.3.2. There are 17 different wallpaper groups.

The first attempt to derive and classify the wallpaper groups we may find in the works of C. Jordan (1867/1869), but he omitted the group pgg, recognized by L. Sohncke in 1874. The first complete classification of wallpaper groups was done by E.S. Fedorov in 1890 [6].

3.3 The Wallpaper Groups

NEXT