Occurrence of square faces in composite forms relative to icosahedral and cubic point groups

Livio Zefiro
Dip.Te.Ris., Universita' di Genova, Italy
(E-mail address: livio.zefiro@fastwebnet.it)

Notes
  • Tested with Internet Explorer 8, Mozilla Firefox 3.6, Opera 10.6 and Google Chrome at 1024x768 and 1280x1024 pixels
  • All the images were created by SHAPE 7.0, a software program for drawing the morphology of crystals, distributed by Shape Software
  • Hovering with the mouse on the images, the symbol of a pointer appears: if your web browser is set up to visualize VRML files, by clicking with the left button of the mouse it should be possible to visualize in a new window the corresponding dynamic image, that can be rotated, shifted, enlarged...
    Cortona 3D Viewer is a good Web3D visualizer, that can be downloaded from here; at present it is working also with the last releases of the main browsers.

INTRODUCTION
The presence of square faces, rather common in composite forms of crystals belonging to the cubic system, is surely less usual in quasi-crystals having icosahedral symmetry.
This work is a review of the conditions leading to the occurrence of square faces in cubic and icosahedral composite forms: the faces that can assume more easily a square shape are faces of cube or rhomb-dodecahedron in the first case, and faces of rhomb-triacontahedron or deltoid-hexecontahedron in the second case. Even if with increasing difficulty, due to the need of simultaneous occurrence of particular geometric conditions, also the faces of tetrakis-hexahedron, deltoid-icositetrahedron or triakis-octahedron (in the first case) and triakis-icosahedron or pentakis-dodecahedron (in the second case) can have a square shape. It happens when the ratios between the distances of the different faces from the center of the solid (hereinafter referred to as "central distances") assume appropriate values.

OCCURRENCE OF SQUARE FACES IN COMPOSITE FORMS BELONGING TO THE CUBIC POINT GROUPS
Seven are the different kinds of single forms relative to each point group of the cubic system. Concerning both 4/m 3 2/m and  432 point groups [1], in four cases square faces can be generated by the intersection of a cube with another single form:
Concerning the first three cases, the same thing happens also in 2/m3 point group, whereas the fourth case is relative also to 43m point group.

Archimedean truncated octahedron
d{111}/ d{100}=√3/2
In general square faces of cube can be obtained when √3/2 ≤ d{100}/d{111}<√3

Cuboctahedron, obtained from the intersection of a cube with an octahedron when d{100}/d{111}=√3/2
Truncated cubes, in which square faces are absent, are instead obtained when:
 √3/3<d{100}/d{111}<√3/2 

Intersection of a cube {100} with a rhomb-dodecahedron {110}.
The ratio between the central distances d{100}/d{110} must be greater than √2/2 and less than √2

Intersection of the cube {100} with the deltoid-icositetrahedron {211}.
In general, square faces can be obtained when the ratio d{100}/d{hkk} is equal or greater than √1+2(k/h)2/(1+k/h) and less than √1+2(k/h)2

Intersection of the cube with the deltoid-icositetrahedron {211} when the ratio d{100}/d{211}= √1+2(1/2)2/(1+1/2) = √2/3.
This composite form can be derived from the cuboctahedron by the substitution of each its triangular face with a trigonal pyramid.
Intersection of the cube {100} with the tetrakis-hexahedron {210}.
In general, the ratio d{100}/d{hk0} must be greater than √1+(k/h)2/(1+k/h) and less than √1+(k/h)2

In the 23 point group, square faces of cube can be obtained from the intersection of a cube with two other single forms:
Concerning the first three cases, the same thing happens also in the 43m point group, whereas the fourth case is relative also to the 2/m3 point group.
 

Square faces of cube obtained, in the 23 point group, by the intersection of three single forms
Cube {100}
Tetrahedron  {111}
Tetrahedron  {111}		 Cube {100}
Tetrahedron  {111}
Triakis-tetrahedron {211}
Cube {100}
Triakis-tetrahedron {411}
Triakis-tetrahedron {211}		 Cube {100}
Pentagon-dodecahedron {210}
Pentagon-dodecahedron {401}

Square faces of cube cannot be generated by the intersection of a cube with any {hhk} form where k<h, that is, depending on the symmetry of the different cubic point groups, a  triakis-octahedron or a deltoid-dodecahedron.
Concerning {hkl} forms, in case of the 432 point group the intersection of a cube with any gyroid (also named pentagonal icositetrahedron) can again generate square faces when the ratio of the central distances is included in a certain range, variable in function of each gyroid.
The simultaneous intersection of a cube with an appropriate gyroid and an octahedron, when the ratio of their central distances is:
dgyroid /dcube = doctahedron /dcube = 1.0619,
leads to another Archimedean semiregular polyhedron, the snub-cube: six out of its thirty-eight faces have the shape of squares, the remaining thirty-two have the shape of equilateral triangles (eight of the triangular faces derive from the octahedron, the other twenty-four from the gyroid).
Steps leading to the snub-cube, starting from the intersection of a cube with an appropriate gyroid and through an intermediate step, in which each vertex of the square is shared with three kite-shaped faces of the gyroid. The further intersection with an octahedron, having the same central distance of the gyroid, gives as result the snub-cube.
Each vertex of the snub-cube is shared by a square and four equilateral triangles: the square comes from the cube, the red triangle from the octahedron whereas the other three blue triangles derive from the gyroid.

An analoguous composite form including square faces of cube can be obtained in the 23 point group, substituting the gyroid {hkl} with two congruent tetrahedral pentagon-dodecahedra {hkl} and {hlk} (having the same central distance); the two tetrahedral pentagon-dodecahedra can be even dissimilar (with different central distances), on condition that the directions of the edges deriving from the intersection of their faces with the faces of cube are orthogonal. Relatively to both cases, the views along the [100] direction, normal to a square face, are shown in the next image.

Square faces of cube obtained, in the 23 point group, by the intersection with two tetrahedral pentagon-dodecahedra

Cube {100}
 Tetrahedral pentagon-dodecahedron {421}
 Tetrahedral pentagon-dodecahedron {412}
The two congruent tetrahedral pentagon-dodecahedra have the same central distance

Cube {100}
Tetrahedral pentagon-dodecahedron {421}
 Tetrahedral pentagon-dodecahedron {524}
The two different tetrahedral pentagon-dodecahedra have also different central distance

It is instead impossible to obtain a square face from the intersection of the cube con any {hkl} general form in 4/m 3 2/m and 43m point groups.

 Relatively to the intersections among the three simplest cubic forms, namely cube, octahedron and rhomb-dodecahedron, one can identify the conditions leading to the occurrence of square faces of cube or rhomb-dodecahedron in the resulting composite forms.

Square faces of cube are always present in composite forms, derived from the intersection of a cube, an octahedron and a rhomb-dodecahedron, when the relation between the central distances of cube and octahedron is the following:
dcube= 2√2 -√3·doctahedron (valid in the ranges √2/2 < dcube<√2 and √6/3 < doctahedron<√6/2)
if one attributes an unit value to the central distance of the rhomb-dodecahedron.
 The faces of octahedron have always the shape of equilateral triangles (whose size is in inverse proportion to the size of the squares), whereas the faces of rhomb-dodecahedron have, in general, a rectangular shape.
The faces of rhomb-dodecahedron become square only when dcube=1 (and doctahedron= (2√6-√3)/3, in consequence of the previous relation); since in such a circumstance all the faces have the shape of regular polygons, the resulting composite form is the Archimedean rhombicuboctahedron (central view of the following set of three images).


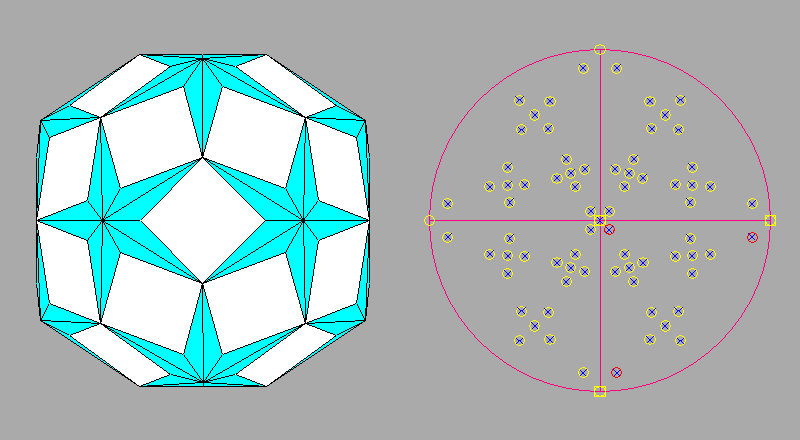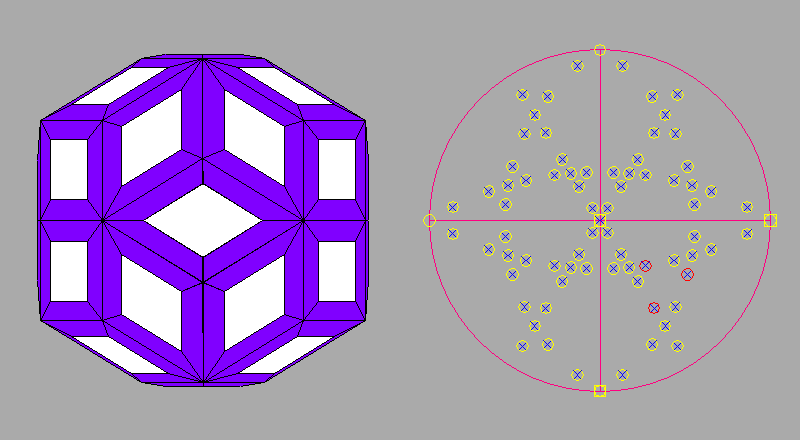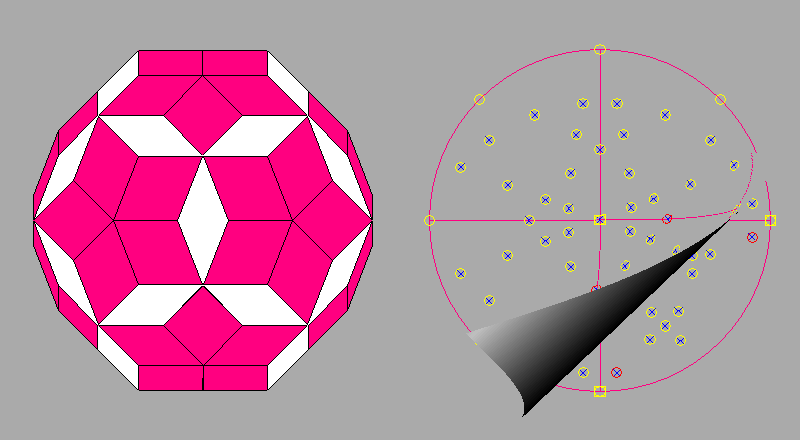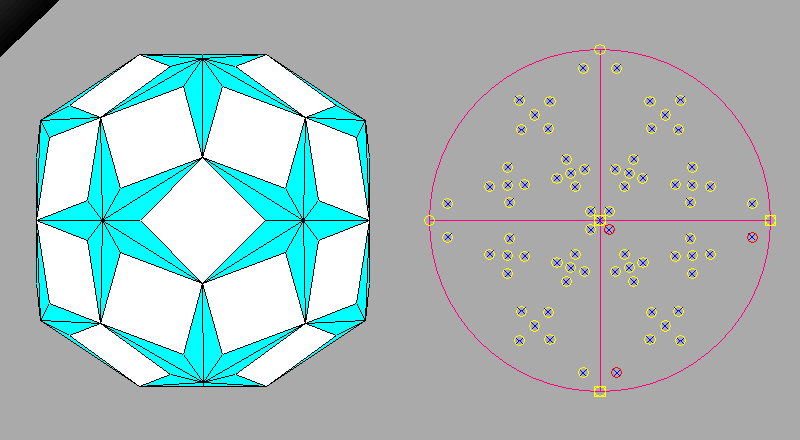
Square faces of rhomb-dodecahedron are always present in composite forms when the relation between the central distances of cube and octahedron is the following:  dcube = (√2/2 -1)+(√6/2)·doctahedron assuming, also in this case, an unit value of the central distance of the rhomb-dodecahedron.
The relation holds in the ranges √2/2<dcube ≤1 and √6/3 <doctahedron≤ (2√6-√3)/3: the corresponding polyhedra go from the cuboctahedron to the rhombicuboctahedron (already reported in the previous image).
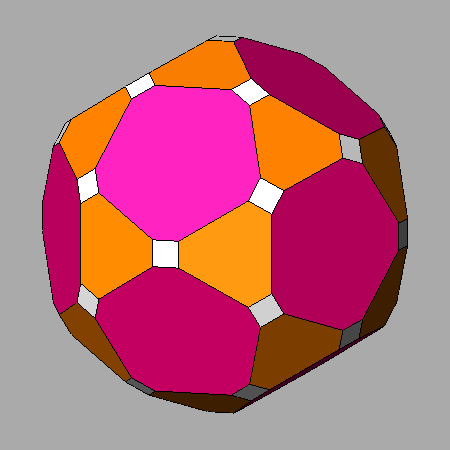
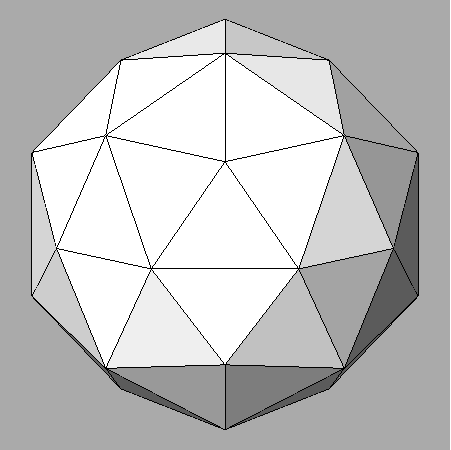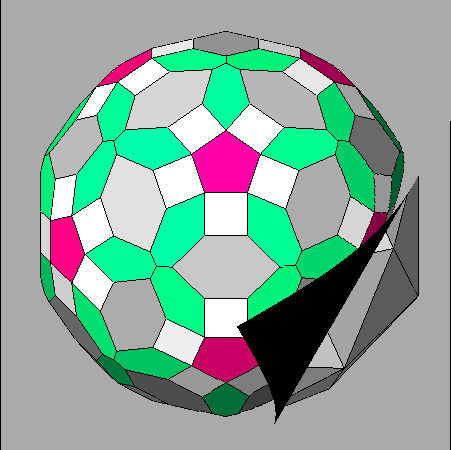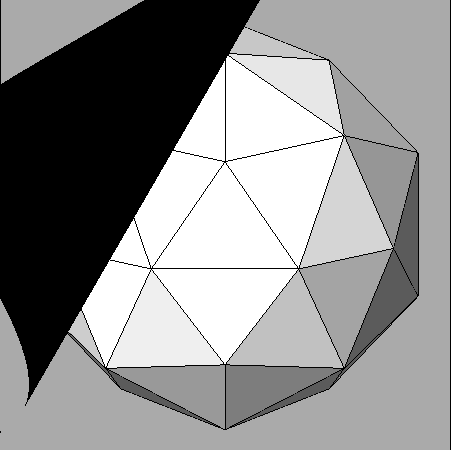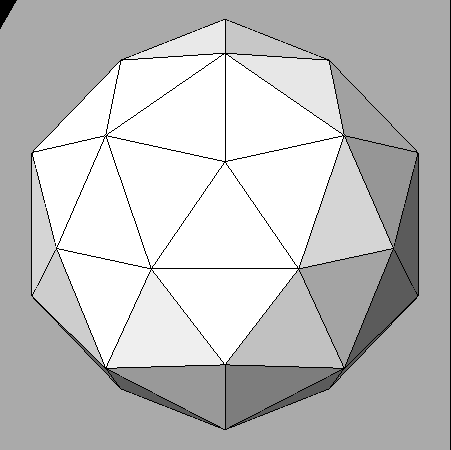
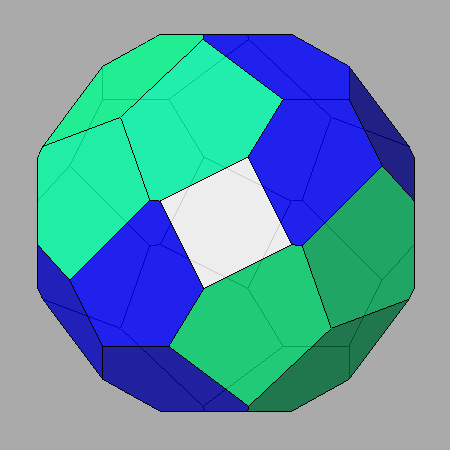
The central view of the following set of three images concerns the Archimedean truncated cuboctahedron in which, in addition to the square rhomb-dodecahedral faces, the cubic and octahedral faces have the shape of regular octagons and hexagons, respectively.


As already pointed out, the rhombicuboctahedron is characterized simultaneously by square faces of cube and square faces of rhomb-dodecahedron, since both relations between dcube and doctahedron concern it.

Composite forms, derived from the rhombicuboctahedron, in which the faces of rhomb-dodecahedron are square, can be obtained by the following procedures:
  • substitution of the only octahedron with a triakis-octahedron: in this case also square faces of cube are present
  • substitution of the only cube with a tetrakis-hexahedron
  • substitution of both octahedron and cube with a triakis-octahedron and a tetrakis-hexahedron, respectively.
    •  
    Further square faces of rhomb-dodecahedron in composite forms can be obtained by an appropriate decrease of the central distances of the previous forms intersecting the rhomb-dodecahedron.

    Rhomb-dodecahedron {110}
    Triakis-octahedron {221}
    Cube {100}

    		 Rhomb-dodecahedron {110}
    Octahedron {111}
    Tetrakis-hexahedron {210}    		 Rhomb-dodecahedron {110}
    Triakis-octahedron {221}
    Tetrakis-hexahedron {210}

    The simultaneous presence in a solid of square faces of cube and rhomb-dodecahedron can be obtained from the previous set of three composite forms by the addition, in the first case, of the deltoid-icositetrahedron {211} and the  tetrakis-hexahedron {320} (the square faces of cube in such composite form result to be 45° rotated with respect to the usual orientation of the cube), and by the only addition, in the other two cases, of the cube.
     

    Rhomb-dodecahedron {110}
    Triakis-octahedron {221}
    Cube {100}
     Deltoid-icositetrahedron {211}
    Tetrakis-hexahedron {320}

    		 Rhomb-dodecahedron {110}
    Octahedron {111}
    Tetrakis-hexahedron {210}
    Cube {100}    		 Rhomb-dodecahedron {110}
    Triakis-octahedron {221}
    Tetrakis-hexahedron {210}
    Cube {100}

    In conclusion, the following three examples concern the possible presence, in composite forms, of square faces belonging to:
  • a tetrakis-hexahedron {210}
  • a triakis-octahedron {221}
  • a deltoid-icositetrahedron
    • {211}
    by their simultaneous intersection with three other forms:
  • a rhomb-dodecahedron
  • a cube or an octahedron
  • a different deltoid-icositetrahedron

    • in case of appropriate ratios of the central distances of the faces belonging to the different forms.

    Tetrakis-hexahedron {210}
     Rhomb-dodecahedron {110}
    Cube {100}
     Deltoid-icositetrahedron {211}

    		 Triakis-octahedron {221}
    Rhomb-dodecahedron {110}
     Octahedron {111}
     Deltoid-icositetrahedron {311}    		 Deltoid-icositetrahedron {211}
     Rhomb-dodecahedron {110}
     Octahedron {111}
     Deltoid-icositetrahedron {411}

     
    OCCURRENCE OF SQUARE FACES IN COMPOSITE FORMS BELONGING TO 2/m3 5 AND 235 ICOSAHEDRAL POINT GROUPS
     
    The higher symmetry, respect to cubic point groups, that characterize both 2/m 3 5 and 235 icosahedral point groups ( together with the absence of 4-fold axes) somehow thwarts the presence of square faces in icosahedral composite forms.
    Actually the unique way of obtaining square faces by the intersection of only two forms involves the rhomb-triacontahedron {100} and a {hkk} form provided that h/k ≥ τ3, where τ corresponds to the golden ratio (1+√5)/2.
    When h/k =τ3, in both icosahedral point groups the resulting form is the Catalan deltoid-hexecontahedron {τ311} (or {τ2 1/τ 1/τ}), whereas, in the only 2/m 3 5 icosahedral point groups, the {hkk} forms characterized by h/k > τ3 correspond to a series of hexakis-icosahedra, all belonging to the zone of the direction [011]; in particular, the {2+τ2 1/τ 1/τ} form corresponds to the Catalan hexakis-icosahedron.
    One can find in the Appendix a detailed description of what happens when the ratio h/k in the {hkk} forms is less than τ3.

    Square faces of rhomb-triacontahedron {100} deriving from the intersection with the Catalan deltoid-hexecontahedron {τ2 1/τ 1/τ} or the Catalan hexakis-icosahedron {2+τ2 1/τ 1/τ}

    Rhomb-triacontahedron {100} and Catalan deltoid-hexecontahedron {τ2 1/τ 1/τ} having the same central distance

    Rhomb-triacontahedron and Catalan deltoid-hexecontahedron sharing vertices

    d{τ2 1/τ 1/τ}/d{100}= 1.0341

    Rhomb-triacontahedron {100} and Catalan  hexakis-icosahedron {2+τ2 1/τ 1/τ} having the same central distance

    		 Rhomb-triacontahedron and Catalan hexakis-icosahedron sharing vertices
    d{2+τ2 1/τ 1/τ}/d{100}= 1.0323

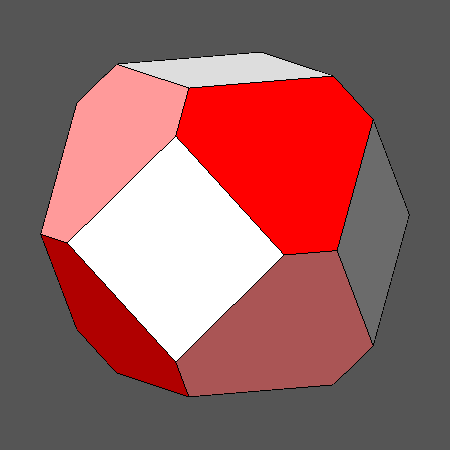
    Square faces of rhomb-triacontahedron can be obtained also when, in a composite form, the rhomb-triacontahedron intersects two other polyhedra: alternatively, a dodecahedron or a pentakis-dodecahedron and an icosahedron or a triakis-icosahedron.
    The simplest case consist in the intersection of a Catalan rhomb-triacontahedron, whose central distance has an unit value, with two Platonic solid, a dodecahedron and an icosahedron, whose central distances, included in the ranges:

     1/√1+1/τ2  < ddodecahedron ≤ 1/√1+1/τ2 ·(1+1/τ4)
    and
    τ /√3 < dicosahedron ≤ τ/√3 ·(1+1/τ5)
     
    are put into correspondence, as shown in [2],  by the relation:
     
    ddodecahedron = (1/√1+1/τ2)·(√3 dicosahedron - 1/τ )
     
    When the values of the central distances of the dodecahedron and the icosahedron correspond to the lower limits of the ranges previously defined :
     
     ddodecahedron  = 1/√1+1/τ2 = 0.8507
    and
    dicosahedron = τ /√3 = 0.9342
     
    the polyhedron resulting from their intersection is an icosidodecahedron. As a matter of fact, the faces of the rhomb-triacontahedron having an unit central distance would be exactly tangent to the vertices of the icosi-dodecahedron.
    In consequence of increasing values of the central distances of dodecahedron and icosahedron (and constant drhomb-triacontahedron = 1), one obtains square faces of rhomb-triacontahedron with increasing area, together with decagonal faces of dodecahedron and hexagonal faces of icosahedron which, in general, are not regular.
    Such faces have indeed the shape of regular decagons and hexagons only when:
     
     ddodecahedron = 1/√1+1/τ2 ·(1+1/(τ5 +1)) = 0.9210
    and
    dicosahedron = τ /√3 ·(1+1/(τ6 +1)) = 0.9819

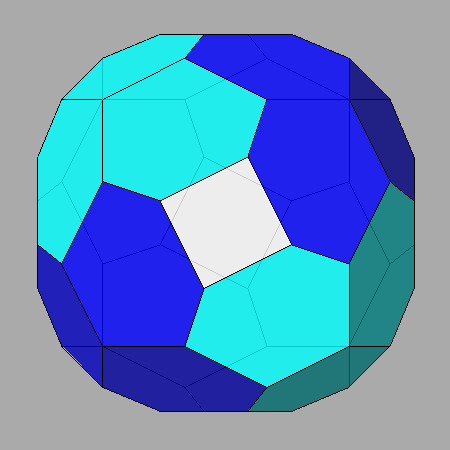
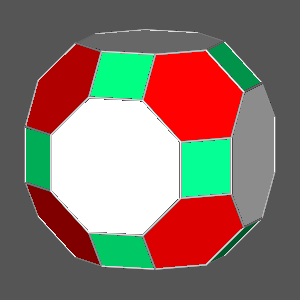
    and the resulting solid is the Archimedean truncated icosi-dodecahedron, misleading name since it cannot be obtained simply by a truncation of the icosi-dodecahedron [2]: then, alternatively, it is also called great rhombicosidodecahedron.

    When the central distances of dodecahedron and icosahedron attain the maximum value of the respective ranges previously defined:
     

    ddodecahedron  = 1/√1+1/τ2 ·(1+1/τ4) = 0.9748
    and
    dicosahedron = τ /√3 ·(1+1/τ5) = 1.0184

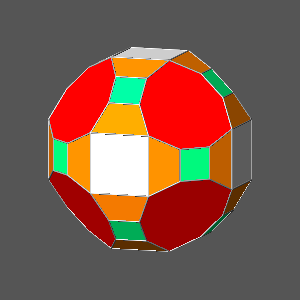
    the shapes of the faces of dodecahedron and icosahedron become regular pentagons and triangles, respectively, and the resulting solid is the Archimedean rhombicosidodecahedron.
    Four examples of composite forms including square faces of rhomb-triacontahedron (together with faces of dodecahedron and icosahedron) are shown in the following figure; in particular, in the forms of the left column the faces of dodecahedron and icosahedron have the shape of non regular polygons, whereas the two Archimedean polyhedra are reported in the right column.


    Square faces of rhomb-triacontahedron in presence of decagonal faces of dodecaheron and hexagonal faces of icosahedron which are both regular only in case of the truncated icosi-dodecahedron and become regular pentagons and triangles, respectively, in case of the rhomb-icosidodecahedron.
    The values, reported in the captions, of the central distance of the faces of dodecahedron and icosahedron refer to a unit value of the central distance of the square faces of rhomb-triacontahedron.
    ddodecahedron = 0.8887   dicosahedron = 0.96
    Archimedean truncated icosidodecahedron
    ddodecahedron = 0.9210   dicosahedron = 0.9819
    ddodecahedron = 0.9476   dicosahedron = 1.0
    Archimedean rhomb-icosidodecahedron
    ddodecahedron = 0.9748   dicosahedron = 1.0184

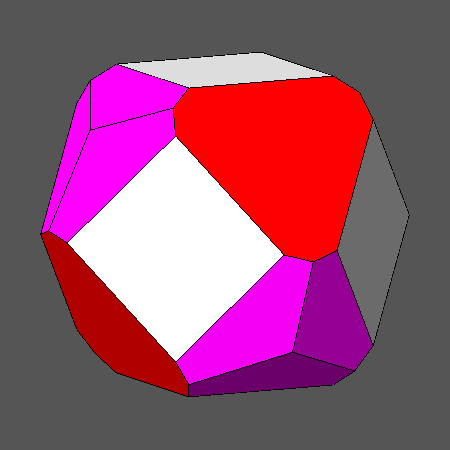
    A series of composite forms including square faces of rhomb-triacontahedron can be obtained starting from the Archimedean rhomb-icosidodecahedron, by the substitution of the icosahedron with a triakis-icosahedron and/or the substitution of the dodecahedron with a pentakis-dodecahedron.
    In the next figure, the icosahedron is always present in the forms of the left column, whereas it is replaced by the triakis-icosahedron {τ310} in the forms of the right column.
    The dodecahedron, always present in the forms of the first row, is replaced by the pentakis-dodecahedron {τ201} in the second row and by the pentakis-dodecahedron {τ301} in the third row.
     
    Square faces of rhomb-triacontahedron in composite forms derived from the Archimedean rhomb-icosidodecahedron
     a) rhomb-triacontahedron {100}
          dodecahedron {τ01}
         icosahedron {τ210}
     making the rhomb-icosidodecahedron     		b) rhomb-triacontahedron {100}
          dodecahedron {τ01}
         triakis-icosahedron {τ310}
     
    c) rhomb-triacontahedron {100}
        pentakis-dodecahedron{τ201}
        icosahedron {τ210}
    		d) rhomb-triacontahedron {100}
         pentakis-dodecahedron {τ201}
        triakis-icosahedron {τ310}
    e) rhomb-triacontahedron {100}
        pentakis-dodecahedron {τ301}
            icosahedron {τ210}
         		  f) rhomb-triacontahedron {100}
        pentakis-dodecahedron {τ301}
        triakis-icosahedron {τ310}

    One can note that only in the cases c) and f) of the previous set of images the square faces of rhomb-triacontahedron derive from the intersection with couples of faces characterized by permutated values of the indices and having consequently the same central distance; in detail, they are:

  • icosahedron {τ210} and pentakis-dodecahedron {τ2 01} in c)
  • triakis-icosahedron {τ310} and pentakis-dodecahedron {τ3 01} in
    •  f)
    In the other four cases the couples of faces intersecting each square face are placed at different central distances.

  • Another series of composite forms including square faces of rhomb-triacontahedron can be obtained starting from the Archimedean truncated icosidodecahedron by the substitution of the icosahedron  and/or the dodecahedron, respectively, with:
  • a couple of polyhedra made of a triakis-icosahedron and a deltoid-hexecontahedron having a symmetrical orientation in respect to the icosahedron
  • a couple of polyhedra made of a pentakis-dodecahedron and another deltoid-hexecontahedron having a symmetrical orientation in respect to the dodecahedron.

    • Square faces of rhomb-triacontahedron in composite forms derived from the Archimedean truncated icosidodecahedron

     a) rhomb-triacontahedron {100}
          dodecahedron {τ01}
         icosahedron {τ210}
     making the truncated icosidodecahedron     		 b) rhomb-triacontahedron {100}
          dodecahedron {τ01}
         triakis-icosahedron {3τ+1 1 0}
         deltoid-hexecontahedron {7τ-2 3τ+1 0}
    c) rhomb-triacontahedron {100}
        pentakis-dodecahedron{3τ  0 1}
        deltoid-hexecontahedron {7τ-8 τ2 0}
        icosahedron {τ210}
    		d) rhomb-triacontahedron {100}
         pentakis-dodecahedron     {3τ  0 1}
            deltoid-hexecontahedron {7τ-8 τ2 0}
        triakis-icosahedron {3τ+1 1 0}
        deltoid-hexecontahedron {7τ-2 3τ+1 0}

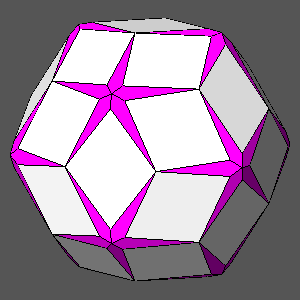
    Square faces of deltoid-hexecontahedron can be obtained in composite forms only in case of particular geometric conditions.
    Starting from the (τ10) face of the deltoid-hexecontahedron, its intersection with the (τ 1 1/τ) and (τ 1 -1/τ) faces of the rhomb-triacontahedron (as pointed out in the Table 1 of the Appendix, the rhomb-triacontahedron includes faces with both {100} and {τ 1 1/τ} indices) give rise to two edges, both parallel to the [1τ 0] direction.
    In order to obtain a square face of deltoid-hexecontahedron, two other faces must intersect each face of the deltoid-hexecontahedron along edges parallel to the [001] direction and therefore perpendicular to the two edges parallel to the [1τ 0] direction: in the more trivial case, such faces are the (1τ 0) face of the dodecahedron and the (τ 1/τ 0) face of the icosahahedron, placed at proper central distances.

    Steps leading to the formation of square faces of deltoid-hexecontahedron in a composite form including also dodecahedral, icosahedral and rhomb-triacontahedral faces
     a) deltoid-hexecontahedron {τ10}  b) deltoid-hexecontahedron {τ10}
              rhomb-triacontahedron {100}  
              d    100 /dτ 10 =  1.0028
    c) deltoid-hexecontahedron {τ10}    
        rhomb-triacontahedron {100}
        dodecahedron {1τ0}
        d1τ 0 /d    τ 10 = 1.0027    		  d) deltoid-hexecontahedron {τ10}
          rhomb-triacontahedron {100}
         dodecahedron {1τ0}
         icosahedron {τ 1/τ 0}
             dτ 1/τ  0 /d    τ 10 = 0.9996

    Also in this case, other composite forms including square faces of deltoid-hexecontahedron can be obtained starting from the previous polyhedron by the substitution of the icosahedron and/or the dodecahedron with a deltoid-hexecontahedron.
     
    Faces of deltoid-hexecontahedron having a square shape in composite forms which can include, together with a rhomb-triacontahedron, other deltoid-hexecontahedra in alternative with an icosahedron and/or a dodecahedron.
     a) deltoid-hexecontahedron {τ10}
         dodecahedron{1τ0}        
         icosahedron {τ210}
             rhomb-triacontahedron {100}      		  b) deltoid-hexecontahedron {τ10}
          dodecahedron{1τ0}
              deltoid-hexecontahedron {210} 
              rhomb-triacontahedron {100}
     c) deltoid-hexecontahedron {τ10} 
              deltoid-hexecontahedron {110} 
              icosahedron {τ210}
              rhomb-triacontahedron {100}    		  d) deltoid-hexecontahedron {τ10}
              deltoid-hexecontahedron {110}
              deltoid-hexecontahedron {210}  
              rhomb-triacontahedron {100}   

    At last, composite forms including square faces of deltoid-hexecontahedron can be obtained also by the substitution of the rhomb-triacontahedron, always present in the previous polyhedra, with a {hkl} hexakis-icosahedron in which the ratio h/k corresponds to τ.
    For example, in the following animated images the {τ 1 1/τ} face of the rhomb-triacontahedron is substituted by the {τ 1 1/τ2} face of the hexakis-icosahedron.
     
    Animated images showing the transition from rhomb-triacontahedral to hexakis-icosahedral faces in composite forms including square faces of deltoid-hexecontahedron
          deltoid-hexecontahedron {τ10} 
              dodecahedron{1τ0} 
              icosahedron {τ210}
              rhomb-triacontahedron {100} becoming a
          hexakis-icosahedron {τ 1 1/τ2}    		     deltoid-hexecontahedron {τ10}
            deltoid-hexecontahedron {110}
            deltoid-hexecontahedron {210}  
            rhomb-triacontahedron {100} becoming a
        hexakis-icosahedron {τ 1 1/τ2}

    In addition to the faces of rhomb-triacontahedron and deltoid-hexecontahedron, also the faces of triakis-icosahedron and pentakis-dodecahedron can assume a square shape, as shown in the following animated sequence (viewing direction along the normal to the (τ310) face of the triakisicosahedron, on the left, and (τ301) face of the pentakis-dodecahedron, on the right, respectively). In both cases it is required the presence of a rhomb-triacontahedron and an appropriate deltoid-hexecontahedron, together with a dodecahedron in case of the square faces of triakis-icosahedron or an icosahedron in case of the the square faces of pentakis-dodecahedron.

    Square faces resulting from the sequential truncation of a triakis-icosahedron (on the left) and a pentakis-dodecahedron (on the right), by a deltoid-hexecontahedron, an icosahedron or a dodecahedron, and a rhomb-triacontahedron.

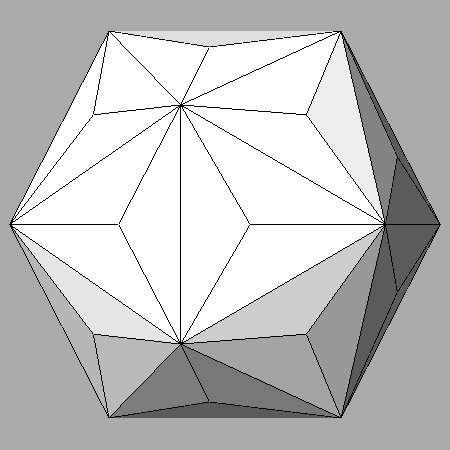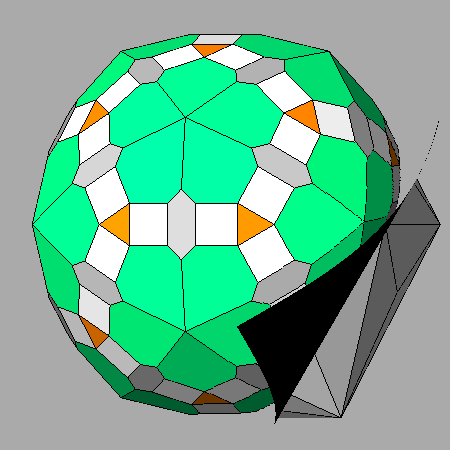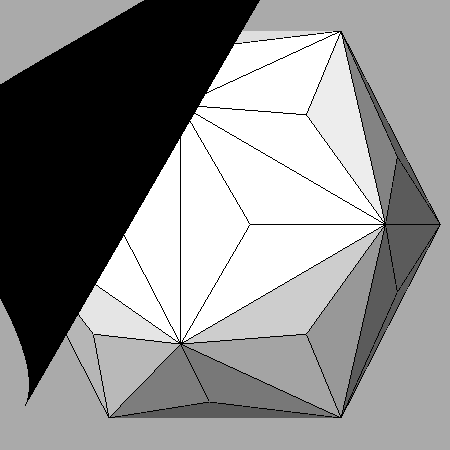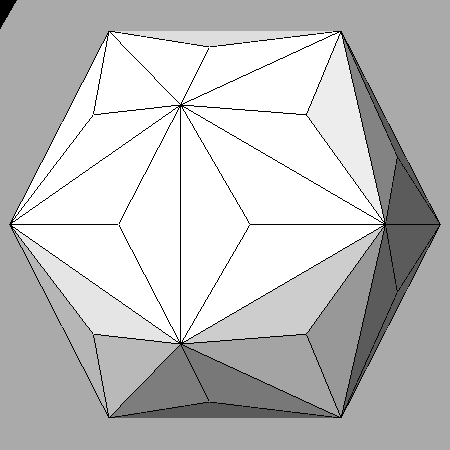
         triakis-icosahedron {τ310}
         deltoid-hexecontahedron {τ311}
         icosahedron {τ210}
         rhomb-triacontahedron {100}     		     pentakis-dodecahedron {τ301}
         deltoid-hexecontahedron {τ311}
         dodecahedron {τ01}
         rhomb-triacontahedron {100}

    Appendix
    It may be useful to remember that, as already pointed out in [2] and [3], the indices of all the faces of each icosahedral form can be obtained from the cyclic permutation of an only set of indices uniquely in case of dodecahedron, whereas the sets of indices are two, three or five in case of the other six icosahedral forms (see Table 1, where the indices of the Platonic and Catalan icosahedral forms belonging to the 2/m 3 5 point group are reported and compared with the indices of the corresponding Platonic and Catalan cubic forms belonging to the 4/m 3 2/m point group).

    Sets of {hkl} indices relative to the forms, belonging to 2/m 3 5 icosahedral and 4/m 3 2/m cubic point groups, which correspond to Platonic and Catalan polyhedra

    Icosahedral polyhedra

    		Indices {hkl} Cubic polyhedra Indices {hkl}
    Dodecahedron  {1τ 0} Cube {100}
    Icosahedron {111}
    {    τ 1/τ 0}    		 Octahedron {111}
    Rhomb-triacontahedron {100}
    {τ 1 1/τ}    		 Rhomb-dodecahedron {110}
    Pentakis-dodecahedron {1/τ 3 0}
    {τ2 1 2/τ}
    {τ+1/τ 2 1/τ}    		 Tetrakis-hexahedron {210}
    Triakis-icosahedron {τ+1/τ 1/τ2 0}
    {τ 2/τ 1}
    {2 1     1/τ2}    		 Triakis-octahedron {1 1  √2-1}
    Deltoidal hexecontahedron {1+1/τ2 1 0}
    {τ2 1/τ 1/τ}
    {2 1 τ}     		Deltoidal icositetrahedron {1 1  √2+1} 
    Hexakis-icosahedron {2+τ2 1/τ 1/τ}
    {τ2 1 2/τ2}
    {2+1/τ2 τ 1/τ2}
     {2 3/τ 1}
     {τ+1/τ  2/τ  1+1/τ2}    		 Hexakis-octahedron
      {2√2+1  √2+1 1}
    Table 1

    Each set of indices relative to the icosahedral forms corresponds to a different form in the 2/m 3 cubic point group, subgroup of the 2/m 3 5 icosahedral point group.
    Concerning the Catalan deltoid-hexecontahedron (made of 60 faces), the three forms belonging to the 2/m 3 cubic point group in which it can be decomposed are, as shown in Figure 1:
  • the pentagon dodecahedron {1+1/τ2 1 0} (12 faces)
  • the deltoid-icositetrahedron {τ2 1/τ 1/τ} (24 faces)
  • the diploid {2 1 τ} (24 faces)

    • In the Catalan deltoid-hexecontahedron these pentagon-dodecahedral, deltoid-icositetrahedral and diploidal faces are related by the 5-fold axes.

    Decomposition of the Catalan deltoid-hexecontahedron in three forms belonging to the 2/m 3 point group: a pentagon-dodecahedron, a deltoid-icositetrahedron and a diploid

    pentagon-dodecahedron
    {1+1/τ2 1 0}

    deltoid-icositetrahedron
    {τ    2 1/τ 1/τ}

    diploid
    {2 1 τ}

    Catalan deltoid-hexecontahedron resulting from the intersection of the three single forms belonging to the 2/m 3 point group
    Figure 1

    In turn, the five forms (all made of 24 faces), in which the Catalan hexakis-icosahedron (made of 120 faces) can be decomposed, are, as shown in Figure 2:
  • the deltoid-icositetrahedron {2+τ2 1/τ 1/τ} (or {4τ+1 1 1})
  • the four diploids: {τ2 1 2/τ2}, {τ+1/τ 2/τ 1+1/τ2}, {2 3/τ 1}, {2+1/τ2 τ 1/τ2}

    • Obviously also in the Catalan hexakis-icosahedron these deltoid-icositetrahedral and diploidal faces are related by the 5-fold axes.
     

    Decomposition of the Catalan hexakis-icosahedron in five forms belonging to the 2/m 3 point group: a deltoid-icositetrahedron and four diploids
    deltoid icosi-tetrahedron
    {2+τ2 1/τ  1/τ}     		diploid
    {τ2 1 2/τ2}    		 diploid
     {τ+1/τ  2/τ  1+1/τ2}
    diploid 
    {2 3/τ 1}    		 diploid
    {2+1/τ2 τ 1/τ2}

    Catalan hexakis-icosahedron resulting from the intersection of the five forms belonging to the 2/m 3 point group
    Figure 2

    As shown in Figure 3, square faces of rhomb-triacontahedron can be generated only from its intersection with a deltoid-execontahedron {hk0} whose ratio h/k, included in the range: 1/τ < h/k < τ2, assumes the value h/k = 1+1/τ2 characterizing the (1+1/τ2 1 0) face of the Catalan deltoid-execontahedron (central image of Figure 3). In fact, the (1+1/τ2 1 0) face is the only (hk0) face that, by the action of the [τ 1/τ 0] 3-fold axis, becomes the (τ2 1/τ 1/τ) face, that is a (hkk) face: the (100) square face of rhomb-triacontahedron can be generated uniquely by the intersection just with (hkk) faces (when the relative h/k ratio is equal or greater than τ3). It follows from the orthogonality of the [011] and [0 1 1] directions, parallel to the edges between the (100) face and the contiguous (hkk) and (hkk) faces, becoming (τ2 1/τ 1/τ) and (τ2 1/τ -1/τ) in case of the Catalan deltoid-hexecontahedron.

    Intersection of the rhomb-triacontahedron with different deltoid-hexecontahedra: square faces can originate only in case of the Catalan deltoid-hexecontahedron
    Rhomb-triacontahedron {100}
    Deltoid-hexecontahedron {320}    		 Rhomb-triacontahedron {100}
    Deltoid-hexecontahedron {1+1/τ2 1 0}    		 Rhomb-triacontahedron {100}
    Deltoid-hexecontahedron {540}

    The intersecting rhomb-triacontahedron and deltoid-hexecontahedron in each image of the upper row are equidistant from the center of the polyhedron, whereas the rhomb-triacontahedron and the deltoid-hexecontahedron in each image of the lower row share vertices  as a consequence of an appropriate ratio of their central distances.
    The images of the central column show that square faces can originate only in case of the intersection of the rhomb-triacontahedron with the Catalan deltoid-hexecontahedron    .
    Figure 3

    Whereas the intersection with {hkk} forms characterized by a ratio h/k ≥ τ3 always generates square faces of rhomb-triacontahedron, generally square faces cannot be generated when the intersection with the rhomb-triacontahedron concerns faces belonging to {hkk} forms, usually hexakis-icosahedra, characterized by a ratio h/k <τ3.
    In such a case, the (hkk) "deltoid-icositetrahedral" face of the hexakis-icosahedron (see Fig.1), whose h/k ratio is included in the range 1<h/k <τ3, does not intersect the (100) face of the rhomb-triacontahedron and the same thing happens, when h/k < 1, with the "triakis-octahedral" face of the hexakis-icosahedron.
    The faces that, being the nearest to the (100) face of the rhomb-triacontahedron, intersect it, usually are instead four {hkl} "diploidal" faces of the hexakis-icosahedron, derived from the (hkk) face by the action of the symmetry operators. The indices of one of these {hkl} faces are reported, together with the {hkk} indices, in the captions of the sequence of images shown in Figure 4, ordered in columns according to decreasing value of h/k, starting from the deltoid-hexecontahedron {τ311}, whose intersection with the rhomb-triacontahedron generates square faces.
    However, as shown in the fifth row of the sequence, one can obtain square (100) faces, even if the ratio h/k is less than τ3, starting from both {1+2/τ2 1 1} and {1+1/τ2 τ2 τ2} hexakis-icosahedra. In fact, such hexakis-icosahedra include, by the action of the symmetry operators, also the "deltoid-icositetrahedral" faces with indices (1+τ2 1/τ2 1/τ2) and (2+1/τ2 1/τ2 1/τ2), respectively, where the value of the ratio h/k is greater than τ3; therefore, in both cases, the result of their intersection with the (100) face of the rhomb-triacontahedron is a face having a square shape.
    Then, according to the 2/m 3 point group, the five forms in which the former of these two hexakis-icosahedra can be decomposed are  three diploids and the two deltoid-icositetrahedra {1+2/τ2 1 1} and {1+τ2 1/τ2 1/τ2}, whereas the latter can originate three diploids, the deltoid-icositetrahedron {2+1/τ2 1/τ2 1/τ2} and the triakis-octahedron {1+1/τ2 τ2 τ2}. On the other hand, as already pointed out in Fig.2, the Catalan hexakis-icosahedra can be decomposed in a deltoid-icositetrahedron and four diploids, and, finally, five diploids can be derived from the generic hexakis-icosahedra.

    Resuming, as one can see in Fig.4, the {hkk} forms are all hexakis-icosahedra, excluding five forms:
  • the deltoid-hexecontahedra {τ311} and {011}, shown in the 1st row; whereas four "deltoid-icositetrahedral" {τ311} faces intersect directly the (100) face generating a square face, the deltoid-hexecontahedron {011} intersects the (100) face by means of four (τ2 1/τ2 1) "diploidal" faces: the result is a rhombic face instead of a square face
  • the pentakis-dodecahedra {τ+1/τ 1 1} and {1/τ3 1 1}, intersecting the (100) face by their "pentagon-dodecahedral faces": (τ4 0 1) and (τ4 0 1) in the first case, (1+τ2 0 1) and (1+τ2 0 1) in the second case (3rd row); the common result is a face of rhomb-triacontahedron having the shape of non-regular but symmetric hexagons
  • the icosahedron {111}, intersecting the (100) face of the rhomb-triacontahedron by the faces (τ 1/τ 0) and (τ -1/τ 0); also in this case the faces of rhomb-triacontahedron have the shape of non-regular but symmetric hexagons; they are orientated orthogonally to the previous hexagonal faces of  rhomb-triacontahedron, generated by the intersection with pentakis-dodecahedra.
     
    • The couples of composite forms reported in the six intermediate rows of Fig.4 are similar, even though they correspond to {hkk} forms characterized by values of the ratio h/k greater (left column) or less (right column) than 1.
    The faces of the couple of rhomb-triacontahedra in the 6th row, generated by the intersection with the hexakis-icosahedra {τ 1 1} and {1/τ 1 1}, have a rhombic shape, characterized by a ratio of the diagonals equal to τ.

    Intersections of the rhomb-triacontahedron with {hkk} forms in which the ratio h/k assumes decreasing values in the interval: τ3 ≥ h/k ≥ 0

    a) (100) face of the rhomb-triacontahedron intersected by the (τ311) face of the deltoid-hexecontahedron with the same indices

    o) (100) face of the rhomb-triacontahedron intersected by the (τ2 1/τ2 1) face of the deltoid-hexecontahedron {011} 

    b) (100) face of the rhomb-triacontahedron  intersected by the (3τ+1 1/τ2 1) face of the hexakis-icosahedron {τ211} 

    n) (100) face of the rhomb-triacontahedron intersected by the (5τ-1 1/τ2 τ+1/τ) face of the hexakis-icosahedron {1/τ4 11} 

    c) (100) face of the rhomb-triacontahedron  intersected by the (τ4 01) face of the pentakis-dodecahedron {τ+1/τ 1 1} 

    m) (100) face of the rhomb-triacontahedron intersected by the (1+τ2  0 1) face of the pentakis-dodecahedron {1/τ3 1 1} 

    d) (100) face of the rhomb-triacontahedron  intersected by the (3τ2 1/τ2 1) face of the hexakis-icosahedron {211} 

    l) (100) face of the rhomb-triacontahedron intersected by the (2+τ2 1/τ2 1) face of the hexakis-icosahedron {1/τ2 11} 

    e) (100) square face of rhomb-triacontahedron resulting from the intersection with the (1+τ2 1/τ2 1/τ2) face of the hexakis-icosahedron {1+2/τ2  1  1}

    k) (100) square face of rhomb-triacontahedron resulting from the intersection with the (2+1/τ2 1/τ2 1/τ2) face of the hexakis-icosahedron {1+1/τ2 τ2 τ2}

    f) (100) face of the rhomb-triacontahedron  intersected by the (τ3 1/τ 1/τ2) face of the hexakis-icosahedron {τ 1 1} 

    j) (100) face of the rhomb-triacontahedron intersected by the (3 1/τ 1/τ2) face of the hexakis-icosahedron {1/τ 1 1} 

    g) (100) face of the rhomb-triacontahedron intersected by the (7τ+5 τ+2 1) face of the hexakis-icosahedron {1+1/τ2 1 1} 

    i) (100) face of the rhomb-triacontahedron intersected by the (τ5 3τ-2 1) face of the hexakis-icosahedron {1 1+1/τ2 1+1/τ2} 

    h) (100) face of the rhomb-triacontahedron  intersected by the (τ 1/τ 0) face of the icosahedron {111} 

    Figure 4

    The animated sequence shown in Figure 5 reports the views along the [001] direction and the corresponding stereographic projections relative to twenty-five composite forms obtained from the intersection of the rhomb-triacontahedron with forms that include {hkk} faces, indicated by a red circle in the stereographic net, in which the ratio h/k varies in the interval 4τ+1 ≥ h/k ≥ 0 (the ratio h/k = 4τ+1 in a {hkk} form corresponds to the Catalan hexakis-icosahedron).

    Figure 5

    REFERENCES and LINKS
    1. International Union of Crystallography
       International Tables for Crystallography, Vol. A, Theo Hahn Editor, Kluwer Academic Publisher, 1989
    2. Zefiro L., Ardigo' M.R.
      Description of the Forms Belonging to the 235 and m35 Icosahedral Point Groups Starting from the Pairs of Dual Polyhedra: Icosahedron-Dodecahedron and Archimedean Polyhedra-Catalan Polyhedra
      VisMath, volume 9, No. 4, 2007
    3. Zefiro L., Ardigo' M.R.
      Platonic and Catalan Polyhedra as Archetypes of Forms Belonging to the Cubic and Icosahedral Systems
      VisMath, volume 11, No. 2, 2009