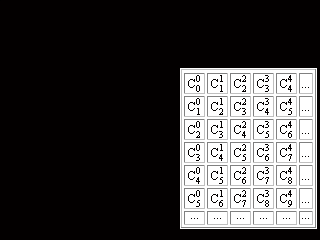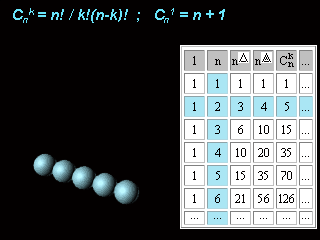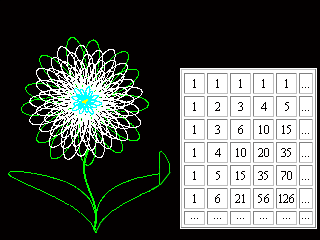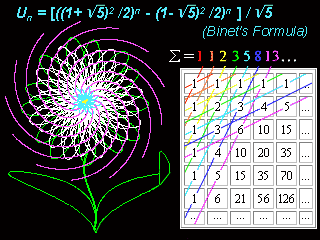
Figure 1. Pascal's Triangle, though named after Blaise Pascal, appears as early as the tenth century in Chinese mathematical scripts and probably is even older.
The Pythagorean Approach to Problems of Periodicity
in
Chemistry and Nuclear Physics
D. Weise
Key words:
The periodic law, the packing nuclear model, magic numbers, figurate numbers, Pascal's Triangle.
Periodicity of atom properties
Figurate numbers
Numbers, known as figurate or polygonal numbers, appeared in 15th-century arithmetic books and were probably known to the ancient Chinese; but they were of especial interest to the ancient Greek mathematicians. To the Pythagoreans (c. 500 BC), numbers were of paramount significance; everything could be explained by numbers, and numbers were invested with specific characteristics and personalities. Among other properties of numbers, the Pythagoreans recognized that numbers had "shapes."(Britannica)
Figure 1. Pascal's Triangle, though named after Blaise Pascal, appears as early as the tenth century in Chinese mathematical scripts and probably is even older.
Cnk = n! / (k! (n - k)!)
This is the same as the (n, k) binomial coefficient.
In columns and rows of the table starting from the second row we can find:
natural numbers (n = Cn1 = n,),
figurate:
triangular
(n
= Cn2=
(n2 + n)/2 ) numbers, and
tetrahedral
(n
= Cn3=
(n3 + 3n2 + 2n)/6) numbers.
(The
signs , , 
, 
,
et
cetera, used
in this work for designation of figurate numbers are not common).
The sequence of Fibonacci numbers, 1, 1, 2, 3, 5, 8, 13, . . . , in which each successive number is equal to the sum of the two preceding numbers.
If we replace ones in the first column with twos and build the 2nd, and 3th columns according to the fundamental rule, we will see:
odd
numbers (n
= 2n - 1)
- (the sign
is chosen because of its similarity to the gnomon of square),
square
numbers (n
= n2).
Let's move apart lines of the table and in the third column above each square let's write the same square. The fourth column (E) will be filled according to the of Pascal's Triangle rule (1, 4+1=5, 4+5=9, 9+9=18, 9+18=27 and so on). In the fifth column let's enter double numbers of the fourth column (2E).
It is necessary to notice, that in the fourth column the numbers of electronic pairs of atoms of inert, or noble, gases are written. In the fifth column, accordingly, - there are charges of these atoms, or magic numbers for atom.
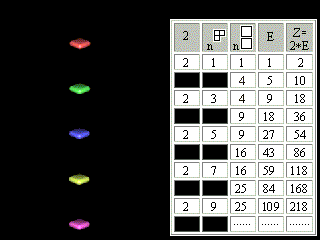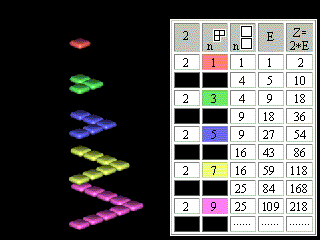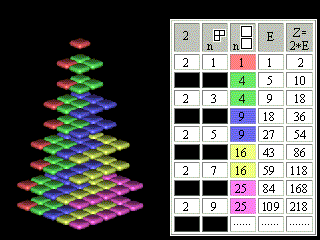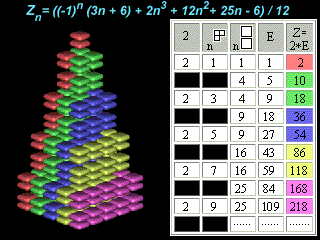
Figure 2. The modification of Pascal's Triangle
So, we have a 3D model of Mendeleyev's periodic system, to which it is possible to give the following explanations:
Figure 3. 3D Mendeleyev's periodic system
1. Periods.
A period corresponds to a horizontal layer of the submitted animation. Thickness of each period makes 2 building-blocks.
The amount of building-blocks in such a twofold layer corresponds to the amount of elements in the period and to the Principle Quantum Number N.
The top stratum withthe thickness of 1building-block in each layer corresponds generally to elements with uncoupled electrons. The bottom stratum corresponds to elements, for which coupled electrons are available.
Two monochromatic building-blocks posed one above another in every layer correspond to one electron orbital.
2. Electron subshells.
The elements, the properties of which are determined by outside electron subshells s, p, d, f, g, are grouped together in modules of individual colour.
s - red;
p - green;
d - dark blue;
f - yellow;
g (theoretically predicted) - lilac.
Outcome
of the analytical approach to mathematical singularities of the periodic
law of elements
The figurate-numerical approach allows for the expression of inert gases atoms charges by the algebraic equation:
Z = [ (-1)n (3n + 6) + 2n3 + 12n2 + 25n - 6 ] / 12
n = 1, 2, 3, ... (period number)
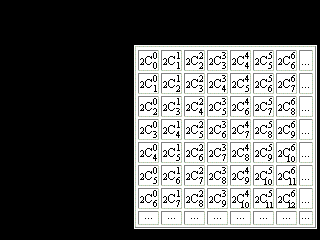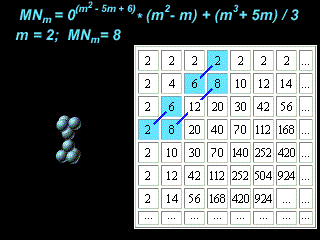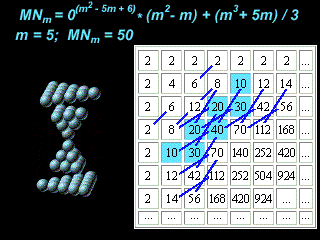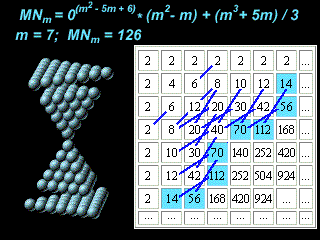
Figure 4. Another modification of the Pascal's Triangle. The values of all numbers in the table correspond to doubled numbers of the conventional Pascal’s Triangle.
Oblong
plane numbers n
= 2n
= n2
+ n ;
oblong
pyramidal numbers n
= 2n
= (n3+3n2+2n)/3.
The amount of spheres changing each other, is equal to magic numbers 2, 8, 20, 28, 50, 82, 126. The segments of dark blue lines bridge the numbers, which sum is equal to the next magic number. Symmetry and regularity of the marked numbers arrangement in the table attract attention.
The lowest values 2, 8, and 20 agree with independent nucleon motion into a single particle potential, like a harmonic oscillator.
MNm= (m3 + 3m2 + 2m)/3
m = 1, 2, 3.
The figures for numbers 28, 50, 82, and 126 agree, in addition to the central potential, witha strong spin-orbit coupling ( by Maria Mayer and Jensen) have the another form.
They are featured by the formula:
MNm= (m3+5m)/3
m = 1, 4, 5, 6, 7 ...
The combined formula is:
MNm= 0(m^2 - 5m + 6) * (m2 - m) + (m3 + 5m)/3
m = 1, 2, 3 ...
Author was surprised and pleased to have found similar
diagrams
and formulas on several pages of Linus Pauling's notebooks
(for example, the images 102, 174, 181, 185, 207, 218, 229, 230, 233).
References:
1. The Encyclopedia "Britannica" on CD 2000 Delux Edition & WWW pages.
2. Linus Pauling. Research
Notebooks
http://osulibrary.orst.edu/specialcollections/rnb/index.html
Research Notebook 25.
3. http://www.isis-s.unsw.edu.au/interact/gallery/image_files/wiese/weise.html