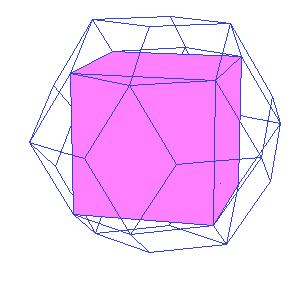
Dissection of concave triacontahedron



Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

In [2] we observed a certain dissection of rhombic triacontahedron. In [6] a certain tilling of space using rhombic triacontahedron and and a concav rhombic triacontahedron was studied.

Dissection of the concav triacontahedron, simmilar to that of the triacontahedron is also possible. The cube in the centre has edge length equal the smaller diagonal of the golden rhombus. We also need six halves of rhombic dodecahedron of the second kind.

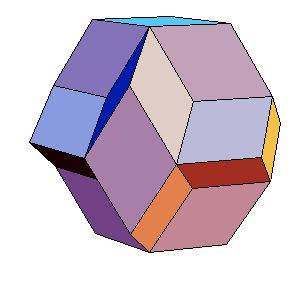
The half of rhombic consists of three triangular prisms.

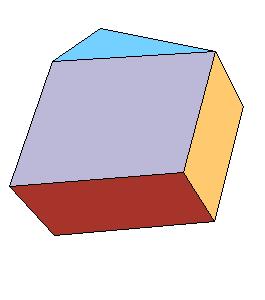
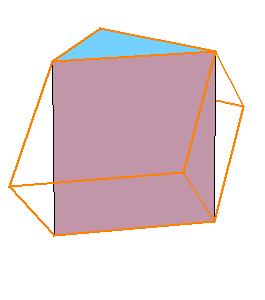
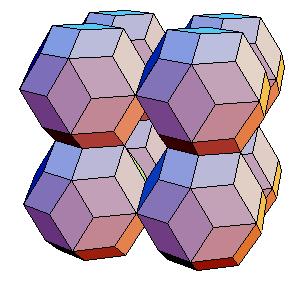
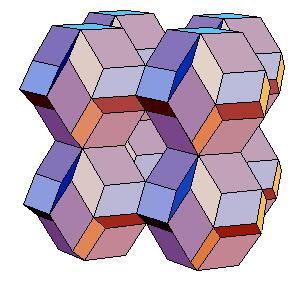
This gives as a new dissection of the triacontahedron, namely to 8 oblate rhombohedra, 6 halves of rhombic dodecahedron of the second kind, and a cube.

References


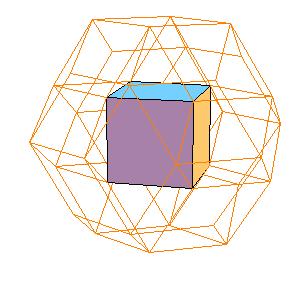
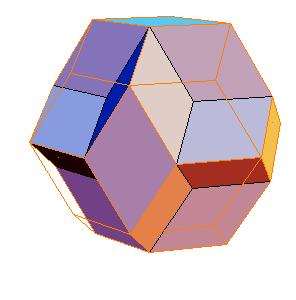
[1] I. Hafner, T. Zitko: From dissection of the cube to space filling with prolate rhombohedra and rhombic dodecahedra of the second kind - published in Visual Mathematics Vol.4, No.2, 2002, (5)
[2] A dissection of rhombic triacontahedron - published in Visual Mathematics Vol.8, No.3, 2006, (3)
[3] A dissection of two rhombic dodecahedra of the second kind to a cube - published in Visual Mathematics Vol.8, No.3, 2006, (1)
[4] A dissection of quarter of rhombic dodecahedron of the second kind to a cube - published in Visual Mathematics Vol.8, No.3, 2006, (2)
[5] http://torina.fe.uni-lj.si/~izidor/RhombicPolyhedra/RhombicPolyhedra.html
[6] R. Williams, The Geometrical Foundation of Natural Structure, Dover Publication, Inc, New York, 1972