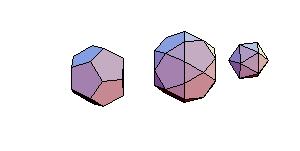
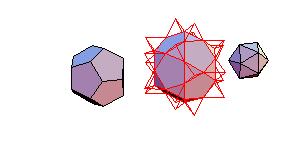
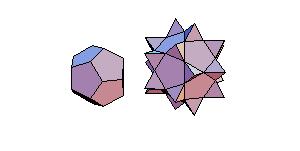
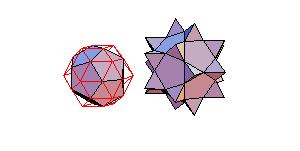
Animated Proof of Conway-Radin-Sadun Problem
Izidor Hafner
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25, 1000 Ljubljana, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
In [2] J. H. Conway, C. Radin and L. Sadun applied their theory of geodetic angles to the non-snub
Archimedean polyhedra proving that some combinations of Platonic and Archimedean solids
can be decomposed to a cube. In particular it was proved that it was possible to dissect
the icosahedron, dodecahedron, and icosidodecahedron into finitely many pieces that can be
reassembled to form a large cube. The problem is, how to perform such dissection.
Observe that there is an algorithm to dissect any number of prisms to a single cube [1, pg. 126].
Animations use Martin Kraus' Live3D applet [3].
References
[1] V.G. Boltjanskii, Tretja problema Hilberta, Nauka, Moskva 1977.
[2] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are rational,
Discrete & Computational Geometry, 22 (1999), pages 321-332.
[3] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html