Additional reports on designs from my formative design studio have been requested for inclusion in VisMath. For an explanation of the "Programmed Design," see Visual Mathematics, 4), Volume 1, No. 2, 1999.

Through coloration, student Tung has made use of the same programmed network, to convey different imagery. Among factors to be considered in the application of color, there are, first, a system that addresses the imperative of programming, then, an economy of color, the clear differentiations of each triangular subdivision from all contiguous triangular subdivisions, aesthetic sensibilities, emotive toning, and harmonic unison.

In order to retain the differentiation of each triangle, it is topologically impossible to color the network’s tiling in only two colors; for some of the vertices of the network have five-way intersections. In search of a systematic application, the decision was made to color triangles according to their orientations. In all, there are eight differently oriented triangles. When eight bright hues were applied, the effect was crazy-quiltish; thus, a reductive system of four colors, in which each color occupies two orientations, was settled upon. Out of a potential of many, two variations with engaging, associative traits were imaged.
 
 

In the number of colors being reduced to four and in each color taking over two orientations, each color configures a group of triangles that is superposable (through 90° rotations) upon the other three color groups. The four colors, chosen for this variation of the programmed network, are a fully saturated red and a fully saturated green, a shade of red and a shade of green.

Consequent to the nature of the coloration scheme, the colors are distributed in such a way that each color projects, in relation to the other three colors, a different magnitude of dominance in each of the quadrants. A certain subtle darkening is induced over some parts and a subtle brightening over others. In effect, then, each quadrant betrays a faintly different blush.
 
 

In 1821, the Swiss Canton of Basel split into two half cantons: Basel-Stadt and Basel-Land. The two crosiers of the original canon’s heraldic coat of arms, one plain and one studded, were accordingly divvyed between the two cantons—the plain crosier went to Basel-Stadt; the studded crosier, to Basel-Land.

The same network, lodged in the Poinsettia (Variation 1), accommodates the Two Crosiers (Variation 2). In the rendering of the network in this version though, four spiral arms are brought out: two in somber shades, two in sprightly tints.

In programming a dilatative assembling of the design’s elementary motif (illustrated below) there occurs a bit of overlappage of the building-block components. In the fourfold duplication of the generation of the initial spiral arm, certain sub-parts are noticed to belong to both contiguous spirals at once. The designer, then, had to choose to which spiral arms these dual claims would be assigned. However he chose, he could get but two studded spirals with smooth undersides, and two plain spiral with notched undersides.

While eight colors in all are used (a tint of red and a tint of green, a shade of red and a shade of green, and four gradations of grey), only four colors are used in each pair of spiral arms. The two studded crosiers are colored with the shades of red and green and the two darkest gradations of grey, with each color engaging two orientations; the two plain crosiers are colored with the tints of red and green and the two lightest gradations of grey, with each color again engaging two orientations.

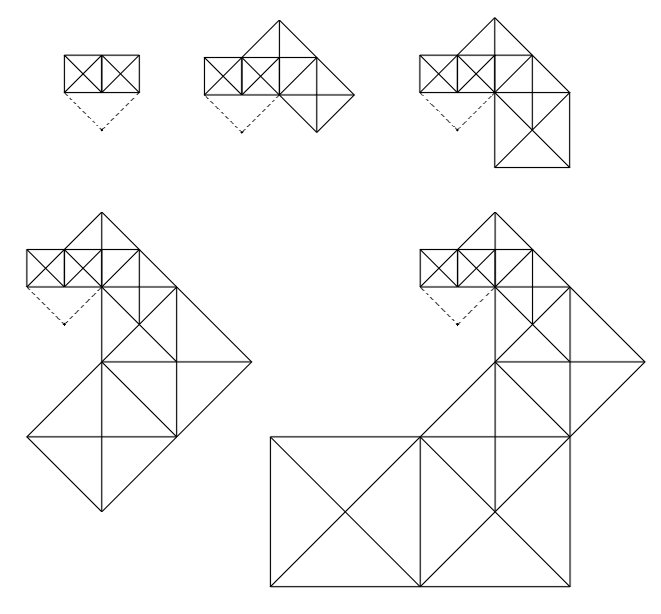
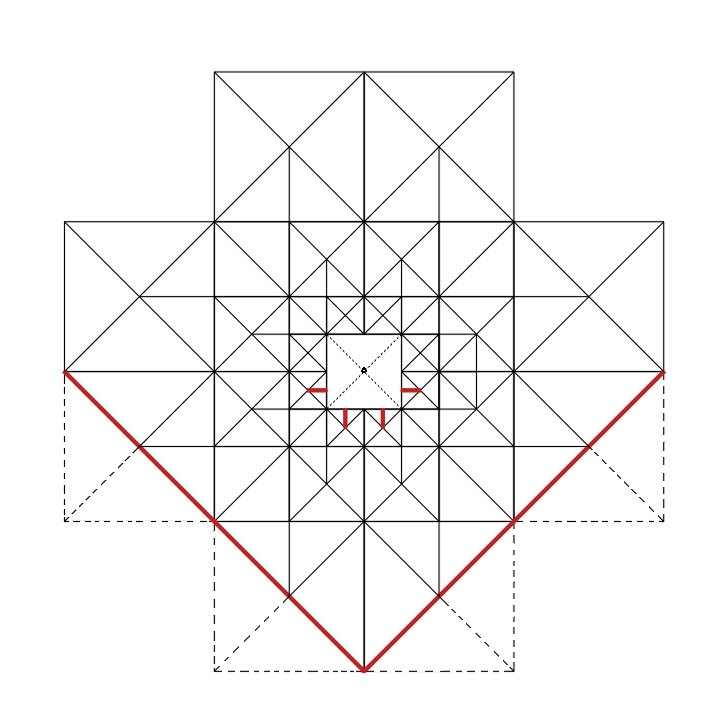
The basic structure of these two designs is a network of traianglar tiles that are framed within a square diamond. What may on the surface appear to be obvious is, yet, a devilishly difficult program to decipher and, thus, to reconstitute from point zero, partly because of is the instances of overlappage, which contribute to the design’s special properties.

The elementary motif is a pair of squares that share a common edge; both are diagonally crisscrossed. The diagonal (upward left to downward right) of the square to the right becomes the base of the first of two similarly crisscrossed pair of squares. One after another similar, crisscrossed, paired squares are grafted in the same fashion, so that a geometricly enlarging sequence of the parts develops into a spiral configuration. In each paired set of squares the criss of the left square and the cross of the right square form a 45° right triangle whose hypotenuse is the bases of the two squares.

A square diamond is defined (see dotted lines) by mirroring across the hypotenuse of the above described right triangle. The fourth vertex of this diamond falls outside the elementary motif, and this vertex pinpoints the origin of dilatation of the spiraling arm. When the spiral arm has been dilatated outwardly (and inwardly) to the designer’s satisfaction, the origin of dilatation seconds as a center of rotation; and by executing a fourfold operation on the spiraling arm, the whole network is accordingly configured. (The first step of grafting a second pair of crisscrossed squares onto the original pair of squares, could have been developed upon the first square at the left instead on the second one to the right—but the final configuration would have been the same.)

There are two modifications of the program—indicated by the red lines on one-half of the final shape of the network as its program was stringently executed: 
     (1) an outer diamond border is drawn along lines that already exist; 
     (2) a line in each of the eight innermost triangles that surround the central inner square space is added to match their similar counterparts where such lines otherwise occur from the overlappage of motif being dilatatively grafted onto motif; for the innermost pair of crisscrossed squares, even when the operative rules dilatate inwardly, will not receive these lines, short of the intervention of making this exception to the rules of the program. A purist might have resolved both issues in a different manner, but the license to resolve it this way was left to student Tung.