|
VISUALIZATION
OF THE REACTION ZONE SPREADING
Liljana
Stefanovska Faculty
of Technology and Metallurgy, P.O. Box 580, Skopje, Macedonia Toma
Grcev Faculty
of Technology and Metallurgy, P.O. Box 580, Skopje, Macedonia Sonja
Gegovska-Zajkova Faculty
of Electrical Engineering, P.O. Box 574, Skopje, Macedonia szajkova@cerera.etf.ukim.edu.mk ABSTRACT. Redox reactions between small solid particles (Me1/Me2
– oxide) are very fast exothermic and autocatalytical reactions, which take
place at the solid/liquid interface. An attempt to correlate the experimentally
obtained data for the alumothermic (Al/Fe3O4) reaction
with several mathematical
(geometrical) models for reaction zone spreading was made in this paper. INTRODUCTION
The processes in the redox systems, such as Me1/Me2 oxides, are basically very fast and they produce a large quantity of heat, which means that they are very high-temperature reactions. Besides we should say that these redox processes start in a solid phase (mixture of small particles of a specific metal oxide and the metal particles of the reducence) after the initiation of the reaction, the reaction continues to take place at the liquid/solid interface, during which, the new created liquid phase gravitationally falls down (moves) to the bottom of the reaction vessel due to its greater density. One
of the most common redox reactions of this type is the alumothermic reaction (ATR),
where the role of an oxydance is taken over by iron oxides, such as Fe3O4,
and the role of reducance -
small particles of elementary alumina (Al). An
attempt to correlate the rate of the alumothermic redox reaction Al/Fe3O4
to the shape (cylinder or cone) and geometric parameters of the reaction vessel
is made in this study. This reaction starts with a central initiation of the
reaction mixture (small solid particles) by an electric spark and its
termination occurs in several seconds. EXPERIMENTAL
The
rate of the ATR (Al/Fe3O4) was tested in cylindrical and/or
conic ceramic vessels where the quantity of reaction mixture depends on the size
of the vessel. The available data in the known literature for this type of
reactions, as well as our preliminary investigations, pointed out the dominant
influence of the reaction vessel’s geometry and therefore its dimensions were
varied regarding the diameter and the high of the vessel. Meanwhile, it was
found that the time of the ATR completion, due to the very high rates of ATR
(ranged between 2 and 11 s), as well as the inability to stop the process in a
certain moment before the ending, the obtained results refer only to the
dependence of the total reaction time on the reaction vessel’s geometry. RESULTS AND DISCUSSION
A part of the obtained experimental results are shown on Figure 1.
Figure
1. It is obvious
that the time for finishing the reaction tr
is linearly dependent on the diameter of the reaction vessel (for a constant
high), as well as on the high of the vessel (at a constant diameter of the
vessel). Using the regress analysis, according to the method of smallest
squares, with a high coefficient of correlation (r > 0.98), these results can
be represented with a great accuracy by the following equations
D = b tr
- for constant height of the reaction vessel, and
H = b’tr
- for constant diameter of the reaction vessel. It should be
mentioned that b and b’ are rate constants for a horizontal or i.e. vertical spreading
of the reaction zone, respectively. The determined values of these constants
point out that the constant b is a
function of H (the height of the
reacting vessel), and the constant b’
is a function of D (the diameter of
the reaction vessel). On the other hand, it was shown that the determined values
for b are two to three times smaller
than those for b’, which points that
the rate of horizontal spreading of the reaction zone is significantly slower
than the vertical one and can be the rate determining step. Analysing to the obtained data, the following relations can be done:
The relation
(3) clearly points out that the spreading of the reaction zone (b/b’)
fairly good follows the geometry of the reaction vessel
(D/H). This type of dependence
is obtained for both cylindrical and conic types of vessels. On the other hand
this relation has considerably contributed in suggesting the most appropriate
mathematical model for developing the ATR. As it was previously mentioned, the rate of this specific type of redox reaction between small solid particles of the reactants depends mainly on the rate of the development of the reaction zone, determined mainly by the geometry of the reaction vessel and can be represented by the differential equation
where K
is a constant of proportionality or rate constant of ATR and A(t)
is a surface of the reaction zone in time t.
The supposed mathematical model should start from the most likely possible form
of the reaction zone, with a given geometry, which would in perspective give the
best match with the obtained experimental results. Besides, as the least likely
and border cases we choose so called piston and cylindrical model of spreading of
the reaction zone while the ATR is taking place. Once more we should mention
that ATR starts with a point-like, central, initiating of the reaction mixture
in the reaction vessel by an electric spark and it goes on auto catalytically
and very fast in the whole volume of the reaction vessel. The
piston model supposes that the
rate of the horizontal spreading of the reacting zone is much more greater than
the speed of vertical spreading of the same (vhor>>vvert ) so that the reaction zone
is spreading vertically by creating so called pistons by the height of the
reacting vessel. On the other hand that means that the rate of developing of the
ATR is a linear function of time, because in one time unit the same quantity of
the reaction mixture reacts. This means that the time for finishing the ATR
would depend only on the height of the reaction vessel, but not on its diameter. (place the cursor over the picture to see the animation) Differing from the piston model, the so called cylindrical model supposes a spreading of the reaction zone in a shape of concentric cylinders, while vhor << vvert where at the very initiating of ATR, a reaction zone in a shape of cylinder with a high of the reacting vessel and minimal diameter of (for an example) 1 mm is created. (place the cursor over the picture to see the animation) Further, as the reaction goes on, this kind of
created zone is spreading in horizontal direction till the moment when its
diameter reaches the diameter of the reaction vessel. That means that in this
case the rate of ATR would exponentially rise as it is going on, using more and
more reaction mixture. If we, in the both cases -
the
piston and the cylindrical model, suppose a spreading of the reacting zone in the consecutive
steps of 1 mm, than in the first case (piston model) the number of
steps that corresponds with the rate of ATR would be only a linear function of
the high of the reacting vessel, but not of the diameter of the reacting vessel
as well. In the case of cylindrical model, the number of steps i.e. the rate of
ATR would be only a function of the diameter of the reacting vessel, but not of
its high as well. Of course these border cases are slightly possible, because
our experimental results (Figure 1)
clearly point out that the rate of ATR depends both on the diameter and the high
of the reaction vessel. On the other hand, based on the experimentally obtained relation (3), a conical model for developing the ATR is supposed, while the reaction zone is spreading in a shape of concentric cones, and its ratio D/H is equal to the ratio of the reaction vessel (D/H)reaction
zone = (D/H)reaction
vessel.
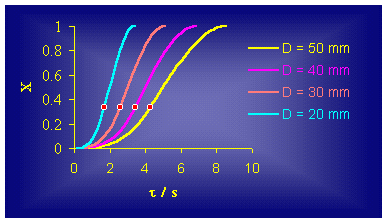
(5) (place the cursor over the picture to see the animation) Based on this model that starts from conic spreading of the reaction zone, kinetics of ATR, for several cylindrical vessels with constant high and variable diameter, can be obtained (Figure 2.), where x is a reaction degree (0 < x £ 1).
Figure 2. It is obvious that the obtained S - shape curves points out an existence of at least three phases (steps) in the ATR development. The first phase is initiation of the ATR, i.e. starting part of the curve whose lasting obviously depends on the diameter of the vessel and participates with an about 30% in the total time for ATR. The second, linear part, of these dependences is so called propagation, where the rate of the ATR is much greater. During this phase around 80% of the whole reaction mixture reacts, differing from the first, initial phase, when only 10% are reacting. The
third, final phase, a termination of the process takes place (the ATR fades).
Only around 10% of the whole reaction mixture reacts in this phase and after it,
the reaction degree x is
practically 1 (or 100%). As
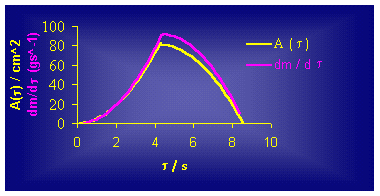
it can be seen from Figure 3., this model clearly confirms the concept that the
rate of ATR is a function of the reaction zone area, i.e. liquid/solid interface
(eq.(4)) Figure 3. According
to the conic model (Figure 3.), the reaction degree of 1/3 of the whole reacted
mass (x = 0.33) consumes 1/2 of the
total reaction time. That means that the total time for ATR in conic vessel,
with the same D and H
as in the cylinder, should be 50% shorter. This statement has been
confirmed by our additional results for both cylinder and cone reaction vessels.
Evidently, the point for which x =
0.333 is very closed to the inflection point (Figure
2.) of the obtained S -
type
curves. The experimentally obtained dependencies and the proposed model were analyzed using the equation x = 1
– exp (– K t n)
(6) i.e.
ln(– ln(1 – x)) = lnK + nln(nt).
(7) It was found
that the value of the reaction degree
K =
exp(1.84
– 0.25H – 0.94D)
(8) where H
and D are given in cm. Using the equations (6) and (8), accordance of around 95% regarding the experimental results for the kinetics of the ATR in cylindrical vessels is obtained. CONCLUSION
The
investigations of the very fast and auto catalytic high -
temperature
redox reaction in the Al/Fe3O4 system (in form of small
solid particles), which starts with central initiating by an electrical spark
and takes place at the liquid/solid interface, clearly pointed out that the rate
of this reaction mostly depends on the geometry of the reaction vessel. The proposed mathematical (geometrical) model for development of the ATR is based on the kinetic equation
supposing conic (central) spreading of the reaction zone, where (D/H)reaction zone = (D/H)reaction vessel is valid, gives an excellent fit with the obtained experimental results. On the other hand, an empirical equation, which correlates the reaction kinetics of the ATR with the geometric parameters of the reaction vessel, has been proposed in this study. The model we propose is an ideal one. In real case, the spreading of the reaction zone is in the shape of paraboloid shown in the following animation. (place the cursor over the picture to see the animation)
REFERENCES
[1]
Fur, Z. I., Zurnal fiziceskoi himii, T34, 1960, 611-17 [2]
Maksimov, E. I. at
all. Stal, 26(4), 329-30, 1966 [3]
Pliner, Á. L., Ignatenko, G. F., SB Trud Klincersk Zavoda Ferrosplavi, No 2, 22-26, 1965 [4] German, R. M., Ham, V. , Observations on the compaction of binary thermite power mixtures, Power. Technol. 1979, 22(2), 238-45 |
and it is practically independent of the geometry of the reaction vessel. On
the other side, the value of the reaction rate constant K
is a function of the diameter and the high of the reaction vessel, and the
following empirical dependence is obtained
