• geometrically on the harmonic series, in which every value multiplied by j provides the next value, i.e.:
  

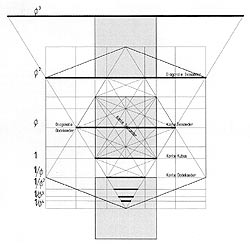
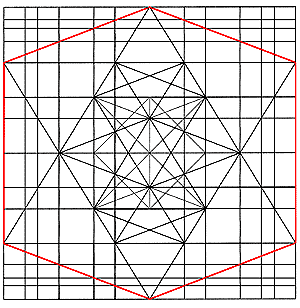
... 1/j³ : 1/j² : 1/j : 1 : j : j² : j³...

(In additive progression, each value is the sum of the two preceding ones. These properties produce an arithmetical and geometrical series at the same time.)

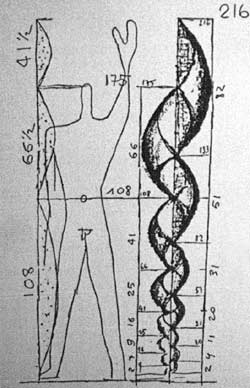
But it is also based on the additive Fibonacci number series, i.e.:

1 : 1 : 2 : 3 : 5 : 8 : 13 : 21 : 34 : 55 : 89 ...

in which each value is the sum of the two preceding ones, an approximation to the harmonic series, and thus tends rapidly to j, as shown by:

2 - 1,5 - 1,6 - 1,625 - 1,6154 - 1,619 - 1,6176 - 1,6181 - 1,6179 > j= 1,6180339

• abased on an introduction of the human scale, whereby Le Corbusier assumes the size of a human to be 1.83 m (almost exactly 6 feet), the other important body measurements and spatial dimensions being obtained from the j series such as
  
  

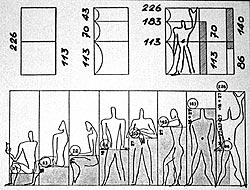
10 - 16 - 27 - 43 - 70 - 113 - 183 - 296 (red series)

and its doubling:

20 - 33 - 53 - 86 - 140 - 226 - 366 - 592 (blue series)

• exclusively on rectangularity.
  

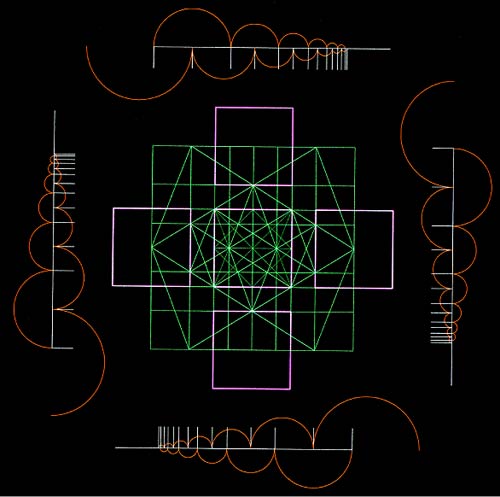
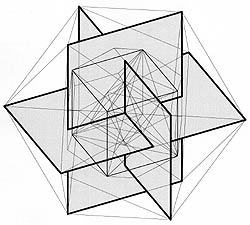
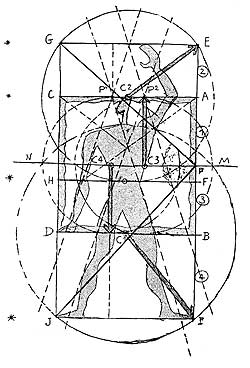
The harmonic series is contained in the Metaeder. The Modulor is situated on a.