It is possible to circumscribe each one of the Platonic or Archimedean bodies with a sphere or include a sphere within it.

The vertices of the solids touch the surface of the circumscribed sphere, the centre points of the polyhedron surfaces lie on the inner sphere.

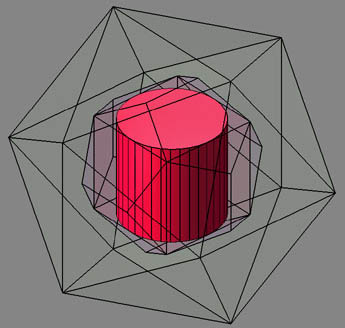
Cones can be circumscribed within the Metaeder, in our example as a double cone inside a cube.

Sectional planes through a cone produce:

• parallel to its base - a circle
  
• obliquely to its base - an ellipse
  
• parallel to its surface line - a parabola
  
• parallel to its axis - an hyperbola
  

SPHERES, CONES AND CYLINDERS IN METAEDER