HYPERBOLIC GEOMETRY
The founders of a "new geometry"are Gauss, Janos Bolyai and Nikolai Lobachevski for they were the first to deny the absolute nature of Euclidean geometry and provide us with a theory based on axiomatic methods.
What
remains to finish the story is a particular
realization of non Euclidean
geometry.
That
means a set of objects called "points", "lines"
and "planes" which are related in the way developed by Gauss,
Lobachevski and Bolyai.
The main problem in the visualization of the Hyperbolic plane is our lack of experience about it. We solve it using various models of the Hyperbolic plane. A model is an assignment of mathematical objects from Euclidean geometry to "play the role of" the non-Euclidean objects.
We visualize the
following models of the hyperbolic plane using our
package:
| POINCARE DISK |
| KLEIN DISK |
| POINCARE HALFPLANE |
Our Mathematica® package provides you with the possibility to choose between them.
Entire, infinite two-dimensional Hyperbolic Space is realized in the interior of the unit disk or in the upper halfplane, depending on the model. Boundary circle or the ordinate represent the infinity, so parallel are those lines whose intersection points lie in "infinity".
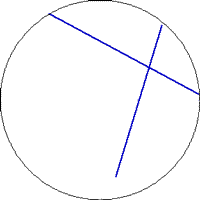 |
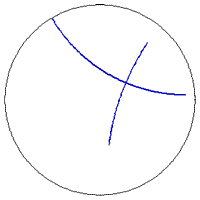 |
 |
The lines drawn in the models are not Euclidean lines. Moreover, their look depend on the model. Here is a table showing what are the lines in different models:
| MODEL |
KLEIN DISK
|
POINCARE DISK
|
POINCARE HALFPLANE
|
|
LINES
|
segments of
Euclidean lines inside of the unit disk |
arcs of Euclidean
circles
orthogonal to the boundary circle or diameters of the boundary circle |
arcs of Euclidean circles orthogonal to the x - axes or vertical rays |
The following picture shows a 'square" in these models; exactly the same polygon obtained from one by isomorphisms between models:

All pictures so far are produced using our package. It contains implementation of all basic objects - points, lines, polygons, circles...
Here is a same triangle triangle in all three models.
 |
 |
 |
|
Poincare Disk
|
Klein Disk
|
Poincare Halfplane
|
An important feature of our package is that it provides various motions (isometries) of the plane. The isometries are implemented as a compositions of symmetries and can be easily applied even to the most complicated objects. We start by rotation of our polygon around a given point:
 |
 |
 |
|
Poncare Disk
|
Klein Disk
|
Poincare Halfplane
|
Now, we reflect it with respect to a given line:
 |
 |
|
Poincare Disk
|
Klein Disk
|
"translate" it from one point to another:
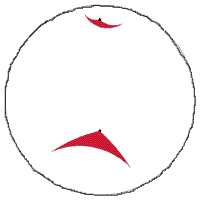 |
 |
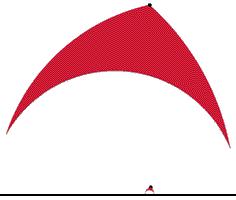 |
|
Poincare Disk
|
Klein Disk
|
Poincare Halfplane
|
And finally, rotate it around an infinite point - this isometry is called horocyclic rotation.
 |
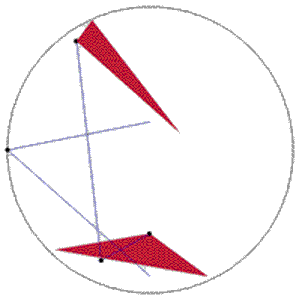 |
|
Poincare Disk
|
Klein Disk
|