|
and Escher’s Tiles
Abstract When the first cave-woman pressed an olive or nut, she got an oil that wouldn’t mix with water. Why? One reason is because the molecules’ shapes have different symmetries. In brief, an asymmetrical molecule is better able to form a dipole, which permits dipole-dipole intermolecular attractions [1]. So, chemical reality is
"somehow" related to mathematical symmetry. This by itself is exciting
to those interested in chemistry, but others may need more visual examples.
People who may feel intimidated by or bored with mathematical theories
of groups will be drawn in to the world of symmetry in architectural tiles
and in art using the ideas expressed in the art of M. C. Escher.
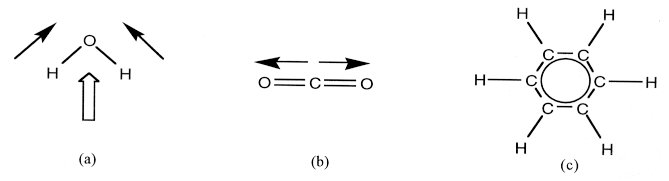
Symmetry and Chemistry In general, highly symmetrical molecules are hydrophobic ("water-fearing"), while hydrophilic molecules ("water-loving") have a unique direction, or polarity. For example, water (H–O–H or dihydrogen oxide) itself has a bent shape, so the electronic trends of its two O–H bonds can add together (figure 1a). In contrast, several non-polar, hydrophobic molecules have high symmetry. For example, O=C=O (carbon dioxide) is completely linear (Figure 1b). The net electronic trend is also zero in C6H6 (benzene), with its six equal C–H sections in a hexagon (Figure 1c). These trends all cancel exactly, because of the shape and symmetry of the molecule.
Figure 1. (a) The addition of electronic forces (thin arrow vectors)
from the O–H bonds in water permits
So, symmetry affects the polarity and
thus the solubility of substances. For related reasons, other properties
also are affected by symmetry, such as vapor pressure, melting point, boiling
point, crystal diffraction of x-rays or neutrons, spectroscopies
such as infrared, Raman, and nuclear magnetic resonance ("MRI" imaging).
With experience, chemists can see a harmony among the relationships of
these different properties of the world’s substances. However, even people
with no technical experience can appreciate and understand some of the
symmetry foundation of the universe through relevant art works.
Symmetry and Point Groups Many of the drawings of M. C. Escher demonstrate certain symmetry relationships [2]. One technique he used follows the method of tiling or tessellation, which has been used for centuries in different cultures. This is the regular filling of a surface with identical (monohedral) or related objects, leaving neither gaps nor overlaps. While molecules are three-dimensional objects, and tiling patterns are generally on a flat surface, it is possible to illustrate some symmetry relationships with tessellations. Artistic patterns can inspire and interest those who examine chemistry or mathematics, while less complex tilings with the same symmetries can clarify some relationships of molecules. For at least half a century, people have realized that tessellations demonstrate two-dimensional analogs of the three-dimensional symmetries of solid molecules, following the principles of crystallography [3,4,5]. The present work is not focused on the repetition of molecules in a crystal, but on the inherent symmetry of individual molecules, called point-group symmetry [6,7]. This molecular symmetry is often not used by crystals. Relationships are naturally indirect between non-repeating three-dimensional point-group symmetry and repetitive two-dimensional tessellation symmetry. The elements of point-group symmetry are
rotation, reflection, and inversion of all atoms in the molecule, in three
dimensions about a fixed central point, with no net change to the molecule.
In contrast, the elements of tessellation symmetry are rotation, reflection,
glide reflection, and translation of a side of a polygon to one other side,
to create a tile that can exactly cover the surface [8].
While these tessellation symmetries thus do not correspond to molecular
symmetries, they can suggest them, without requiring three dimensions.
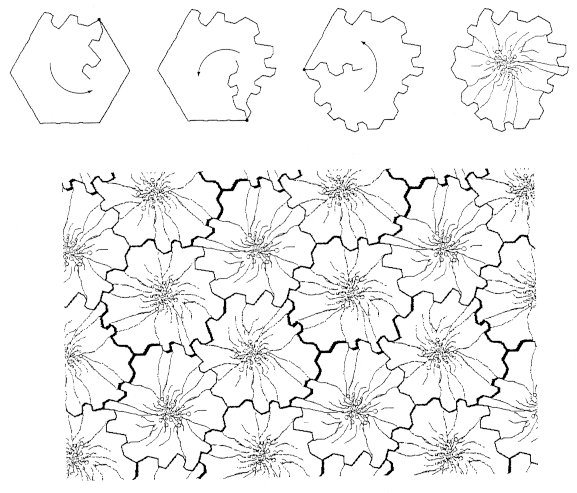
Symmetry Groups and Tessellation M. C. Escher wrote, in regard to regular tessellation, that "it is the richest source of inspiration that I have ever tapped, and it has by no means dried up yet." [12] Escher twice visited the Alhambra in Spain, and made several sketches of the tile designs found there. About this he wrote that "The Moors were masters in the filling of a surface with congruent figures and left no gaps over." There can be no doubt about the great significance of this art form to Escher, when he wrote that "Periodic drawings are . . . not subjective; they are objective. . . . For once one has crossed over the threshold of the early stages, this activity takes on more worth than any other form of decorative art" [12]. For two-dimensional tilings of a surface, there are 17 different plane symmetry groups, cataloged by the Hungarian mathematician G. Pólya in 1924 [9]. These can be categorized by asking questions as to the smallest symmetric rotation, and the presence of translation, reflections, and glide-reflections, and their relationships. These 17 symmetry groups yield 81 possible isohedral tiles [10]. Here, a tiling is isohedral if, "for every choice of two tiles in the tiling, there is an element in the symmetry group of the tiling that sends one of the tiles onto the other" [11]. The German mathematicians Heinrich Heesch and O. Kienzele later analyzed the types of asymmetric tiles that can form a tessellation without reflections (Table 1) [13]. This leaves seven of the 17 plane symmetry groups (called p1, p2, p3, p4, p6, pg, and pgg). From these, there are only 28 isohedral tile types.
Table 1. Heesch’s table of the 28 types of asymmetric isohedral tiles [13]. Each tile has 3 to 6 edges. Each edge has a symmetry relationship within itself or with another edge. Either one half of an edge coincides with its other half by a half-turn rotation (called C ), or one edge relates to a second edge, adjoining or across from it, by translation, rotation of order n (n>2), or glide reflection (called T, Cn, or Gn). For each tile, the shape can be thought of as a basic figure (square, triangle, quadrilateral, pentagon, or hexagon), combined with modifications or distortions of the edges, following the rules of its symmetry group. The translation (T ) operation means that, for example, a concave shape applied to one side of a square requires the same shape applied to the opposite side, now in a convex sense. Thus, translation conserves the area of the original rectangular or hexagonal figure (as do the other operations). A rotation symmetry edge, Cn, is the operation that copies a shape from one edge onto an adjoining edge, related by a pivoting on the common vertex by an angle of 2p/n. A glide-reflection, Gn, is also a translation to the opposite side of the figure, but one in which the shape of the edge is reflected across the line of translation. So, a bump out on the upper left becomes a bump in on the lower right. The Heesch symbol that categorizes a tile "is obtained by traveling a circuit around its boundary and associating to each edge the appropriate letter. Edges with a center of half-turn symmetry (C or C2) are related to themselves; other edges are related to an adjacent or to an opposite edge by a translation, glide-reflection, or rotation" [8]. Now that these symmetry categories have
been established, visual examples are needed to illustrate them. These
examples are chosen based on the symmetry of selected molecules (Table
2). Each of the representative molecules in Table 2 is planar, and represents
either a different point-group symmetry or chemical behavior, or both.
Table 2. Molecular and tessellation symmetries for selected planar molecule examples.
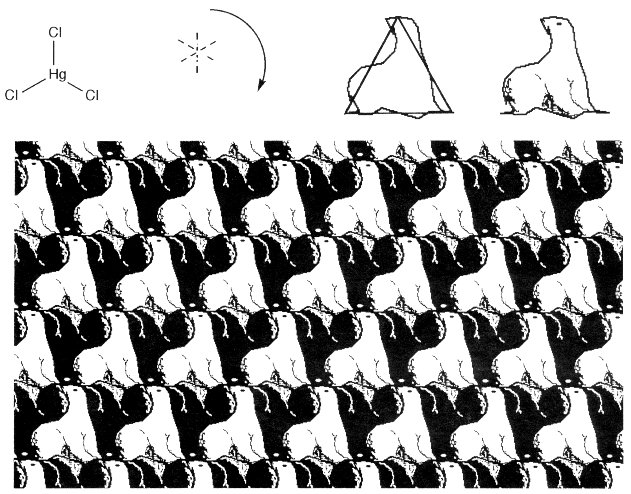
The table lists the Schoenflies three-dimensional point group symbol used by chemists, and a simplified three-dimensional international symbol used by crystallographers. The table also lists the two-dimensional international symbol of the tessellation group, and the specific tile symmetry under Heesch’s system, chosen by its analogy to three-dimensional symmetry, while avoiding reflection operations. These examples can now be illustrated, both with geometrical symbols, and with tessellation artwork. In this artwork, an individual shape has one or more sides modified according to Heesch’s applicable symmetry rules. The shape is given patterns or colors, then is replicated by again applying these rules of symmetry. Escher also developed and applied patterns of shading or color symmetry on many of his tessellations, which we do here for artistic purposes only. Some tessellations can be conveniently created with the aid of appropriate computer software [14]. The planar-triangular HgCl3- anion (point-group D3h) has three mirror planes and a rotation symmetry element of 2p/3 from each vertex (Cl) to the next. It also can be represented by a CCC tessellation figure (international symbol p2), where half of each side of an equilateral triangle has an arbitrary shape and can be rotated to the other half, under the C operation (Fig. 2).
Figure 2. Planar-triangular HgCl3- anion, and a related CCC tessellation.
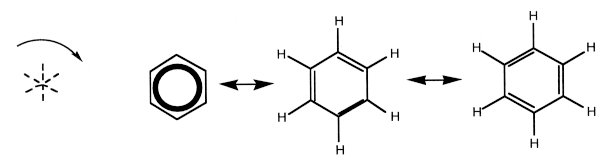
Benzene, C6H6, a discrete molecule with D6h point-group symmetry, has a 60º rotation center and 6 mirrors (3 shown, and their bisectors) in the benzene plane (Fig. 3).
Figure 3. Benzene, C6H6. Three different but equivalent representations of one benzene molecule are shown. Here, benzene is tessellated as a flower with a C3C3C3C3C3C3 form (international symbol p3), in Figure 4.
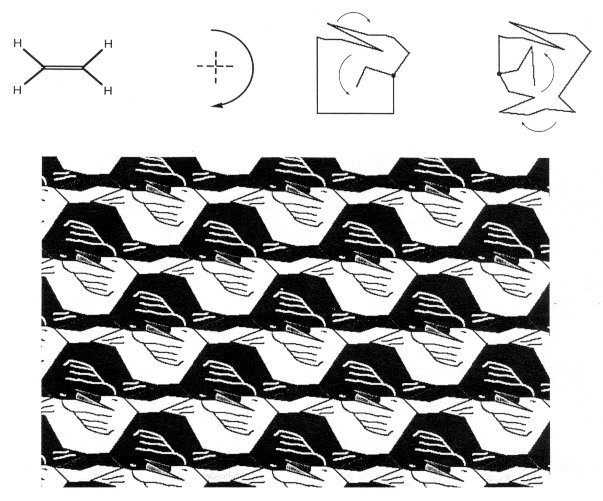
Figure 4. Benzene is tessellated as a C3C3C3C3C3C3 flower. Ethylene, H2C=CH2, is in point-group D2h (in mmm), and has two mirror planes and a 180º rotation axis. It can be tessellated as CCCC, for example as a duck (Fig. 5).
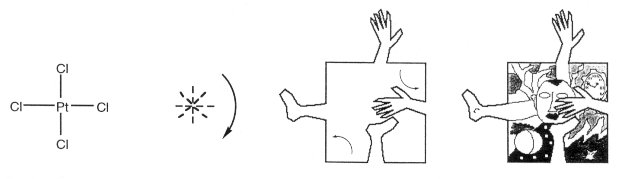
Figure 5. Ethylene can be tessellated as a CCCC duck. Tetrachloroplatinum, PtCl4, is in point-group
D4h (in 4/mmm), and has three mirror planes and a p/2
rotation axis. It can be tessellated as C4C4C4C4,
as was this image, a tribute to modern art (Fig. 6 and 7).
Figure 6. Tetrachloroplatinum can be represented
as a C4C4C4C4
figure.
Figure 7. A C4C4C4C4 figure is tessellated to show the symmetry of the PtCl4 molecule. These results serve simultaneously to
illustrate tessellation symmetries and three-dimensional molecular symmetries.
Some analogies are more obvious than others, and further examples are possible.
A future paper will discuss these in relation to the symmetries of frieze
border patterns.
References [2a] Visions of Symmetry: Notebooks, Periodic Drawings, and Related Work of M. C. Escher, Doris Schattschneider, W. H. Freeman and Co., New York, 1990. [2b] See also figures 8 and 9 in our other paper in these proceedings, Circles: A Paradigm for Paradox. [3] M. C. Escher’s brother, Beer, a teacher of crystallography, proposed in 1948 to write a book on this subject, with his brother illustrating [2]. Their project never materialized, though Escher later helped to produce such a work: Symmetry Aspects of M. C. Escher’s Periodic Drawings, Carolina H. MacGillavry, Utrecht: Oosthoek, 1965. Reprinted as Fantasy and Symmetry, 1976. [4] A key crystallography reference is International Tables for X-ray Crystallography, Vol. I, N. F. M. Henry and K. Lonsdale, eds., Kynoch Press, Birmingham, England, 1952. [5] G. H. Stout and L. H. Jensen, X-ray Structure Determination: A Practical Guide, Macmillan, 1968. [6] F. A. Cotton, Chemical Applications of Group Theory, 2nd ed., Wiley-Interscience, 1971. [7] F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry: A Comprehensive Text, 4th ed., Wiley Interscience, 1980. [8] Schattschneider, op. cit., pp. 323 - 328. [9] G. Pólya, Zeitschrift für Kristallographie, "Über die Analogie der Kristallsymmetrie in der Ebene," 1924, 60, 278-282, cited in [2a]. [10] B. Grünbaum, G. C. Shephard, Tilings and Patterns, W. H. Freeman, 1987, p. 288-90. [11] Schattschneider, op. cit., p. 323. [12] M. C. Escher, Regelmatige Vlakverdeling (Periodic Space-Filling), Utrecht, 1958, cited in B. Ernst, The Magic Mirror of M. C. Escher, J. E. Brigham, trans., Taschen, 1994, pp. 35-41. [13] H. Heesch and O. Kienzele, Flächenschluß, Springer-Verlag, 1963, cited in [2a] p. 326. [14] All tessellations herein were created by the authors or by Jill Etheridge with the program Tesslemania©, version 1.1 for Macintosh, Kevin D. Lee, Sandpiper Software Inc., ©MECC, Minnesota, 1994. |