The ultimate desire of mankind is to identify wholeness, to grasp the essence of being, to be integrated with the harmony, perfection, patterns, and cycles of the material, metaphorical and metaphysical worlds. This desire motivates us to explore the realms of fact and fancy, logic and metaphor, reason and emotion, to capture the whole of being in one part, to see it, hear it, feel it, and enjoy it in everyday life.

The circle is an object of nature, an idealization of pure mathematics, and a symbol or framework we use to understand and describe our world. The circle exists independently of human thought, as ripples in a pond, or the appearance of the sun and moon, or the shape of the iris of an eye. In mathematics, we choose to define a circle as the places at a constant distance from a center, usually in two dimensions. In this article, we look back at world history and the varied uses of the circle: literal and literary, physical and poetical, mathematical, metaphorical and mystical.
 
 

The circle crowned the head of the ancient Egyptians’ sun god, Ra. The Celtic Druids carved circular and spiral patterns in stone monuments. Their sacred places had a circle of large stones up to thirty yards in diameter, such as at Stonehenge. The Yin-Yang symbol of two parts spiraling within a circle is a traditional icon of Confucianism and Taoism (Figure 1). It suggests movement around the inside of the circle. It also provides a paradigm of polarity with which to view the dynamics of everyday life. As a symbol, it can be as personal and internal as a heart, which gives and receives blood through each complete cycle. It can also be as general and external as the cycles of day and night.
 

The Buddhist circular mandala designs have been used continuously for millennia (Figure 2). "A mandala (Sanskrit for "circle") is a symbolic diagram of the universe, arranged in circles, used in tantric Buddhism. The Swiss psychologist Carl Jung considered the mandala to be a universally occurring pattern associated with the mythological representation of the self [1a]."
 

Zoroastrianism, the tradition of ancient Persia, is believed by scholars to have been influential in the later development of metaphysical concepts in Abrahamic and Eastern religious beliefs [2a]. Its influence survives to our own day, not only in central Asia, but in such products of the European post-Romantic movement as Richard Strauss’s music and Friedrich Nietzsche’s book, Thus Spoke Zarathustra. Modern historians have dated the time of Zoroaster to approximately 1750 BC. Also known as Zarathustra, he was the founder of the Zoroastrian tradition [2b].

One symbol of Zoroastrianism is the Fra-vahar, a figure that stands for the ideal moral and spiritual focus in life (Figure 3). Fra is the direction, forward, and vahar describes a pulling force. Of the two circles in the figure, the ring in the hand is a reminder that we are bound to keep our promises or agreements with others. The other circle, at the waist, reminds us that our spirits live on, in essence immortal, and so also symbolizes infinity.

A series of coaxial circles is used on the Great Stupa temple at Sanchi, India, to indicate higher levels of being [3]. The Hindu cosmology included spheres as well as circles. The Navajo kiva or prayer room is circular, as are many mosques [4].

The circle has represented the divine, as well as the universe and groups of people in it [5]

                                         Isaiah said: "To whom then will ye liken God?
                                         or what likeness will ye compare unto him? ...
                                         Have ye not known? have ye not heard?
                                         hath it not been told you from the beginning?
                                         have ye not understood from the foundations of the earth?
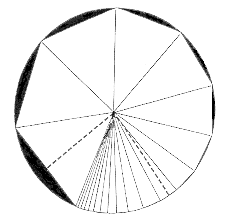
                                         It is he that sitteth upon the circle of the earth,
                                         and the inhabitants thereof are as grasshoppers; ..."
 
A saying derived from words attributed to Empedocles suggests the ancient Greeks may have also thought of these connections [6].
 
 

The Greeks tried to explain the world, from the mystical to the scientific. The Pythagoreans developed geometrical relations for much of the world around them, but found the apparently simple circle to be a serious challenge. The Babylonians, Egyptians, and Greeks recognized that the ratio of a circle’s circumference or periphery to its diameter was a constant, found to be about 3.14, which we call p (pi). The Pythagorean Greeks hoped to use geometry to relate the areas of the figures of a circle and a square, or "to square a circle" using a compass and straight edge.

Johann H. Lambert, the great eighteenth-century logician, was the first to demonstrate the irrationality of p. Beyond the classification of real numbers into rational and irrational numbers, the irrationals can also be classified as either algebraic or transcendental. A number is said to be algebraic if it can be the root of a finite polynomial equation with integer coefficients not all zero. A real number that is not algebraic is called transcendental. In 1882, the German mathematician Ferdinand Lindemann finally proved that p is a transcendental number. This settled the question of squaring the circle, since only algebraic dimensions can be constructed by using a compass and straight edge.

The Pythagoreans developed a method to represent the area of a circle by dividing it up into an infinite number of pie slices, which are essentially infinitely narrow triangles, as high as the circle’s radius (Figure 4) [7]. This gives the area by applying the simple formula for triangles. However, this converts the problem of the circle into the problem of infinity. Zeno confronted the Pythagoreans by asking if a slice of pie with a curved base can be represented with a flat-edged triangle before it is infinitely thin, and if the triangle is infinitely thin, then how can a real area be described by a collection of "nothing." The Greek search for mathematical rigor faced a daunting paradox.
 

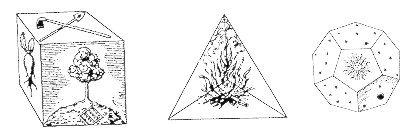
Different cultures throughout history have associated the square with the tangible world, and the circle with the perfect, ideal or the divine universe. The Pythagoreans and Plato associated the five regular Platonic solids with the four ancient elements of Empedocles, where earth is thought of as the cube, in the sense that one lives within one’s own four walls. Similarly, fire is the tetrahedron, and the almost-spherical dodecahedron represents the universe. This is illustrated in Figure 5, from Johannes Kepler’s Harmonices Mundi, Book II (1619) [8].

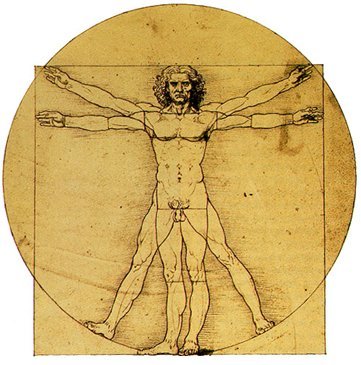
Perhaps because the circle couldn’t be squared mathematically, it was intriguing to do it visually. Leonardo DaVinci fit the proportions of the limbs of a human body into a circle and a square (Figure 6). Leonardo was illustrating the "ideal" proportions of human limbs relative to body size.