All kinds of art use geometry directly or indirectly. Even the most complicated painting composition may have a geometric structure in its basis. Sometimes, this structure is static, stable, based mostly on bilateral symmetry, but in many situations a rhythm of forms, lines and colors is an element or even the background of a whole structure. According to M. Ghyka [1], rhythm is observed and recorded periodicity. One of the simplest tools to suggest rhythm and contrast is the use of alternating black and white patterns. 

Periodical repetition is often used in decorative arts. A separated motif is static, but by repetition it imposes itself and creates a dynamic structure. Every periodical repetition suggests some kind of motion. We distinguish several types of periodic patterns:

1. Basic repeation (rotation, translation), suggesting oriented motion;
2. Alternation (glide reflection), producing stronger dynamic visual effect of double motion;
3. Inversion (convex-concave alternation);
4. Overlapping and interlacing (mostly alternating), which introduce a space component.

Alternatively, a very strong dynamic component may be introduced by coloring. Using contrast, complementary colors, "black-white", "light-dark", "over-under", "above-below", "positive-negative", "convex-concave", the same object can be turned into its opposite, increasing the rhythm and dynamics.

The idea of studying ornaments of different cultures from the point of view of the theory of symmetry originated with A. Speiser (1927) [2]. Among the early works in that field we can distinguish the analysis of Alhambra patterns given in the Ph.D. Thesis by E. Müller (1944) [3] and the papers of A. Shepard (1948) [4]. The very influential monograph "Symmetry" by H. Weyl [5] inspired the appearance of a whole series of works dedicated mostly to the ornamental art of ancient civilizations, to the cultures which contributed the most to the development of ornamental art (Egyptian, Arab, Moorish, etc.), and to ethnic ornamental art. Only in some recent works (e.g., by D.K. Washburn [6, 7]), and S. Jablan [8]) has research turned to the very roots, the origins of ornamental art - to the ornamental art of the Paleolithic and Neolithic, or to ethnic ornamental art. 

Thanks to the intensive development of the theory of symmetry and mathematical crystallography, the analysis of ornamental art completely followed this development. The more recent generalizations of the theory of symmetry, antisymmetry and colored symmetry are present in the graphic work of M.C. Escher [9, 10], as well as in several symmetry-related books and papers (e.g., in the books "Symmetry in Science and Art" by A.V. Shubnikov & V.A. Koptsik [11], "Symmetries of Culture" by D.K. Washburn & D.W. Crowe [12], etc.). Beginning with intuitively recognized regularities, and probably from very simple construction methods based on several basic (antisymmetric) prototiles (e.g., from Truchet tiles [13, 14] or similar elements), the historical development of antisymmetry ornaments proceeds by the use of modularity [15]. This is reason to believe that the theory of symmetry, literally taken from mathematical crystallography is probably not the only way, and maybe not the best explanation for the construction of ancient antisymmetric patterns. We believe that their basic concept and construction method was mostly derived from such usual working technologies, as matting, weaving, printing, and production of textiles or fabrics, rather then from the regular multiplication of a fundamental region by some (anti)symmetry group.

Antisymmetry introduced in ornamental art the possibility of expressing, in a symbolical sense, a dynamic conflict, duality, and illustrated alternating natural phenomena (day-night, tides, phases of the Moon, a change of seasons). Treating the color change "black-white" as a space property, a suggestion of "two-sidedness'’ (over-under, above-below) antisymmetry introduces also a 3D space component in ornamental art. This way, in both cases, as a kind of time component or space component, it introduces a new dimension, making possible a dimensional transition from a 2D plane image to 3-dimensionality. 

If we identify the color reversing transformation with reflection in the plane of the pattern, 2D antisymmetry groups of rosettes, friezes and plane ornaments are models of 3D symmetry groups of tablets, bands and layers, respectively. Exactly that idea was the origin of the mathematical theory of antisymmetry. Such visualization in a 2D plane, using black-white diagrams, was proposed in 1927 by A. Speiser, and presented by L.Weber in 1929 [16]. The black-white diagrams of bands from his paper (Fig. 1), where the alternation of colors is used to denote figures above and below the invariant plane of the pattern, suggested the possibility for a more general dimensional transition from the symmetry groups of n-dimensional space, using the antisymmetry groups, to the symmetry groups of (n+1)-dimensional space. That natural idea of a more sophisticated dimensional transition from 3D to 4D space resulted in one of the first and the most remarkable early results of H. Heesch [17] – the approximate number of four-dimensional groups preserving invariant 3D-space (less then 2000). The 1651 3D-space antisymmetry groups, modeling the mentioned four-dimensional groups, were derived for the first time more then 30 years later by A.M. Zamorzaev in 1953 [18]. Unfortunately, the work of H. Heesh published in a crystallographic journal, as well as the paper of H.J. Woods [19] giving the derivation of the 46 black-white symmetry groups of plane patterns, published in the Manchester Journal of the Textile Institute in 1935, never attracted the attention of readers they deserved. 

Figure 1: Weber diagrams of bands.

Later, in the 40's and 50's, A.V. Shubnikov [20], V.A. Koptsik and several other authors considered the possible applications of antisymmetry in crystallography, physics and other natural sciences. In their works, antisymmetry is mostly interpreted as an alternating change of some bivalent physical property (e.g., the electrical charge + and -, magnetic orientation S or N, etc.). 

The mathematical approach to antisymmetry has made possible the exact treatment of 7000 years old ornamental heritage, covering almost complete history of civilization, the classification and analysis of antisymmetric patterns, and the future non-empirical use of antisymmetry in ornamental art and design. For every antisymmetric pattern it is possible to recognize its antisymmetry group and classify it according to that symmetry property. 
 
 

Let a symmetry group G and the permutation group P=C₂ generated by the color-change transformation e₁=(0 1) (i.e., black-white) satisfying the relation e₁²=E and commuting with all elements of the group G, be given. If SÎ G, then S’=e₁S=Se₁ is the antisymmetry transformation derived from S. Each group G’ derived from G, which contains at least one antisymmetry transformation is called the antisymmetry group, and the group G is called its generating group. All antisymmetry groups derived from G may be divided into the two types: "gray" groups of the form G´ C₂ and "black-white" groups G’ isomorphic with G. Hence, it is clear that only second groups are non-trivial in the sense of derivation. Every black-white antisymmetry group G’ is uniquely defined by its group/subgroup symbol G/H, where H is the symmetry subgroup of G’, G/HC₂, and [G:H]=2. From that follows a very simple visual method for the recognition of antisymmetry groups in two steps: 

     (a) recognition of a symmetry group G of uncolored pattern; 

     (b) recognition of a color-preserving subgroup H of the two-colored pattern. 

For example, from the generating symmetry group D₄=4m (the symmetry group of a square) generated by rotation S of order 4 and reflection R, we obtain two black-white antisymmetry groups 4m’ generated by S and R’, and 4’m generated by S’ and R. In the first we recognize its color-preserving subgroup C₄=4, and in the other D₂=2m, so the first antisymmetry group can be denoted by the group/subgroup symbol D₄/C₄ = 4m/4, and the other by D₄/D₂ = 4m/2m (Fig. 2) [8, 21, 22]. The same antisymmetry groups will be obtained if we use rotation S and reflection R₁ in a diagonal as the generators of the group D₄=4m.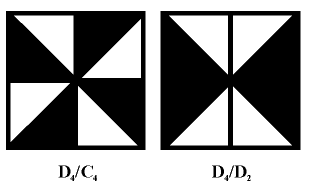

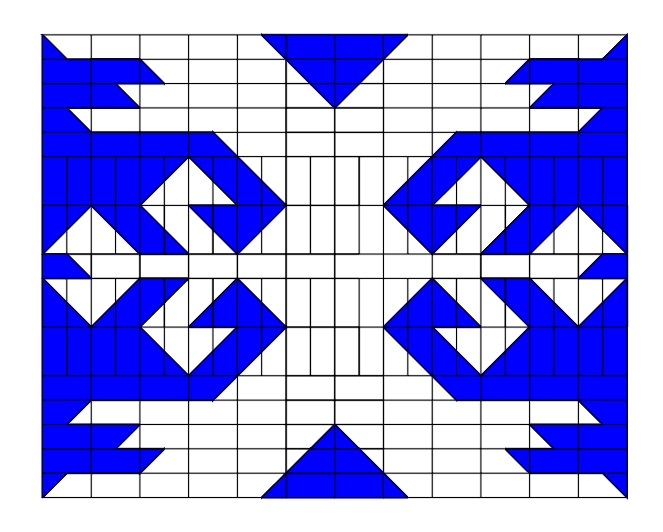
Figure 2: Antisymmetry desymmetrizations of D₄.

Regarded from the symmetry viewpoint, every regular coloring represents a desymmetrization (or "symmetry-breaking") of some symmetry group resulting in some of its subgroups. In the case of antisymmetry, the result is a subgroup of index 2.

Even in Neolithic ornamental art it is possible to find a lot of antisymmetric rosettes, as well as examples of most of the antisymmetry friezes (14 from 17) (Fig. 3) and ornaments (23 from 46) [23]. In ornamental art the use of color in the sense of regular coloring, i.e. antisymmetry and colored symmetry, opened a large unexplored field. Hence, in the history of ornamental art, we can consider the Neolithic as its earliest peak, a period in which after solving the basic technical and constructional problems, new possibilities for artistic research, imagination, variety of motifs and decorativeness were opened.

Figure 3: Neolithic antisymmetry friezes.
 
 

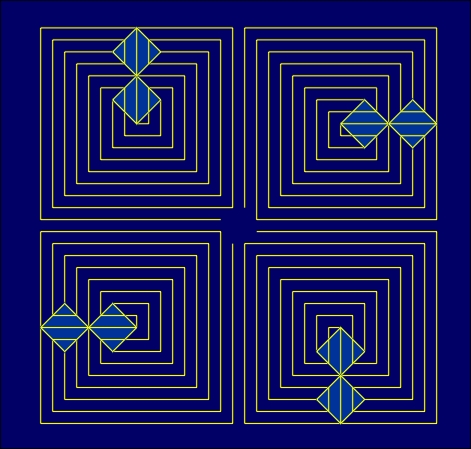
3. Symmetry vs. Modularity

It is interesting to notice that several rosettes and all mentioned 14 Neolithic antisymmetry friezes might be derived in a very simple way, using just one basic element: Truchet tile (black-white square in the lower right corner of Fig. 4) [13, 14] or a full set of tiles derived from a square by all its black-white colorings (Fig. 4). The same holds for a remarkable collection of antisymmetric patterns presented in one Cakaudrove cloth decoration, used as a cover of the book "Symmetry of Cultures" by D.K. Washburn and D.W. Crowe [12]. This indicates that artists and artisans in the Neolithic period, or in ethnic art, used a very restricted set of basic elements and their recombination. This is exactly the essence of the concept of modularity [15]. 

Modularity in art occurs when several basic elements (modules) are combined to create a large number of different (modular) structures. In art, different modules (e.g., bricks in architecture or in ornamental brickwork) occur as the basis of modular structures. In science, modularity is represented by a search for fundamental units and basic elements (e.g., physical constants, elementary particles, prototiles for different geometric structures, etc.). In various fields of (discrete) mathematics, the search for modularity is the recognition of sets of basic elements, construction rules and the exhaustive derivation of different generated structures.

In a general sense, modularity is a manifestation of the universal principle of economy in nature: the possibility for diversity and variability of structures, resulting from some (finite and very restricted) set of basic elements by their recombination. In all such cases, the most important step is the choice, by recognition or discovery, of the basic elements. This is illustrated by examples from ornamental art, where some elements originating from Paleolithic or Neolithic art are still present in ornamental art as "ornamental archetypes". One of them, discovered already in prehistory independently by different cultures distant in space and time, is the Truchet tile.

The other similar prototiles are obtained when some simple tile, a square, rectangle or triangle, is divided in 2 or more parts. From this division the full set of antisymmetry tiles is derived by a systematic coloring. If a basic tile is divided in n subregions, that complete set consists of 2ⁿ two-colored tiles. That method is used by A.M. Zamorzaev, A.F. Palistrant and other authors in order to visualize multiple antisymmetry groups by their mosaics [18]. A series of interesting ornaments of that kind was found in the authors’ attempts to make a symmetry reconstruction of the patterns from the kilims (carpets) from Pirot (Serbia, Yugoslavia) [24] or much older Turkish carpets [25]. In both cases we were able to recognize a simple set of two-colored rectangular or square elements (i.e., the complete set of antisymmetric prototiles) used as the modules (Figs. 5, 7).
 

In those patterns we can recognize a higher level of antisymmetry organization: instead of using a particular disjoint element arranged according to the laws of antisymmetry, here we have a complete counterchange – the perfect two-colored ornaments where the figure (black part) is congruent with the ground (white part), covering a plane without gaps or overlaps. This kind of ornament with zoomorphic counterchanging congruent tiles was created by M.C. Escher [9, 10], but a large number of such geometric ornaments can be found in the Neolithic ornamental art. In that sense, the patterns and the details from the kilims from Pirot or Turkish carpets could be considered as a treasure preserving some much older knowledge, originating even from prehistoric times. For example, some details from those carpets are very similar to parts of Neolithic ceramic ornaments from Hacilar (Fig. 6).

Figure 6: Antisymmetry ornament from Hacilar.

Figure 7: Rectangular black-white prototiles as a basis of antisymmetric pattern.

For Neolithic ceramic ornaments, this kind of a perfect counterchange is not an exception, but almost a rule. This can be shown by analyzing black-white patterns from the Neolithic of Hungary, Romania, Greece, and Yugoslavia. According to Nandor Kalicz [26], their common origin could be the Neolithic textiles, i.e., matting, which them the ornaments have been copied to the other stronger media (ceramic) (Figs. 8, 9).

The other prototile based on the antisymmetry and used abundantly in ornamental art, even from the time of the Paleolithic, was a square with a set of diagonal bands. Decomposing such a square into two squares (a "positive" and "negative") and arranging them in patterns by using very simple repetition or alternation rules (left, right, left, right, etc.), an infinite series of patterns can be obtained. These patterns, known as "key-patterns", are common for different cultures (Paleolithic, Neolithic, Chinese, Celtic) and were independently discovered by them. The oldest examples of key-patterns are ornaments from Mezin (Ukraine, about 23 000 B.C.) (Fig. 10) [27]. After that, their appearance in prehistoric ornamental art can be traced in archeological findings from Moldavia, Romania, Hungary, Yugoslavia, and Greece, and all of them can be derived as modular structures (Fig. 11). It is interesting that almost identical key-patterns can be found in widely separate parts of the world (e.g., in Hungary and in Fiji islands, as Lapita patterns, both in the ceramics from the Neolithic period) (Fig. 12). This could be considered as evidence that different cultures discovered the same basic elements and created even the similar or same ornaments by using modularity.

The same basic elements, "positive" and "negative" square with diagonals, is also preserved in another very ancient kind of art: in the art of mazes. That art, known from Greek mazes (labyrinth from Knossos), Roman mazes [28, 29], or Celtic mazes (Fig. 13) [30, 31], probably comes from much older, Neolithic or even Paleolithic origin.

Analyzing black-white ornaments occurring in history, at first glance, it seems as though the simplest method for their construction might be the use of symmetry laws: a multiplication of a fundamental region of some symmetry group by antisymmerries, a multiplication of asymmetrical figure, or alternating black-white coloring of some isohedral tiling. In any case, applying just symmetry, for some of them it is very difficult to comprehend how they are constructed and how the regularities are so strictly respected by ancient artists and artisans. In some cases, the answer can be found in modularity, where the construction of complex structures (or at least structures that look as complicated) is reduced to the use of several basic elements (modules) that are sometimes symmetrical, and that are multiplied by a very simple algorithmic rule. Let us mention that certain complex structures (e.g., fractals) can be described by very simple iterative formulas. In the case of modularity, the most important is the choice of modules that by themselves represent some kind of "semi-gestalts": they are very compact, self-contained and simple, but on the other hand, they are building blocks for diverse complex structures.
 
 

[1] M. Ghyka, Philosophie et mistique du nombre, Éd. Payot, Paris, 1971.

[2] A. Speiser, Die Theorie der Gruppen von endlicher Ordnung, 2nd ed., Springer, Berlin, 1927.

[3] E. Müller, Gruppentheoretische und Strukturanalytische Untersuchungen der Maurischen Ornamente aus der Alhambra in Granada, Ph.D. Thesis, Univ. Zürich, Rüschlikon, 1944.

[4] A.O. Shepard, The Symmetry of Abstract Design with Special Reference to Ceramic Decoration, Carnegie Inst. of Washington, Publ. No. 575, Washington DC, 1948.

[5] H. Weyl, Symmetry, Princeton University Press, Princeton, 1952.

[6] D.K. Washburn, Symmetry Analysis of Ceramic Design: Two Tests of the Method on Neolithic Material from Greece and the Aegean, In Structure and Cognition in Art, Cambridge University Press, London, 1983.

[7] D.K. Washburn, A Symmetry Analysis of Upper Gila Area Ceramic Design Decoration, Carnegie Inst., Washington DC, 1977.

[8] S. Jablan, Theory of Symmetry and Ornament, Matematicki institut, Beograd, 1995.

[9] C.H. Macgillavry, Fantasy and Symmetry, The Periodic Drawings of M.C.Escher, New York, 1972.

[10] D. Schattschneider, Visions of Symmetry : Notebooks, Periodic Drawings, and Related Work of M.C. Escher,  W.H. Freeman, San Francisco, 1992. 

[11] A.V. Shubnikov, V.A. Koptsik, Symmetry in Science and Art, Plenum Press, 1972.

[12] D.K. Washburn, D.W. Crowe, Symmetries of Culture, Theory and Practice of Plane Pattern Analysis, University of Washington Press, Washington, 1988.

[13] E.H. Gombrich, Sense of Order, Phaidon Press, London, 1979.

[14] D.E. Smith, The Tiling Patterns of Sebastien Truchet and the Topology of Structural Hierarchy, Leonardo 20, 4 (1987) 373-385.

[15] S. Jablan, Modularity in Art, http://members.tripod.com/modularity/

[16] L. Weber, Die Symmetrie homogener ebener Punktsysteme, Z. Krist., 70 (1929), 309-327.

[17] H. Heesch, Über der vierdimensionalen Gruppen des Dreidimensionalen Raums, Z. Krist., 73 (1930), 325-345.

[18] A.M. Zamorzaev, Teoriya prostoi i kratnoi antisimmetrii, Shtiintsa, Kishinev, 1976. 

[19] H.J. Woods, The geometrical basis of pattern design, J. Text. Inst., 26 (1935), 197-293.

[20] A.V. Shubnikov, N.V. Belov at all., Colored Symmetry, Pergamon, Oxford, London, New York, Paris, 1964.

[21] S.Jablan, Teorija proste i visestruke antisimetrije u E² i E²\{O}, Ph. D. Dissertation, Prirodno-matematicki fakultet, Beograd, 1984.

[22] Lj. Radovic, Antisimetrija i visestruka antisimetrija, M.A. Dissertation, Univerzitet u Nisu, 2000.

[23] S. Jablan, Symmetry and Ornament, Bridges: Mathematical Connections in Art, Music and Science, Conference Proceedings 2000, 1-13.

[24] M. Zivkovic, Album pirotskih cilimova, Tesen (Austrija), 1902.

[25] G. Erbek, Kilim: Catalogue No. 1, Selçuk A.S., Istambul, 1990.

[26] N. Kalicz, Die Gotter aus Ton, Corvina Verlag, Budapest, 1989.

[27] M. Gimbutas, The Language of the Goddess, Harper & Row, San Francisco, 1989.

[28] A. Phillips, The Topology of Roman Mazes, Leonardo : Visual Mathematics 25, 3-4 (1992), 321-329.

[29] W.H. Mathews, Mazes & Labyrinths: their History and Development, Dover, New York, 1970.

[30] G. Bain, Celtic Art - the Methods of Construction, Dover, New York, 1973.

[31] A. Meehan, Maze Patterns, Thames and Hudson, New York, 1993.